Temat: OBIEKT DYNAMICZNY LINIOWY

1. Badanie podstawowych członów dynamicznych

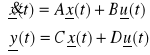
1. Proporcjonalny

,
,
,
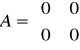
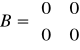
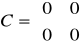
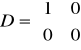
•(-1) →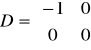

przykładowe równanie ma postać: y = kp•u

2. Całkujący

,
,
,

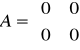
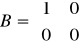
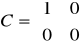
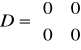
przykładowe równania układu mają postać: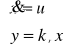

3. Inercyjny

,
,
,

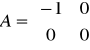
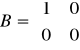
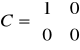
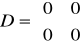
przykładowe równania układu mają postać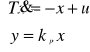

4. Różniczkujący rzeczywisty

,
,
,

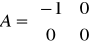
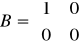
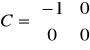
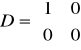
przykładowe równania układu mają postać:

5. Proporcjonalno - całkujący

,
,
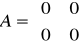
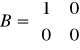
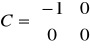
•(-1)→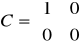
,

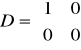
•(-1)→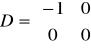

przykładowe równania układu mają postać: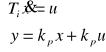

6. Dwuinercyjny

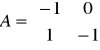
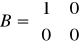
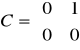
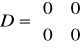
przykładowe równania układu mają postać: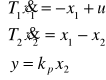

7. Oscylacyjne

przykładowe równania układu mają postać: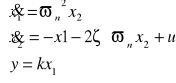

,
,
,

,
,
,
,

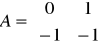
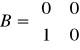
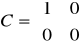
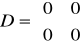
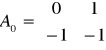
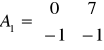
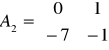
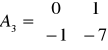
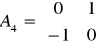
2. Badanie prostego układu regulacji

1. Obliczenia transmitancji dwóch elementów (inercyjnego i całkującego) połączonych szeregowo (k₁=k₂=1; T=1):

2. Obliczenia transmitancji wypadkowej z uwzględnieniem sprzężenia zwrotnego:

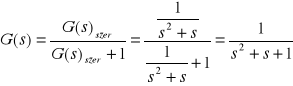
3. Po uwzględnieniu definicji transmitancji ( G(s) = Y(s)/U(s) ), transmitancja wypadkowa wyraża się następująco:

4. na podstawie powyższego wyrażenia można utworzyć równania stanu i wyjść obiektu dynamicznego

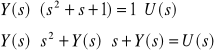
Po przejściu do dziedziny czasu otrzymujemy:

otrzymane równanie jest równaniem różniczkowym 2-go rzędu, zatem można utworzyć 2 równania różniczkowe 1-go rzędu, które odpowiadać będą dwóm równaniom stanu. Jako zmienną stanu dobieramy sygnał wyjściowy y(t) wtedy zgodnie z zasadami doboru zmiennych fazowych można utworzyć relacje: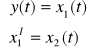

zatem równania obiektu dynamicznego są następujące: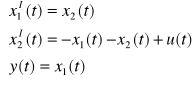
macierze odnoszące się do powyższego układu równań są następujące:

macierz stanu: macierz wejść: macierz wyjść: macierz transmisyjna

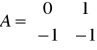
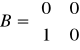
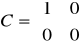
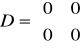
Można zauważyć, że macierz transmitancji jest zerowa, więc nie ma oddziaływania z wejścia na wyjście.

5. Sprawdzam czy powyższy układ jest sterowalny

• warunkiem koniecznym i dostatecznym sterowalności jest aby macierz S=[B, AB, A²B,...,A^n-1B] była rzędu n (czyli żeby miała n liniowo niezależnych kolumn).

• Układ, którego sterowalność będę sprawdzał jest układem z jednym wejściem u(t)=u(t), czyli równanie stanu ma postać
  

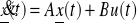
• układ z jednym wejściem jest sterowalny jeśli:

det S=[b,Ab, A²b,...,A^n-1b]≠0

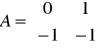
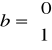
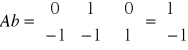
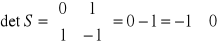
W macierzy S występują dwie niezależne liniowo kolumny, a wyznacznik jest różny od zera czyli układ jest sterowalny.

1. Sprawdzam czy powyższy układ jest obserwowalny.

• warunkiem koniecznym i dostatecznym obserwowalności jest, aby macierz W=[C^T, A^TC^T, (A^T)²C^T, ..., (A^T)^n-1C^T] była rzędu n (czyli miała n-liniowo niezależnych kolumn.

• Układ którego obserwowalność będziemy sprawdzać jest układem o jednym wyjściu y(t)=y(t), czyli równanie wyjścia ma postać: y(t)=cx(t), czyli warunkiem koniecznym i wystarczającym jest aby macierz W nie była osobliwa, czyli det.W≠0.

,
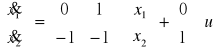
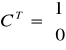
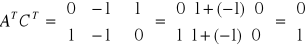
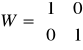
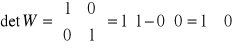
czyli układ jest obserwowalny

1. Sprawdzam czy powyższy układ jest stabilny (kryterium Hurwiza).

Aby wszystkie pierwiastki równania charakterystycznego

U(s)=0

miały części rzeczywiste ujemne, muszą być spełnione następujące warunki:

• wszystkie współczynniki równania istnieją i są większe od zera (jest to warunek konieczny, ale nie dostateczny).

Współczynniki równania istnieją i są większe od zera, czyli : a₁=1>0; a₂=1>0; a₀=1>0. Warunek spełniony.

• wszystkie podwyznaczniki wyznacznika głównego [R] istnieją i są większe od zera

W(s)= s²+s+1 → a₂•s² + a₁•s + a₀=0

a₀ = 1, a₁ = 1, a₂ = 1

a>0

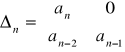
; n=2

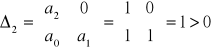
Układ jest stabilny wg kryterium Hurwitza, gdyż spełnione są powyższe warunki: równanie charakterystyczne ma wszystkie pierwiastki o ujemnej części rzeczywistej, gdyż spełnione są powyższe warunki. Tak więc koniecznym i dostatecznym warunkiem stabilności układu jest aby pierwiastki równania charakterystycznego układu zamkniętego miały ujemne części rzeczywiste.

Wnioski

Układ dynamiczny to dowolny układ fizyczny, rozpatrywany z punktu widzenia jego zachowania się w czasie. Otrzymane w trakcie ćwiczenia przebiegi z badanych układów dostarczają nam informacji o stanie układu. Znając transmitancję układu można wyznaczyć odpowiedź Y(t) układu przy dowolnym wymuszeniu U(t).

W pierwszej części ćwiczenia badano różne człony dynamiczne modelując odpowiednio macierze A, B, C i D na stanowisku badawczym. Wszystkie charaktery­styki skokowe otrzymane podczas badań są zgodne z charakterystykami teoretycz­nymi.

Badanie każdego elementu dynamicznego przeprowadzono dla różnych wymuszeń. Dla członu oscylacyjnego dokonano kilku zmian pa­rametrów macierzy A, przez co uzyskaliśmy kilka różnych charakterystyk skokowych o różnych tłumieniach.

Z analizy członów oscylacyjnych, wywnioskowano, że kolejne elementy macierzy A powodują (przy zwiększaniu ich wartości): wzrost amplitudy, częstotliwości odpowiedzi tłumienie wykresu odpowiedzi do zera oraz tłumienie oscylacji.

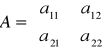
a₁₁ - nie ma wpływu, wartość wynosi 0

a₁₂ - ulega zmianie amplituda i częstotliwość oscylacji,

a₂₁ - tłumi wykres odpowiedzi do zera, ulega zmianie współczynnik wzmocnienia, amplituda i częstotliwość. Zauważono, że zwiększając a₂₁ amplituda, częstotliwość ulegają zmniejszeniu.

a₂₂ - przy zwiększeniu wartości rośnie tłumienie, likwiduje oscylacje.

Kolejnym etapem było badanie prostego układu regulacji. Po sprawdzeniu warunków sterowalności, obserwowalności i stabilności okazało się, że układ jest sterowalny i obserwowalny oraz stabilny.

---