Analiza notowań akcji „Dębica” w okresie od 06.03.01r. do 03.05.01r.
Data |
t |
Notowania „Dębica“ |
06.03.01 |
1 |
26,13 |
08.03.01 |
2 |
25,88 |
10.03.01 |
3 |
25,82 |
12.03.01 |
4 |
27,70 |
14.03.01 |
5 |
25,20 |
16.03.01 |
6 |
26,05 |
18.03.01 |
7 |
25,80 |
20.03.01 |
8 |
25,10 |
22.03.01 |
9 |
24,93 |
24.03.01 |
10 |
25,02 |
26.03.01 |
11 |
25,85 |
28.03.01 |
12 |
25,15 |
28.12.00 |
13 |
25,80 |
30.03.01 |
14 |
25,08 |
01.04.01 |
15 |
26,00 |
03.04.01 |
16 |
25,03 |
05.04.01 |
17 |
24,94 |
07.04.01 |
18 |
25,90 |
09.04.01 |
19 |
25,01 |
11.04.01 |
20 |
24,90 |
13.04.01 |
21 |
24,87 |
15.04.01 |
22 |
25,00 |
17.04.01 |
23 |
24,75 |
19.04.01 |
24 |
25,18 |
21.04.01 |
25 |
24,90 |
23.04.01 |
26 |
25,02 |
25.04.01 |
27 |
25,15 |
27.04.01 |
28 |
25,98 |
29.04.01 |
29 |
28,06 |
01.05.01 |
30 |
25,08 |
Suma |
465 |
762,28 |
Na podstawie informacji o notowaniach akcji „Dębica” w ciągu poszczególnych dni i graficznej prezentacji danych możliwe jest wyciągnięcie pierwszych wniosków i ocena właściwości szeregu.
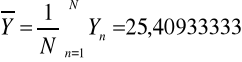
Średnia arytmetyczna:
Bazując na drugim wykresie można łatwo zauważyć, jak przebiega przybliżona linia trendu. Jest ona opadająca w ciągu całego badanego okresu, co oznacza, że kurs EURO spada.
Szukamy linii trendu:
gdzie
Kryterium weryfikacji modelu
Aby wyznaczyć parametry prostej, dla której suma kwadratów reszt jest najmniejsza, korzystamy z warunków koniecznych istnienia ekstremum.
Funkcja będąca kryterium jest dodatnio określoną formą kwadratową ze względu na α1 i α2. Osiąga zatem minimum w punkcie, w którym zerują się pierwsze pochodne.
Warunek konieczny istnienia ekstremum:
Warunek istnienia rozwiązania:
W = 67425
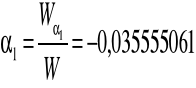
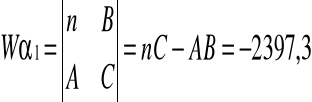
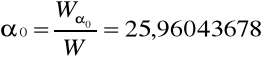
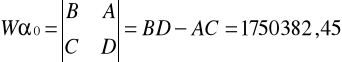
Parametry równania trendu:
Równanie trendu:
![]()
Natomiast reszta wynosi:
![]()
Otrzymany proces E(t) stanowiący różnicę pomiędzy procesem podstawowym i linią trendu należy zbadać przy pomocy funkcji autokorelacji.
Identyfikacja modelu AR.
Zakładamy, że obserwowany proces będzie opisany modelem autoregresji rzędu II.
AR(2)
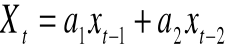
Kryterium identyfikacji modelu
Warunek konieczny istnienia ekstremum
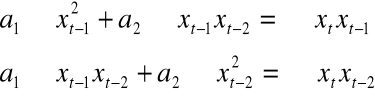
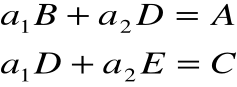
Warunek istnienia rozwiązania:
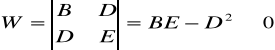
Obliczenie wartości parametrów a1 i a2 z wyznaczników:
W = 12022874,7
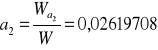
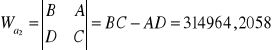
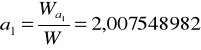
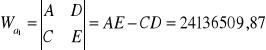
Model autoregresji rzędu II dopasowany do analizowanych danych, a więc obrazujący wahania notowań akcji „Dębica”, ma postać:
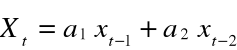
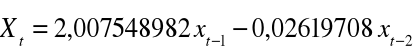
Należy zbadać wzajemną korelację pomiędzy wyrazami reszt. Do tego celu służy funkcja autokorelacji.
Funkcja autokorelacji wyraża się wzorem:
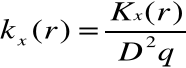
Nie unormowana funkcja autokorelacji jest kowariancją (estymatorem kowariancji) procesu Et. Wyraża się wzorem:
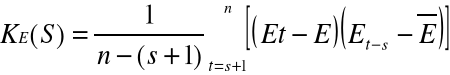
![]()
Funkcja autokorelacji w zerze:
![]()
Wyliczono 7 kroków funkcji autokorelacji:
K(0)= 0,3833099
K(1)= 0,0516081 k(1)= 1
K(2)= 0,1295202 k(2)= 2,509688707
K(3)= 0,1289958 k(3)= 2,499528131
K(4)= 0,0332215 k(4)= 0,64727286
K(5)= 0,0032891 k(5)= 0,063731767
K(6)= -0,0333456 k(6)= -0,646131838
K(7)= 0,0574156 k(7)= 1,112531543
Reszty nie stanowią „białego szumu”. Może to oznaczać, że reszty można modelować lub że należy przyjąć inny model dla procesu podstawowego.
Projekt
z
ekonometrii
nr 3
TEMAT:
Analiza szeregu czasowego
Obliczenia pomocnicze do wyznaczenia linii trendu:
t |
Xt |
t*Xt |
t^2 |
X^(t) |
E(t) |
1 |
26,13 zł |
26,13 |
1 |
25,92488172 |
0,20511828 |
2 |
25,88 zł |
51,76 |
4 |
25,88932666 |
-0,009326659 |
3 |
25,82 zł |
77,46 |
9 |
25,8537716 |
-0,033771598 |
4 |
27,70 zł |
110,8 |
16 |
25,81821654 |
1,881783463 |
5 |
25,20 zł |
126 |
25 |
25,78266148 |
-0,582661476 |
6 |
26,05 zł |
156,3 |
36 |
25,74710641 |
0,302893585 |
7 |
25,80 zł |
180,6 |
49 |
25,71155135 |
0,088448647 |
8 |
25,10 zł |
200,8 |
64 |
25,67599629 |
-0,575996292 |
9 |
24,93 zł |
224,37 |
81 |
25,64044123 |
-0,710441231 |
10 |
25,02 zł |
250,2 |
100 |
25,60488617 |
-0,58488617 |
11 |
25,85 zł |
284,35 |
121 |
25,56933111 |
0,280668891 |
12 |
25,15 zł |
301,8 |
144 |
25,53377605 |
-0,383776047 |
13 |
25,80 zł |
335,4 |
169 |
25,49822099 |
0,301779014 |
14 |
25,08 zł |
351,12 |
196 |
25,46266593 |
-0,382665925 |
15 |
26,00 zł |
390 |
225 |
25,42711086 |
0,572889136 |
16 |
25,03 zł |
400,48 |
256 |
25,3915558 |
-0,361555803 |
17 |
24,94 zł |
423,98 |
289 |
25,35600074 |
-0,416000742 |
18 |
25,90 zł |
466,2 |
324 |
25,32044568 |
0,57955432 |
19 |
25,01 zł |
475,19 |
361 |
25,28489062 |
-0,274890619 |
20 |
24,90 zł |
498 |
400 |
25,24933556 |
-0,349335558 |
21 |
24,87 zł |
522,27 |
441 |
25,2137805 |
-0,343780497 |
22 |
25,00 zł |
550 |
484 |
25,17822544 |
-0,178225436 |
23 |
24,75 zł |
569,25 |
529 |
25,14267037 |
-0,392670374 |
24 |
25,18 zł |
604,32 |
576 |
25,10711531 |
0,072884687 |
25 |
24,90 zł |
622,5 |
625 |
25,07156025 |
-0,171560252 |
26 |
25,02 zł |
650,52 |
676 |
25,03600519 |
-0,016005191 |
27 |
25,15 zł |
679,05 |
729 |
25,00045013 |
0,14954987 |
28 |
25,98 zł |
727,44 |
784 |
24,96489507 |
1,015104931 |
29 |
25,06 zł |
726,74 |
841 |
24,92934001 |
0,130659993 |
30 |
25,08 zł |
752,4 |
900 |
24,89378495 |
0,186215054 |
465 |
762,28 |
11735,43 |
9455 |
762,28 |
2,4869E-13 |
Obliczenia pomocnicze wykorzystane do prezentacji modelu autoregresji rzędu II:
t |
Xt |
Xt-1 |
Xt-2 |
1 |
26,13 zł |
|
|
2 |
25,88 zł |
26,13 |
|
3 |
25,82 zł |
25,88 |
26,13 |
4 |
27,70 zł |
25,82 |
25,88 |
5 |
25,20 zł |
27,70 |
25,82 |
6 |
26,05 zł |
25,20 |
27,70 |
7 |
25,80 zł |
26,05 |
25,20 |
8 |
25,10 zł |
25,80 |
26,05 |
9 |
24,93 zł |
25,10 |
25,80 |
10 |
25,02 zł |
24,93 |
25,10 |
11 |
25,85 zł |
25,02 |
24,93 |
12 |
25,15 zł |
25,85 |
25,02 |
13 |
25,80 zł |
25,15 |
25,85 |
14 |
25,08 zł |
25,80 |
25,15 |
15 |
26,00 zł |
25,08 |
25,80 |
16 |
25,03 zł |
26,00 |
25,08 |
17 |
24,94 zł |
25,03 |
26,00 |
18 |
25,90 zł |
24,94 |
25,03 |
19 |
25,01 zł |
25,90 |
24,94 |
20 |
24,90 zł |
25,01 |
25,90 |
21 |
24,87 zł |
24,90 |
25,01 |
22 |
25,00 zł |
24,87 |
24,90 |
23 |
24,75 zł |
25,00 |
24,87 |
24 |
25,18 zł |
24,75 |
25,00 |
25 |
24,90 zł |
25,18 |
24,75 |
26 |
25,02 zł |
24,90 |
25,18 |
27 |
25,15 zł |
25,02 |
24,90 |
28 |
25,98 zł |
25,15 |
25,02 |
29 |
25,06 zł |
25,98 |
25,15 |
30 |
25,08 zł |
25,06 |
25,98 |
|
762,28 zł |
737,2 |
712,14 |
cd. obliczeń:
Xt*Xt-1 |
Xt-12 |
Xt*Xt-2 |
Xt-1*Xt-2 |
Xt-22 |
Xt^=a1*Xt-1+a2*Xt-2 |
Xt-Xt^ |
|
|
|
|
|
|
|
676,24 |
682,78 |
|
|
|
676,24 |
682,78 |
668,22 |
669,77 |
674,68 |
676,24 |
682,78 |
668,22 |
669,77 |
715,21 |
666,67 |
716,88 |
668,22 |
669,77 |
715,21 |
666,67 |
698,04 |
767,29 |
650,66 |
715,21 |
666,67 |
698,04 |
767,29 |
656,46 |
635,04 |
721,59 |
698,04 |
767,29 |
656,46 |
635,04 |
672,09 |
678,60 |
650,16 |
656,46 |
635,04 |
672,09 |
678,60 |
647,58 |
665,64 |
653,86 |
672,09 |
678,60 |
647,58 |
665,64 |
625,74 |
630,01 |
643,19 |
647,58 |
665,64 |
625,74 |
630,01 |
623,75 |
621,50 |
628,00 |
625,74 |
630,01 |
623,75 |
621,50 |
646,77 |
626,00 |
644,44 |
623,75 |
621,50 |
646,77 |
626,00 |
650,13 |
668,22 |
629,25 |
646,77 |
626,00 |
650,13 |
668,22 |
648,87 |
632,52 |
666,93 |
650,13 |
668,22 |
648,87 |
632,52 |
647,06 |
665,64 |
630,76 |
648,87 |
632,52 |
647,06 |
665,64 |
652,08 |
629,01 |
670,80 |
647,06 |
665,64 |
652,08 |
629,01 |
650,78 |
676,00 |
627,75 |
652,08 |
629,01 |
650,78 |
676,00 |
624,25 |
626,50 |
648,44 |
650,78 |
676,00 |
624,25 |
626,50 |
645,95 |
622,00 |
648,28 |
624,25 |
626,50 |
645,95 |
622,00 |
647,76 |
670,81 |
623,75 |
645,95 |
622,00 |
647,76 |
670,81 |
622,75 |
625,50 |
644,91 |
647,76 |
670,81 |
622,75 |
625,50 |
619,26 |
620,01 |
622,00 |
622,75 |
625,50 |
619,26 |
620,01 |
621,75 |
618,52 |
622,50 |
619,26 |
620,01 |
621,75 |
618,52 |
618,75 |
625,00 |
615,53 |
621,75 |
618,52 |
618,75 |
625,00 |
623,21 |
612,56 |
629,50 |
618,75 |
625,00 |
623,21 |
612,56 |
626,98 |
634,03 |
616,28 |
623,21 |
612,56 |
626,98 |
634,03 |
623,00 |
620,01 |
630,00 |
626,98 |
634,03 |
623,00 |
620,01 |
629,25 |
626,00 |
626,24 |
623,00 |
620,01 |
629,25 |
626,00 |
653,40 |
632,52 |
650,02 |
629,25 |
626,00 |
653,40 |
632,52 |
651,06 |
674,96 |
630,26 |
653,40 |
632,52 |
651,06 |
674,96 |
628,50 |
628,00 |
651,58 |
651,06 |
674,96 |
628,50 |
628,00 |
18714,8939 |
18751,1362 |
18068,2287 |
18086,3891 |
18123,1326 |
18714,8939 |
18751,1362 |
![]()
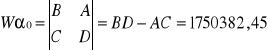
![]()
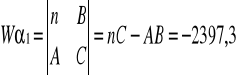
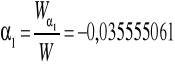
![]()
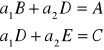
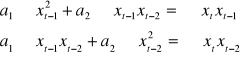
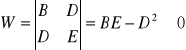
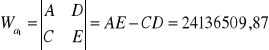
![]()
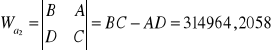
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka