Opracowanie wyników.

1. Obliczamy średnią długość średnicy kuli:

d_śr =28,32 mm

Δd =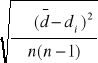

Δd=0,00003 m

(d= 0,02832 ± 0,00003 m)

2. Obliczamy okresy wahań dla kolejnych pomiarów:

T₁ = 7.80/5 = 1,56 [s] (T₁)² = 2.43 [s²]

T₂ = 7.32/5 = 1.46 [s] (T₂)² = 2.13 [s²]

T₃ = 6.72/5 = 1.34 [s] (T₃)² = 1.79 [s²]

T₄ = 5.94/5 = 1.18 [s] (T₄)² = 1.39 [s²]

T₅ = 4.98/5 = 0.99 [s] (T₅)² = 0.992 [s²]

T₆ = 3.88/5 = 0.77 [s] (T₆)² = 0.602 [s²]

3. Obliczamy l ze wzoru l = l'+ 0,5 d

l₁ = 0,64+0,5*0,02832=0,654 [m]

l₂ = 0,54+0,5*0,02832=0,554 [m]

l₃ = 0,44+0,5*0,02832=0,45 [m]

l₄ =0,34+0,5*0,02832=0,354 [m]

l₅ =0,24+0,5*0,02832=0,254 [m]

l₆ =0,14+0,5*0,02832=0,154 [m]

4. Metodą regresji liniowej wyznaczamy nachylenie prostej A_{m :}

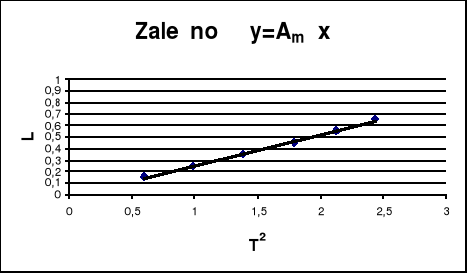
y = A_m * x , y=l , x= T² , A_m = a

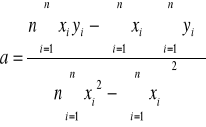
a = 6*4,412-2,42*9,33/6*16,91-87,05 = 3,892/14,41 = 0,27

A_m = 0,27

Obliczamy niepewność pomiarową
, najpierw musimy wyznaczyć wartość b, stosując wzór :

b
, czyli :

b = 1/6 * (2,42-2,5191) = 1/6 * (-0,0099) =

= -0,00165

Mając wyznaczoną wartość b obliczamy niepewność pomiarową
, korzystając z równania :

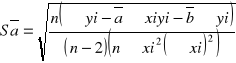
gdzie
to szukana niepewność
. Po podstawieniu danych do powyższego wzoru otrzymujemy:

ΔA_m = 0,008.

5. Korzystając z wyznaczonej wielkości A_m oraz ΔA_m obliczamy g oraz Δg:

g = 4Π²* A_m

g = 10,65[m/s²]

Korzystając z ΔA_m obliczamy Δg Δg =4Π² ×ΔA_m

Δg = 0,35 [m/s²]

Porównanie z wartościami tablicowymi:

Otrzymana wartość :10,65 [m/s²]

Tablicowa wartość : 9,81[m/s²]

PODSUMOWANIE:

Błąd wyznaczenia przyspieszenia ziemskiego może wynikać z niedokładnego pomiaru czasu

wahnięć wahadła spowodowanego ułomnością zmysłów (chodzi o prawdopodobne zbyt późne włączanie i wyłączanie sekundomierza ).

2

1

---