Niech K - krzywa regularna o początku A i końcu B, zawarta w ![]()
Całka krzywoliniowa skierowana
(całka krzywoliniowa funkcji wektorowej)
Niech K - krzywa regularna o początku A i końcu B, zawarta w ![]()
W - pole wektorowe, ![]()
![]()
![]()
Wtedy
dzielimy krzywą K na n krzywych punktami: ![]()
, gdzie ![]()
dla i=1,2,…,n
tworzymy wektory cięciw: ![]()
dla ![]()
wybieramy po jednym punkcie ![]()
na każdej z krzywych cząstkowych ![]()
, ![]()
dla i=1,2,…,n
wyznaczamy wektory ![]()
dla i=1,2,…,n
tworzymy sumę ![]()
, gdzie „![]()
” oznacza iloczyn skalarny wektorów.
Definicja
Jeśli przy ![]()
i ![]()
istnieje granica ![]()
niezależna od sposobu podziału krzywej i od wyboru punktów Mi, to granicę tę nazywamy całką krzywoliniową skierowaną funkcji W wzdłuż krzywej K i oznaczamy
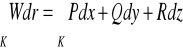
.
Uwagi
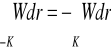
Jeśli krzywa ![]()
, jest zadana układem 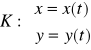
, ![]()
, a na krzywej K zadane jest płaskie pole wektorowe W o składowych [P,Q], to wtedy podobnie definiujemy całkę krzywoliniową skierowaną i oznaczamy ją
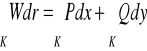
.
Jeśli ![]()
, gdzie ![]()
jest krzywą regularną dla i=1,…,n,
to definiujemy
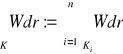
.
Twierdzenie (o zamianie całki krzywoliniowej skierowanej na całkę oznaczoną)
Niech K - krzywa regularna,
W - pole wektorowe ciągłe na krzywej ![]()
Wtedy
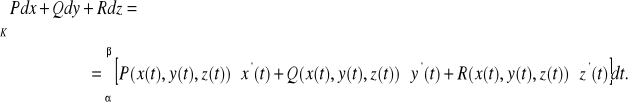
Uwaga
Jeśli krzywa K jest płaska, to
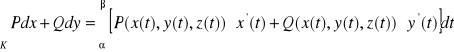
.
Interpretacja fizyczna
Niech K - krzywa skierowana od A do B,
W - pole sił na krzywej K.
Wtedy
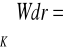
praca siły W wykonana przy przemieszczaniu masy jednostkowej wzdłuż krzywej K od punktu A do B.
Przykład (*)
Obliczyć całkę ![]()
po krzywej ![]()
skierowanej ujemnie względem swego wnętrza.
Zapiszmy równanie określające krzywą K w postaci równoważnej 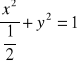
.
Jest to równanie elipsy.
Parametryzacja tej elipsy
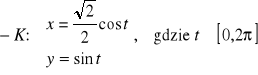
jest niezgodna z kierunkiem krzywej. Zatem
![]()
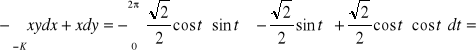
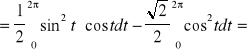
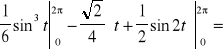
![]()
Definicja
Obszar płaski ograniczony jedną krzywą (Jordana) nazywamy jednospójnym, a obszar ograniczony p nieprzecinającymi się krzywymi obszarem p-spójnym.
obszar jednospójny obszar p-spójny
Umowa
Całkę krzywoliniową skierowaną po krzywej zamkniętej K oznaczamy też ![]()
.
Twierdzenie Greena
Z: Niech K - krzywa płaska zamknięta zorientowana dodatnio i ograniczająca obszar
jednospójny D,
P, Q - funkcje ciągłe mające ciągłe pochodne cząstkowe w obszarze D i na brzegu K.
T: 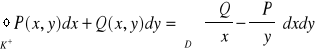
Przykład (*) c.d.
![]()
jest krzywą zorientowaną ujemnie, ![]()
,
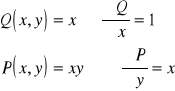
i z twierdzenia Greena otrzymujemy
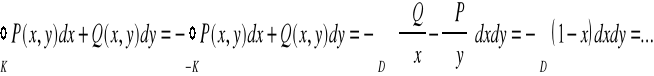
Zastosujemy uogólnione współrzędne biegunowe
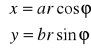
, gdzie a, b - stałe, ![]()
, ![]()
Jakobian powyższego odwzorowania wynosi![]()
.
W naszym przypadku wybieramy ![]()
, aby otrzymać obszar D ograniczony elipsą 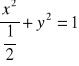
.Stąd
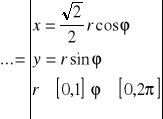
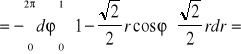
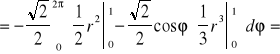
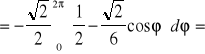
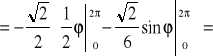
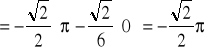
Twierdzenie (o niezależności całki krzywoliniowej od kształtu drogi całkowanej)
Z: Niech D - obszar jednospójny
P, Q - funkcje ciągłe, mające ciągłe pochodne cząstkowe w obszarze D
![]()
![]()
- krzywa regularna , ![]()
T: ![]()
- nie zleży od kształtu krzywej ![]()
a tylko od punktów A i B, t i wtedy oznaczamy ją 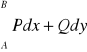
.
Dowód![]()
Niech ![]()
będą krzywymi regularnymi zawartymi w obszarze D, łączącymi punkty A i B, i skierowanymi od punktu A do B.
Wtedy krzywa ![]()
jest krzywą zamkniętą regularną, zorientowaną dodatnio, ![]()
. Oznaczmy przez ![]()
obszar jednospójny ograniczony przez krzywą C. Na podstawie twierdzenia Greena mamy
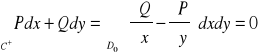
bo ![]()
, więc
![]()
![]()
![]()
![]()
Aby udowodnić implikację ![]()
wystarczy wykazać jej kontrapozycję, czyli udowodnić implikację
![]()
zależy od kształtu krzywej ![]()
.
Bez straty ogólności możemy założyć, że
![]()
.
Zatem
![]()
dla ![]()
.
Niech ![]()
będzie brzegiem koła ![]()
skierowanym dodatnio.
Wtedy na podstawie twierdzenia Greena mamy
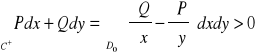
.
Stąd
![]()
,
czyli
![]()
.
Zatem całka po krzywej łączącej punkty A i B zależy od kształtu tej krzywej.
Wniosek
Niech D - obszar jednospójny,
C - krzywa zamknięta regularna, ![]()
,
![]()
- funkcje ciągłe mające ciągłe pochodne cząstkowe w D.
Wtedy
![]()
.
1
6