Pomiary:
T [°C] |
h1[mm Hg] |
h2[mm Hg] |
p =h1-h2 |
T [K] |
1/T |
ln(p/p0) |
30 |
15,85 |
11,10 |
4,75 |
303 |
0,003300 |
-5,08 |
32 |
16,10 |
11,00 |
5,10 |
305 |
0,003279 |
-5,00 |
34 |
16,35 |
10,90 |
5,45 |
307 |
0,003257 |
-4,94 |
36 |
16,60 |
10,60 |
6,00 |
309 |
0,003236 |
-4,84 |
38 |
16,80 |
10,40 |
6,40 |
311 |
0,003215 |
-4,78 |
40 |
17,00 |
10,10 |
6,90 |
313 |
0,003195 |
-4,70 |
Obliczenia przy p0 =760 mmHg.
T [°C] - temperatura otoczenia w °C,
h1 - wysokość słupka rtęci w lewym ramieniu tensometru,
h2 - wysokość słupka rtęci w prawym ramieniu tensometru,
T [K] - temperatura otoczenia w K,
p - wartość wyliczona ze wzoru p=h1-h2,
ln(p/p0) -wartość potrzebna do wykonania wykresu zależności ln(p/p0) = f(1/T),
Wykres zależności ln(p/p0) = f(1/T):
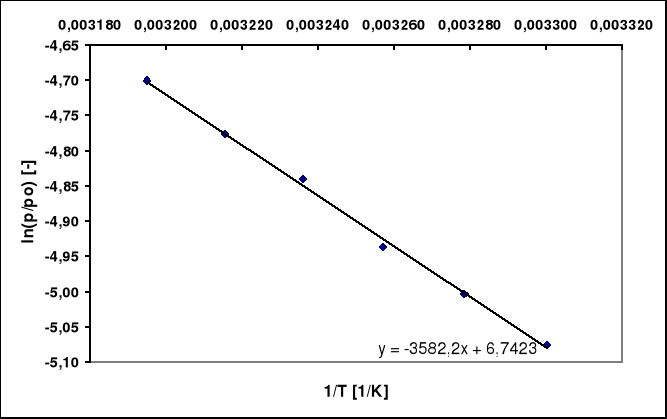
Wnioski:
Celem mojego doświadczenia było oznaczenie ciepła parowania za pomocą tensometru. Ze wzrostem temperatury słupek rtęci h1 rósł w górę, zaś drugi słupek h2 malał w dół. Zależność
ln(p/p0) = f(1/T) jest liniowa, a współczynnik kierunkowy jest liczbą ujemną. Co podstawiając do wzoru na ciepło parowania ΔHp = -R * b daje nam dodatnią liczbę rzeczywistą. Jeżeli ln ze stosunku ciśnień rośnie zauważamy z wykresu że odwrotność temperatury maleje.
Wszystkie pomiary i obliczenia wykonałam dokładnie i starannie, więc uzyskany wynik nie powinien znacząco odbiegać od teoretycznej wartości wykonanych przez mnie pomiarów.
Wyszukiwarka