28.02.2011

ŚREDNI WAŻONY KOSZT KAPITAŁU (WACC)

Numeryczną postacią liczbowym ekwiwalentem w hierarchizacji źródeł pozyskiwania kapitału jest koszt kapitału.

W inwestycjach zawsze jest tak, że każdy pozyskany kapitał z jakiegokolwiek źródła wiąże się z kosztem kapitału. Pod pojęciem koszt kapitału rozumiemy wynagrodzenie dla dawcy tego kapitału.

Jeżeli inwestor, dla realizacji inwestycji zaciąga kredyt to, to co płaci w celu pozyskania tego kredytu czyli suma rat odsetkowych i prowizji jest kosztem kapitału.

Jeżeli inwestor posługuje się emisją akcji, z tego tytułu również ponosi koszty kapitału poprzez to, że musi z akcjonariuszami dzielić się zyskami, płacąc im dywidendy.

Jeżeli inwestycja równocześnie wymaga jednocześnie zasilania wewnętrznego i zewnętrznego, czyli jeżeli inwestycja jest jednocześnie finansowana kapitałami obcymi i własnymi to z różnych źródeł pozyskiwania kapitału mamy różne koszty pozyskiwania kapitału.

Koszt kapitału jest zawsze wyrażony w procencie np. jeżeli koszt kapitału wynosi 10% tzn., że każda złotówka pozyskanego kapitału kosztowała inwestora 10gr.

Jeżeli montaż finansowy pochodzi z różnych źródeł to trzeba policzyć jako średnią, przy czym nie mówi się tu o średniej arytmetycznej (bo waga kapitałów obcych i kapitałów własnych nie jest 0,5 i 0,5), ale o średnim ważonym koszcie kapitału (WACC).

WACC - jedna z centralnych kategorii finansów.

WACC - średnia ważona (gdzie wagami są owe udziały) kosztu kapitału własnego i kosztu kapitału obcego.

gdzie:

KKO - koszt kapitałów obcych (wynagrodzenie dla dawców kapitału obcego - wierzycieli)

KKW - koszt kapitału własnego (wynagrodzenie dla dawców kapitału własnego -

udziałowców)

a₁ - (waga) udział kapitałów obcych w finansowaniu inwestycji

a₂ - (waga) udział kapitałów własnych w finansowaniu inwestycji

Założenie: a₂ = 1 - a₁ - tzn. wagi uzupełniają się co do jedności (np. 0,25 - kapitały własne,

to 0,75 - kapitały obce)

gdzie:

KO - wielkość kapitałów obcych (tzn. ile ich potrzebuję)

KW - wielkość kapitałów własnych

K_c - kapitał całkowity (suma kapitałów własnych i obcych)

Przykład:

K_c = 1000000

KW = 250000 (po koszcie 20%) 0,25 KW

KO = 750000 (po koszcie 10%) 0,75 KO

Ile średnio muszę zapłacić dawcy kapitału bez względu na to skąd ten kapitał pochodzi?

Czyli, każda złotówka pozyskanych kapitałów kosztuje inwestora 12,5 grosza.

Jest to istotne kryterium wartościujące inwestycji.

Oznacza to, że jeżeli kapitały nie są darmowe (a ewidentnie nie są) to inwestycja jest efektywna nie wtedy kiedy ja zarabiam cokolwiek, tylko wtedy, gdy zarabiam więcej niż koszt kapitału.

Jeżeli uzyskiwałbym poziom dochodowości, który nie wystarcza na zaspokojenie żądań dawców kapitału, to mimo że efekty przewyższają nakłady to, to i tak nie ma sensu.

W związku z tym koszt kapitału wyznacza dolny próg rentowności inwestycji.

Ponieważ koszt kapitału jest wyrażony w procencie, to musze znaleźć taką miarę dochodowości inwestycji, która też jest wyrażona w procencie i wtedy te wielkości można we sobą porównać.

Absolutnie centralną kategorią inwestycji wyrażoną w procencie jest stopa zwrotu z inwestycji.

Stopa zwrotu z inwestycji - względną miara efektywności inwestycji i wyraża rentowność

każdej zaangażowanej złotówki nakładów inwestycyjnych.

WACC < E(r)

r - stopa zwrotu

E(r) - oczekiwana stopa zwrotu

Stopa - relacja względem siebie dwóch wielkości (jest zawsze ułamkiem bądź procentem)

a stopa zwrotu r jest stosunkiem sumy dochodów (jakie wygenerowała, albo wygeneruje inwestycja) do sumy nakładów jakie zostały zaangażowane , aby inwestycję zrealizować.

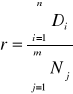
gdzie:

D - dochód
P - przychód

N - nakład

D = P - N

Stopa zwrotu liczona od dochodu jest prostą relacją dochodu przez nakład, a jeżeli stopę zwrotu liczymy od przychodu to relacja przychód przez nakład minus 1.

Przykład:

P = 120

N = 100

D = 120 - 100 = 20

Każda zaangażowana złotówka wygenerowała 20gr dochodu.

Jest to prosta stopa zwrotu i w związku z tym jest często nieprawdziwa.

PODSTAWOWE POSTACI PROSTEJ STOPY ZWROTU

Trzy sztandarowe postaci prostej stopy zwrotu:

- ROE

- ROA

- ROI

ROE - zwrot na kapitale własnym („ile zysku netto wygenerowała złotówka

zaangażowanych kapitałów własnych?”)

gdzie:

Zn - zysk netto

P - przychód

K - koszty

I - odsetki

TAX - podatki

Im wyższe ROE tym lepiej.

ROA - zwrot na aktywach („ile zysku netto wygenerowała jednostka zaangażowanych

aktywów?”); rentowność kapitału całkowitego

gdzie:

A - suma aktywów

Ponieważ w bilansie suma aktywów jest równa sumie pasywów, czyli sumie kapitałów własnych i obcych, a suma kapitałów własnych i obcych to są kapitały całkowite to w tym sensie ROA jest równocześnie rentownością kapitału całkowitego.

Różnicą między ROE, a ROA polega na tym, że:

- ROE pokazuje jaka jest rentowność kapitałów własnych - jak efektywnie pracują kapitały

udziałowców

- ROA odpowiada na pytanie jak efektywnie pracują wszelkie kapitały zaangażowane u

inwestora, zarówno obce jak i własne.

W ROA tkwi przymus finansowy, ze rentowność kapitałów obcych i własnych musi być wyższa od kosztu kapitału obcego i kapitału własnego.

ROI - zwrot na nakładach inwestycyjnych

gdzie:

Ni - suma nakładów inwestycyjnych

EBIT - zysk operacyjny (zysk brutto przed spłatą odsetek i przed zapłatą podatków)

Jeżeli wyłożyłem stówę, zarobiłem 20 to prosta stopa zwrotu wynosi 20%, ale dokładając do tego jeszcze jeden warunek:

100zł - cena zakupu akcji

120zł - cena sprzedaży akcji

Zarobiłem 20 złotych, ale między momentem zakupu tych akcji, a momentem sprzedaży tej akcji minęły równo dwa lata. Jaka jest więc roczna stopa zwrotu z tytułu sprzedaży tej akcji? Nie 10%.

20% - prosta stopa zwrotu za tzw. okres przetrzymania.

Jeżeli stopa zwrotu za dwa lata wynosi 20% to roczna stopa zwrotu nie wynosi 10%, jest id tych 10% niższa.

Dowód:

Równanie na wartość pieniądz w czasie:

np.

P = 120

N = 100

Zakładając, że r=10% otrzymamy równanie:

, a nie 120!

Gdy inwestycja trwa dłużej niż rok, dla obliczenia rocznej średniej stopy zwrotu, trzeba oszacować geometryczną stopę zwrotu.

GEOMETRYCZNA STOPA ZWROTU

I postać: (gry r są równe)

gdzie:

r_g - geometryczna stopa zwrotu

n - liczba lat czasu trwania inwestycji

FV - wartość końcowa inwestycji

PV - wartość początkowa inwestycji

Przykład:

FV=120

PV=100

- roczna stopa zwrotu

Gdybym akcję sprzedał za 121zł to miałbym

Dla okresów dłuższych niż jeden rok zastosowanie ma wyłącznie geometryczna stopa zwrotu !!! (jeżeli mamy obliczyć stopę roczną)

Trzeba kategorycznie odróżniać pojęcie stopa za okres przetrzymania od stopy rocznej!

Okres przetrzymania jest kategorią zróżnicowaną, ale zawsze oznacza to samo - jest to przedział czasowy między zakupem np. papieru wartościowego, a momentem jego sprzedaży.

Przykład 2:

OFERTY BANKÓW
Nazwa banku	Okres lokaty	Oprocentowanie - rok 1	Oprocentowanie - rok II
Bank „A”	2 lata	6%	8%
Bank „B”	2 lata	8%	6%

Która oferta jest korzystniejsza?

Obie są takie same!

Dla zróżnicowanego rocznego oprocentowania wyliczenie średniorocznego oprocentowania jest II postacią konieczności użycia tzw. geometrycznej stopy zwrotu.

Dla 2 lat:

, tak więc obojętne jest czy najpierw będzie 8 czy 6, bo mnożenie przecież jest przemienne.

,
, n - okresów

gdzie:

n - liczba okresów

r₁, r₂, …, r_n - poszczególne stopy zwrotu

∏ - operator mnożenia

II postać: (gdy r są różne)

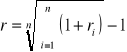
- średnia roczna stopa procentowa dla przykładu 2.

Geometryczna stopa zwrotu ma zastosowanie przy inwestycjach kilkuletnich, przy projektach rzeczowych, a nie prosta stopa zwrotu.

LOGARYTMINCZNA STOPA ZWROTU

Przykład:

PV=100

FV=105

t=1

W jednym przypadku roczna stopa zwrotu wynosi 5% (jeżeli kapitalizacja była jednokrotna i to na koniec okresu), a w nieskończonej ilości przypadków to nie będzie 5%.

Jeżeli stopa jest równa 5% tzn. ze przez cały rok z 100złotymi nie działo się nic, a odsetki zostały dopisane dopiero 31.12.

Gdyby te okresy odsetkowe w skali roku były 2 to:

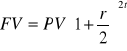
, bo n=2

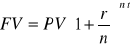
(kurczą się przedziały czasowe)

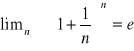
W warunkach kapitalizacji ciągłej:

gdzie:

r - roczna stopa oprocentowania

t - czas trwania inwestycji

Jeżeli kapitalizacja co jeden dzień to

Przykład:

Roczna stopa procentowa 5%, kapitalizacja raz w roku to dostaję 105zł.

Jeżeli półroczna stopa to:

(W Excelu zapisujemy exp(r·t))

Logarytmiczna stopa zwrotu jest stopą zwrotu obliczoną dla warunków kapitalizacji ciągłej.

Wzór na logarytmiczną stopę zwrotu:

r_ln - logarytmiczna stopa zwrotu

więc:

---