Protokół z ćwiczenia nr E1

Temat: Badanie widma promieniowania termicznego na przykładzie widma żarówki z włóknem wolframowym.

Podstawy teoretyczne.

Celem tego ćwiczenia jest wyznaczenie rozkładów widmowych promieniowania termicznego włókna wolframowego żarówki dla kilku temperatur, oraz sprawdzenie prawa przesunięć Wiena.

Samo promieniowanie termiczne jest niczym innym jak emisją promieniowania elektromag- -netycznego, którego źródłem są wykonujące drgania termiczne naładowane elementy układu tj. elektrony, jądra atomowe, jony. Oczywiste jest, że emisja tego promieniowania musi być poprzedzona dostarczeniem energii do układu, która jest niezbędna do wzbudzenia układu do wyższych stanów energetycznych.

Konsekwencją tego rozumowania jest to ,że każde ciało znajdujące się w temperaturze wyższej od temperatury zera bezwzględnego, emituje energię promienistą, której wielkość oraz rozkład zależy od: temperatury bezwzględnej ciała, własności fizykochemicznych i stanu powierzchni danego ciała.

Zawsze jednak część promieniowania padającego na ciało odbija się od niego, a część wchodzi do środka, powodując tym samym podniesienie temperatury ciała. Ta część całkowitej energii padającej w przedziale częstotliwości i , która zostaje przez ciało pochłonięta, nazywa się zdolnością absorbcyjną ciała dla danej częstotliwości. Czyli wskazuje ona, jaka część energii promieniowania padającego jest zaabsorbowana w jednostce czasy przez jednostkę powierzchni.

Jest to liczba niemianowana i oznaczmy ją symbolem a(,T).

Z kolei energia wypromieniowana przez jednostkową powierzchnię ciała w przedziale częstotliwości i w jednostce czasu, nazywa się zdolnością emisyjną oznaczaną symbolem (,T).

Pomiędzy zdolnością absorbcyjną i zdolnością emisyjną ciała zachodzi związek, ujęty przez prawo Kirchhoffa w postaci :

gdzie - E(,T) jest zdolnością ciała doskonale czarnego.

Ciało doskonale czarne - jest to ciało którego zdolność absorbcyjna jest a(,T)=1 dla wszystkich długości fali. Znanych jest kilka modeli ciała doskonale czarnego, jednakże idea wszystkich tych modeli sprowadza się do tego, że otoczona ze wszystkich ścian komora jest połączona z otaczającą przestrzenią, za pośrednictwem małego otworu. Jeśli na otwór pada promieniowanie to ulega ono wielokrotnemu odbiciu od ścian komory i rozproszeniu w jej wnętrzu.

Spośród ciał rzeczywistych bardzo zbliżony do ciała doskonale czarnego rozkład widmowy promieniowania ma wolfram (np. w postaci włókna żarówki). Inne ciała to pozostałe trudno topliwe metale tzn. platyna, tantal, osm, molibden.

Zależność zdolności emisji (czyli ilości energii odpowiadającej wąskiemu przedziałowi długości fali między a + , wysyłanej w jednostce czasu przez jednostkę powierzchni źródła, od długości fali ) promieniowania ciała doskonale czarnego umieszczonego w temperaturze T opisuje poniższy wzór Plancka :

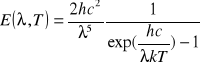
gdzie: h - stała Plancka i wynosi h=

c - prędkość światła c=

k - stała Boltzmanna k=

Zależność tę dla kilku wartości temperatur przedstawia rysunek przedstawia rysunek.

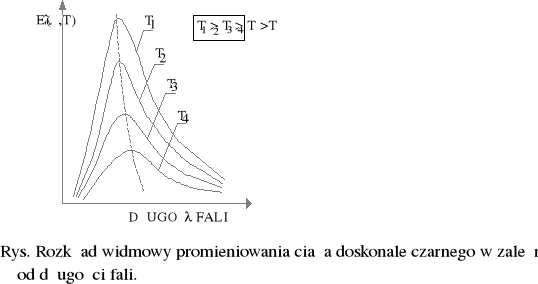
Każda z powyższych krzywych posiada maksimum emisji, które spełniają prawo przesunięć Wiena, mówiące, że długość fali odpowiadająca maksimum zdolności emisji promieniowania ciała doskonale czarnego jest odwrotnie proporcjonalna do temperatury bezwzględnej ciała.

Wzór potwierdzający prawo przesunięć Wiena otrzymuje się po przekształceniu wzoru Plancka i który ma postać:

Wzór Wiena ten umożliwia wyznaczenie temperatury ciała doskonale czarnego, znając położenie maksimum jego widma.

Istnieje jeszcze prawo Stefana-Boltzmanna które mówi, że całkowita energia promieniowania wysyłana przez jednostkę powierzchni ciała doskonale czarnego w jednostce czasu wynosi:

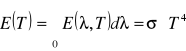
gdzie:
i oznacza stałą Stefana-Boltzmanna.

Wykonanie ćwiczenia.

1. Łączymy obwód wg. schematu, a następnie równoważymy mostek rezystancyjny w którym włączony jest fotorezystor PbS, nastawiając uprzednio zerowe położenie wskazówki w miliwoltomierzu.

2. Włączamy spektrometr Hilgera i nastawiamy prąd żarzenia żarówki.

3. dokonujemy serii pomiarów, nastawiając kolejno długości fali (w przedziale od 650 do 3000 nm) i odczytując wartości napięcia wskazywanego przez miliwoltomierz, które są proporcjonalne do zdolności emisyjnej (,T). Wartości zapisujemy w tabeli pomiarów w protokóle.

4. Z wykresu określającego czułość fotorezystora PbS w funkcji długości fali odczytujemy jego czułość dla każdej wartości długości fali dla której wykonywaliśmy pomiary.

5. Sporządzamy wykres zależności (,T)r od długości fali dla 2 wartości temperatur:

1800K (Pżarówki=14,4W) oraz 1520K (Pżarówki=8,5W).

6. Obliczamy wartość iloczynu maxT

- dla T=1800K

- dla T=1520K

Wnioski.

Nasze wyniki pomiarów są obciążone znacznymi błędami systematycznymi, które w zasadzie są niemożliwe do wyznaczenia. Wynikają one z niedokładności użytych mierników, kiepskich parametrów rezystorów tworzących mostek rezystancyjny w którym pracuje fotorezystor PbS.

Powodowało to ciągłe "derównoważenie" się mostka mimo wcześniejszego zrównoważenia.

Naszym zdaniem wynikało to z tego, że rezystory pod wpływem temperatury (wywołanej przepływem prądu) zmieniały swoją nominalną rezystancję powodując tym samy zmianę parametrów mostka. Można by tego uniknąć używając mostka z kompensacją temperaturową, zrealizowaną np. za pomocą termoelementu odpowiednio włączonego w gałęzie mostka, co pozwoliłoby uniknąć ciągłego "derównoważenia" mostka.

Kolejnymi źródłami niedokładności może być niestabilność źródła zasilania mostka, jak również nieliniowość charakterystyki potencjometru poprzez który zasilany jest mostek.

Nieliniowość ta wynika z wielu zjawisk tzn. niestałości rezystywności drutu i wymiarów karkasu potencjometru na całej jego długości, zmiennej rezystancji przejścia drut-styk ślizgowy i skokowym przebiegiem charakterystyki(zwoje). Źródła tej niedokładności można w prosty sposób zminimalizować stosując dokładny potencjometr gdzie błędy spowodowane nieliniowością nie przekraczają 1%.

Laboratorium z Fizyki.

Strona nr 1

---