Politechnika Częstochowska
Laboratorium Fizyki
Ćwiczenie nr 10.
Temat: Wyznaczanie współczynnika przewodnictwa temperaturowego
ciał stałych.
Dariusz Frydrych Paweł Łakomy
Wydz. Elektryczny
grupa II. 1. Zagadnienia teoretyczne.
Ciała stałe posiadające różne temperatury w różnych punktach, odizolowane od wpływów otoczenia, dążą do wyrównania tych temperatur zgodnie z drugą zasadą termodynamiki. Szybkość wyrównywania się temperatur zależy od ich różnicy i rodzaju ciał. Każde ciało charakteryzuje tzw. współczynnik przewodnictwa temperaturowego zwany też współczynnikiem dyfuzji cieplnej. Wyrównywanie się temperatur spowodowane jest przepływem ciepła z obszarów o wyższej temperaturze do obszarów o temperaturze niższej. Zdolność przewodzenia ciepła przez ciało charakteryzuje współczynnik przewodnictwa cieplnego ℜ. Oba powyższe współczynniki powiązane są zależnością:
K=
gdzie: ζ - gęstość ciała
c - ciepło właściwe ciała.
Przepływ ciepła w ciele można opisać równaniem:
We wzorze występuje gradient temperatury, co wskazuje, że proces przenoszenia energii cieplnej podlega prawom statystyki. Proces przenoszenia zachodzi w ten sposób, że energia z jednego końca próbki nie przenosi się do drugiego po linii prostej, lecz nośniki energii dyfundują przez próbkę ulegając licznym zderzeniom.
W mechanice kwantowej ruch cząsteczek wiąże się z rozchodzeniem się fal. Współczesna teoria przewodnictwa cieplnego wiążę się z istnieniem cząsteczek zw. fononami. W temperaturze zera bezwzględnego fonony nie istnieją, a wraz ze wzrostem temperatury rośnie ich ilość. Przewodnictwo cieplne gazów można opisać wzorem:
*)
Dla gazu fotonowego c - będzie ciepłem właściwym substancji, l - średnią drogą fononów między kolejnymi zderzeniami, u - prędkością dźwięku (fononów). Przewodnictwo cieplne w dielektrykach jest ograniczone ze względu na „odbijanie” części fononów. Średnia droga swobodna fononów będzie zależała od ich ilości, czyli także od temperatury. W bardzo niskich temperaturach przewodnictwo cieplne zależy tylko od ciepła właściwego gdyż droga swobodna fononów osiąga rozmiary kryształów.
Metale zasadniczo różnią się od dielektryków. Tutaj oprócz fononów ciepło przenosi także gaz elektronowy. Elektrony są tak dobrym przewodnikiem ciepła, że przewodnictwo cieplne metali jest nawet 100 razy większe, niż w dielektrykach. W metalach w wysokich temperaturach ciepło przewodzą wyłącznie elektrony i przewodnictwo cieplne jest w zasadzie stałe.
Półprzewodniki o bardzo małej koncentracji elektronów w paśmie przewodnictwa mają przewodnictwo cieplne zbliżone do dielektryków, natomiast gdy koncentracja elektronów w paśmie przewodnictwa jest duża, przewodnictwo cieplne jest zbliżone do metali.
Całkiem odmiennie zmienia się z temperaturą przewodnictwo cieplne w ciałach polikrystalicznych, w których krystality są małe w porównaniu ze średnią drogą swobodną fononów, a także w ciałach amorficznych, które można traktować jak ciała polikrystaliczne z kryształami o rozmiarach atomów. W ciałach takich przewodnictwo cieplne w bardzo niskich temperaturach powinno rosnąć z temperaturą tak, jak ciepło właściwe, a następnie, ponieważ ani c, ani l nie zależą od temperatury, przewodnictwo cieplne pozostaje stałe.
Prawdziwe jest równanie:
Wykres tej funkcji poczynając od pewnej chwili t jest prostą o współczynniku kątowym -Kλ1. Mierząc temperaturę w dowolnym punkcie wewnątrz ciała w funkcji czasu i znając , zależną od kształtu próbki, możemy znaleźć współczynnik przewodnictwa temperaturowego K.
Jeżeli zlutujemy końcami dwa przewody z różnych materiałów i jedno ze spojeń podgrzejemy utrzymując drugie w niskiej temperaturze, to w powstałym obwodzie popłynie prąd elektryczny. Zjawisko to wykorzystano do budowy termopar czyli ogniw termoelektrycznych. Jeśli znamy siły elektromotoryczne wytwarzane w określonej temperaturze, to takie ogniwo może służyć do pomiaru temperatury.
2. Układ pomiarowy.
*) Aparatura do cechowania termopary Cu-konstantan.
AT - autotransformator
KE - kuchenka elektryczna
N - naczynie aluminiowe
C - denko tekstolitowe
T - termometr rtęciowy
E - termopara Cu-konstantan
G - galwanometr zwierciadłowy.
*) Aparatura do wyznaczania współczynnika przewodnictwa temperaturowego.
UT - ultratermostat
P - walcowata próbka z plexiglasu
B - denko bakielitowe
E - termopara Cu-konstantan
G - galwanometr zwierciadłowy.
T - termometr rtęciowy
3. Tabele pomiarowe.
Tabela 1.
Lp. |
Temperatura [°C] |
Temperatura [K] |
STEM [dz] |
STEM [mV] |
1 |
20 |
293 |
0.5 |
0.015 |
2 |
22 |
295 |
1 |
0.03 |
3 |
24 |
297 |
5 |
0.15 |
4 |
26 |
299 |
8 |
0.24 |
5 |
28 |
301 |
11 |
0.33 |
6 |
30 |
303 |
15 |
0.45 |
7 |
32 |
305 |
19 |
0.57 |
8 |
34 |
307 |
21.5 |
0.645 |
9 |
36 |
309 |
24 |
0.72 |
10 |
38 |
311 |
27 |
0.81 |
11 |
40 |
313 |
32 |
0.96 |
12 |
42 |
315 |
36 |
1.08 |
Tabela 2.
Lp. |
STEM [dz] |
STEM [mV] |
ΔT=T0-Tp [K] |
czas [s] |
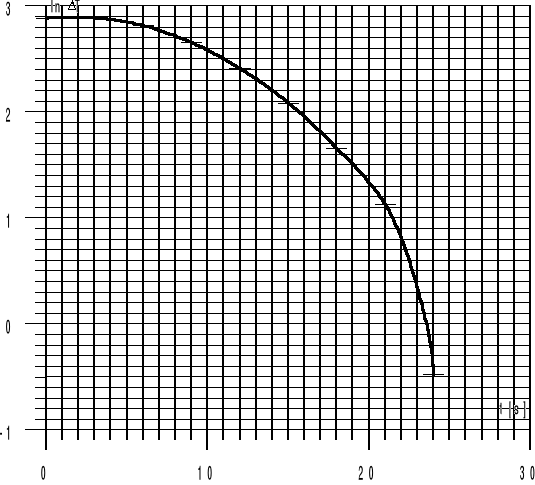
ln ΔT |
1 |
29 |
0.87 |
17.922 |
0 |
2.886 |
2 |
29 |
0.87 |
17.922 |
180 |
2.886 |
3 |
27 |
0.81 |
16.686 |
360 |
2.8145 |
4 |
23 |
0.69 |
14.214 |
540 |
2.6542 |
5 |
18 |
0.54 |
11.124 |
720 |
2.4091 |
6 |
13 |
0.39 |
8.0339 |
900 |
2.0836 |
7 |
8.5 |
0.255 |
5.253 |
1080 |
1.6587 |
8 |
5 |
0.15 |
3.09 |
1260 |
1.1281 |
9 |
1 |
0.03 |
0.618 |
1440 |
-0.4812 |
10 |
-1 |
-0.03 |
-0.618 |
1620 |
|
11 |
-4 |
-0.12 |
-2.472 |
1800 |
|
12 |
-5.5 |
-0.165 |
-3.399 |
1980 |
|
13 |
-3 |
-0.09 |
-1.854 |
2160 |
|
14 |
-9 |
-0.27 |
-5.562 |
2340 |
|
15 |
-10 |
-0.3 |
-6.18 |
2520 |
|
4. Obliczenia :
a) Wyznaczenie stałej pomiaru temperatury termoparą z charakterystyki STEM=f(T).
Przyjmując że charakterystyka jest prostą wynika , że temperatura jest proporcjonalna do STEM. T∼STEM
C = ( Tk-Tp) / (STEMk-STEMp) = (315-293) / (1.08-0.015) = 20.65 [K/mV]
b) Wyznaczenie róznicy temperatur : ΔT = C • STEM
np. ΔT1 = 20.65 • 0.87 = 17.992 [K]
c) Wyznaczenie tgα z prostoliniowej części wykresu lnΔT = f (t) :
tgα = (2.4 - 1) / ((22.2-13)•60) = 2.5326 • 10-3 [1/s]
d) Wyznaczenie współczynnika λ m,n,l
λ m,n,l = (μm(n) / r)2 + (l π / z)2
gdzie : r - promień walca równy 25•10-3 [m]
z - wysokość walca równa 115•10-3 [m]
l = 1 , μm(n) = 2.4
λ = (2.4 / (25•10-3))2 + (l π / 115•10-3)2 = 9216 + 745.5 = 19177.5 [1/m2]
e) Wyznaczenie współczynnika przewodnictwa temperaturowego pleksi :
K= tgα / λ =2.5326•10-3/19177.5 = 1.3225•10-7 [m2/s]
Wnioski :
W przeprowadzonym ćwiczeniu podczas wyznaczania współczynnika przewodnictwa temperaturowego pleksi otrzymane wartości STEM z pomiaru są błędne .Galwanometr najpierw wskazywał wartość dodatnią STEM, która po czasie ok. 24 min. zmalała do zera.
Następnie plamka galwanomatru coraz bardziej zaczęła się wychylać w drugą stronę wsazując przeciwny zwrot STEM , by po czasie ok. 20 min. osiągnąć wartość -10 mV. Z pomiarów tych wynika iż najpierw po zanużeniu pleksi do gorącej cieczy środek walca ma niższą temperaturę od otaczajacej go cieczy co powoduje wytworzenie STEM następnie po ogrzaniu pleksi dochodzi do zrównania temperatur dzięki czemu STEM = 0. Nastepnie zaobserwowaliśmy coś co nie powinno mieć tutaj miejsca - wychylenie plamki galwanometru w drugą stronę , co pozwala twierdzić iż środek walca z pleksi był cieplejszy od otaczajacej go cieczy . Przyczyną zaistniałego zjawiska mogła być niepoprawna praca termostatu , przez co temperatura cieczy stała się niższa od temperatury środka walca z pleksi pnieważ ciecz szybciej stygnęła niż środek walca . Dalsze obliczenia przeprowadziliśmy dla wartości dodatnich STEM , gdyż wartości ujemne nie powinny wogóle tutaj wystąpić , a poza tym nie istnieje ln z wartości ujemnej .Wyznaczona wartość tgα jest obarczona bardzo dużym błędem , gdyż otrzymana charakterystyka lnΔT = f(t) jest bardzo szybko opadająca i nie można precyzynie określić odcinka najbardzij priostoliniowego odcinka w którym należy obliczyć tg kąta nachylenia jej do osi czasu .
Charakterystyka STEM = f(T)
Charakterystyka lnΔT = f (t)
Wyszukiwarka