Politechnika Łódzka Katedra Mikroelektroniki i Technik Informatycznych 90-924 Łódź, Wólczańska 221/223 Tel: [phone] Fax: + 48 42 636 03 27 http://www.dmcs.p.lodz.pl

Laboratorium

Metody Numeryczne (magisterskie)

wersja kwiecień 2013

Przepisy laboratorium:

1. Ocena z laboratorium wystawiana jest na podstawie raportów i wyników z ćwiczeń.

2. Laboratorium jest obowiązkowe i każda nieuzasadniona nieobecność nie jest dozwolona.

3. Studenci, którzy nie są przygotowani do laboratorium, mogą nie zostać dopuszczeni do wykonania ćwiczenia.

4. Zapisywanie plików i praca poza katalogami domowymi są zabronione.

5. Studenci wykonujący każde z nieprzyzwoitych czynności (np. łamanie haseł, używania złośliwego oprogramowania, itp.) będą natychmiastowo usuwani z zajęć.

6. Niedozwolone jest używanie własnych komputerów i oprogramowania.

Spis treści

Ćwiczenie 1 (tygodnie 1-2)
Całkowanie numeryczne

Zadanie 1.1 Kwadratury Newtona-Cotesa

Napisz w Matlabie procedurę pozwalającą na obliczanie dla danego przedziału całkowania i zmiennej liczby punktów całek oznaczonych używając metod prostokątów, trapezów i Simpsona. W wyniku obliczeń procedura powinna zwrócić wartość całki oznaczonej. Wykorzystując napisaną procedurę przeprowadź analizę błędu całkowania w zależności od liczby podprzedziałów całkowania dla funkcji określonych w tabeli.

Tabela 1: Funkcje podcałkowe i przedziały całkowania.

Funkcja	Przedział
5x^3 + x - 3	[1, 2]
cos(x)	[0, 1]
ln(x)	[1, 2]

Zadanie 1.2 Metoda Romberga

Korzystając z wyników poprzednich obliczeń wykorzystaj metodę Romberga do obliczenia całek powyższych funkcji. Porównaj dokładność metod.

Zadanie 1.3 Kwadratury Gaussa-Legendre'a

Powtórz podobne analizy wykorzystując kwadratury Gaussa-Legendre'a różnego rzędu. Wykorzystaj wartości współczynników podanych w tabeli. Pamiętaj o mapowaniu przedziałów całkowania na przedział [-1, 1].

Tabela 2: Współczynniki kwadratur Gaussa-Legendre'a.

Rząd	Węzły	Wagi
n	xk	wk
1	0.0	2.0
2	± 0.5773502692	1.0
3	± 0.7745966692 0.0	0.5555555556 0.8888888889
4	± 0.8611363116 ± 0.3399810436	0.3478548451 0.6521451549
5	± 0.9061798459 ± 0.5384693101 0.0	0.2369268851 0.4786286705 0.5688888889
6	± 0.9324695142 ± 0.6612093865 ± 0.2386191861	0.1713244924 0.3607615730 0.4679139346
7	± 0.9491079123 ± 0.7415311856 ± 0.4058451514 0.0	0.1294849662 0.2797053915 0.3818300505 0.4179591837
8	± 0,9602898565 ± 0,7966664774 ± 0,5255324099 ± 0,1834336425	0,1012285363 0,2223810345 0,3137066459 0,3626837834

Ćwiczenie 2 (tygodnie 3-4)
Zagadnienia początkowe dla równań różniczkowych zwyczajnych

Zadanie 2.1 Metody jednokrokowe

Napisz w Matlabie procedury umożliwiające rozwiązywanie ze zmiennym krokiem zagadnień początkowych dla równań różniczkowych zwyczajnych używając metod jednokrokowych umieszczonych w tabeli poniżej. Wykorzystaj te metody do znalezienia wartości y (1) dla następującego zagadnienia:

.

Dla każdej z metod porównaj otrzymane wyniki dla różnych wartości kroku z rozwiązaniem dokładnym. Ponadto dla wszystkich rozważanych metod wykreśl błąd w funkcji liczby kroków.

Tabela 1: Wykaz metod jednokrokowych

Metoda	Równanie
Eulera
Heuna
Rungego-Kutty 4. rzędu

Zadanie 2.2 Metody wielokrokowe

Wykonaj te same analizy dla powyższego zagadnienia z wykorzystaniem wielokrokowych metod drugiego rzędu wymienionych w tabeli poniżej. Dla rozwiązania zagadnienia należy przekształcić funkcję podaną w tabeli
do postaci jawnej. Jeśli będzie to konieczne wykonaj początkowe kroki używając metody Rungego-Kutty 4. rzędu.

Tabela 2: Wykaz metod wielokrokowych.

Metoda	Równanie
Adamsa-Bashfortha 2. rzędu
Adamsa-Moultona 2. rzędu
Geara 2. rzędu

Ćwiczenie 3 (tygodnie 5-7)
Metoda różnic skończonych

Zadanie 3.1 Jednowymiarowa analiza temperaturowa w stanie ustalonym

Rozważmy proces nagrzewania cienkiej płyty materiału o grubości a = 1 cm. Płyta ta jest nagrzewana
na powierzchni x = 0 strumieniem ciepła q o wartości 20 000 W/m² i chłodzona na powierzchni x = a zgodnie
z prawem Newtona ze współczynnikiem wymiany ciepła h = 1 000 W/m²K. Ponadto we wnętrzu płyty zachodzi równomierna generacja ciepła o gęstości objętościowej mocy g = 4 MW/m³. Temperatura otoczenia równa jest temperaturze początkowej płyty i wynosi 0 °C. Przewodność cieplna materiału wynosi  = 10 W/mK. W stanie równowagi rozkład temperatury w płycie jest opisany równaniem Poissona:

a rozwiązanie analityczne dane jest wzorem:

.

Znajdź numeryczne rozwiązanie powyższego problemu dla stanu ustalonego stosując do rozwiązania metodę różnic skończonych i porównaj je z rozwiązaniem dokładnym. Zbadaj wpływ rozmiaru siatki na uzyskiwane rozwiązania.

Zadanie 3.2 Jednowymiarowa czasowa analiza temperaturowa

Dla wystarczająco gęstej siatki przeprowadź analizę czasową powyższego problem za pomocą metody różnic skończonych. Załóż, że dyfuzyjność termiczna materiału  wynosi 5 * 10^-5 m²/s. Rozkład temperatury w płycie jest opisany następującym parabolicznym cząstkowym różniczkowym równaniem ciepła:

a rozwiązanie analityczne wyraża się następującym wzorem:

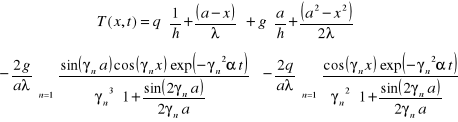
gdzie γ_n są kolejnymi pierwiastkami równania:

.

Porównaj rozwiązania otrzymane numerycznie z dokładnym rozwiązaniem analitycznym. Zbadaj wpływ kroku czasowego na zbieżność schematów Eulera i Cranka-Nicholsona. Kiedy analiza stanie się niestabilna? Czy zmiana parametrów materiałowych ma wpływ na stabilność metody numerycznej?

1

3

---