Wydział Elektroniki Politechniki Wrocławskiej	Laboratorium fizyki ogólnej
^Wykonał Pirosz Paweł		^Grupa 5	^Ćw. nr 8	^Prowadzący dr Anna Wróbel
Wyznaczanie współczynnika lepkości cieczy na podstawie prawa Stokesa		^Data wykonania 98.03.30	^Data oddania 98.04.07	^Ocena

CEL ĆWICZENIA:

Badanie ruchu ciał spadających w ośrodku ciekłym, wyznaczenie współczynnika lepkości cieczy metodą Stokesa, wyznaczenie współczynnika lepkości cieczy za pomocą wiskozymetru Höpplera.

WSTĘP:

Lepkością lub tarciem wewnętrznym nazywamy zjawisko występowania sił stycznych przeciwstawiających się przemieszczeniu jednych części ciała względem innych jego części. Zjawisko to powstaje na skutek ruchów cieplnych cząstek oraz sił międzycząsteczkowych. Wskutek działania siły tarcia wewnętrznego występującego między warstwami cieczy, poruszająca się warstwa pociąga za sobą warstwy sąsiadujące z nią z prędkością tym bardziej zbliżoną do prędkości własnej, im ciecz jest bardziej lepka. Analogicznie - spoczywająca warstwa hamuje poruszające się warstwy sąsiednie. Ze względu na to, że wszystkie rzeczywiste ciecze są lepkie zjawisko lepkości odgrywa istotną rolę podczas przepływu cieczy oraz podczas ruchu ciała stałego w ośrodku ciekłym.

Prawo empiryczne określające siłę oddziaływania występującą między dwiema warstwami cieczy podał Newton. Można je wyrazić wzorem:

Siła F_t, jaką wywierają na siebie nawzajem dwie sąsiadujące ze sobą warstwy płynu, jest proporcjonalna do iloczynu ich powierzchni styku S i gradientu prędkości dv/dx. Współczynnik proporcjonalności η [N⋅s⋅m^-2] nazywamy współczynnikiem lepkości. Współczynnik lepkości ośrodka zależy od temperatury T. Dla cieczy słuszna jest w przybliżeniu zależność:

gdzie C, b są stałymi charakteryzującymi ciecz.

Zjawisko lepkości, podobnie jak dyfuzja i przewodnictwo cieplne, należy do grupy zjawisk obejmowanych wspólną nazwą zjawisk transportu. W zjawiskach lepkości, dzięki ruchom cieplnym cząstek cieczy, mamy do czynienia z transportem pędu między warstwami poruszającymi się z różną prędkością. Ten właśnie transport sprzyja wyrównaniu się prędkości w całym strumieniu przepływającej cieczy.

Ciało stałe, poruszające się w ośrodku ciekłym, napotyka na opór. W otoczeniu ciała obserwujemy wtedy ruch cieczy. Mechanizm tego zjawiska jest następujący: warstwa cieczy, przylegająca do powierzchni poruszającego się ciała, wprawia w ruch pozostałe warstwy cieczy. Tak więc istotną rolę odgrywa tu lepkość cieczy. Dla ciał o symetrii osiowej poruszającego się w kierunku osi, wypadkowa siła oporu działa przeciwstawnie do kierunku ruchu. Doświadczalnie stwierdzono, że dla małych prędkości siła tarcia wewnętrznego F_t jest wprost proporcjonalna do prędkości v, zależy od charakterystycznego wymiaru liniowego ciała l oraz od współczynnika lepkości cieczy .

Równanie określające siłę oporu (tarcia wewnętrznego) ma postać:

F_t = -alv

gdzie a jest to stała zależna od kształtu ciała. Dla kuli o promieniu r (l = r) mamy a=6 i równanie przechodzi w tzw. prawo Stokesa:

F_t = -6rv

Rozpatrzmy ruch małej kulki o promieniu r, spadającej swobodnie w cieczy lepkiej. Na kulkę działają siły:

- ciężar kulki P=mg=ρVg,

- siła wyporu Archimedesa W=-ρ'Vg,

- siła oporu wynikająca z ruchu F_t = -6rv

przy czym: V=4/3r³ - objętość kulki, ρ - gęstość materiału kulki, ρ' - gęstość cieczy.

Siła wypadkowa F, działająca na ciało wynosi

F=P+W+F_t

i jest ona siłą malejącą. Przyczyną takiego stanu jest zwiększanie się prędkości kulki i w konsekwencji wzrost wartości siły F_t. Przyspieszenie ciała maleje zatem w czasie, a prędkość dąży do wartości granicznej, odpowiadającej stanowi F=0.

Równanie ruchu kulki ma postać:

Rozwiązaniem tego równania różniczkowego (przy założeniu, że t₀=0, v(t₀)=0) jest funkcja

gdzie
,
.

Prędkość graniczną (prędkość stała)

ściśle zatem kulka osiąga po czasie nieskończenie długim. W rzeczywistości jednak już po niedługim czasie ruch można z dobrym przybliżeniem uważać za jednostajny. Podstawiając do tego wzoru A i B, otrzymujemy

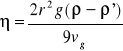
Zauważmy, że wzór ten jest ściśle słuszny tylko dla obszaru nieograniczonego cieczy. Jeżeli badana ciecz znajduje się w naczyniu, to należy uwzględnić działania ścianek na ruch kulki. Możemy zatem w przypadku kulki spadającej w cieczy przedstawić współczynnik lepkości w postaci

η=k(ρ-ρ`)t

Stałą k określają warunki doświadczenia, a t jest czasem przebycia zadanej drogi w ruchu jednostajnym.

WYKAZ PRZYRZĄDÓW :

• naczynie z badaną cieczą

• aerometr

• zestaw kulek

• waga analityczna

• śruba mikrometryczna

• linijka z podziałką milimetrową

• stoper

• wiskozymetr Höpplera

PRZEBIEG ĆWICZENIA :

1. Pomiar współczynnika lepkości cieczy metodą Stokesa w szerokim naczyniu cylindrycznym

Wyznaczenie współczynnika lepkości metodą Stokesa , posługując się szerokim szklanym naczyniem cylindrycznym wypełnionym badaną cieczą . Na zewnętrznej powierzchni bocznej naczynia znajdują się dwa przesuwne pierścienie. Za ich pomocą ustalamy drogę pomiarową odpowiadającą ruchowi jednostajnemu kulki w cieczy. Areometrem wyznaczamy gęstość cieczy. Śrubą mikrometryczną mierzymy średnicę kulki. Wybraną kulkę puszczamy swobodnie tuż nad powierzchnią cieczy w ten sposób, aby jej tor w przybliżeniu pokrywał się z osią naczynia. Czas opadania kulki na drodze między dwoma pierścieniami mierzymy stoperem.

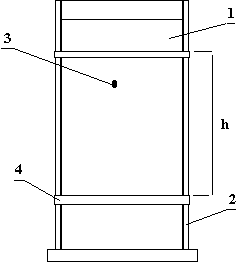
Urządzenie do pomiaru współczynnika lepkości cieczy metodą Stokesa:

1 - ciecz

2 - cylinder szklany

3 - spadająca kulka

4 - pierścienie

h - odległość między pierścieniami.

a) pomiar masy kulek

Tabela 1. Wyniki pomiaru masy kulek
Kulka	m	m
		[ g ]	[ g ]
Kulka 1	0,4342	0,0001
Kulka 2	4,4638	0,0001
Kulka 2	1,3416	0,0001

b) pomiar średnic kulek

Tabela 2. Wyniki i błędy pomiaru średnicy kulek
Lp.	Kulka 1			Kulka 2			Kulka 3
		d	d	δd	d	d	δd	d	d	δd
		[ mm ]	[ mm ]	[ % ]	[ mm ]	[ mm ]	[ % ]	[ mm ]	[ mm ]	[ % ]
1	4,76	0,01	0,21	15,10	0,03	0,20	11,55	-0,25	-2,12
2	4,75	0,00	0,00	15,14	0,07	0,46	11,72	-0,08	-0,68
3	4,76	0,01	0,21	15,08	0,01	0,07	11,39	-0,41	-3,47
4	4,73	-0,02	-0,42	14,93	-0,14	-0,93	12,08	0,28	2,37
5	4,75	0,00	0,00	14,93	-0,14	-0,93	11,77	-0,03	-0,25
6	4,76	0,01	0,21	15,07	0,00	0,00	12,12	0,32	2,71
7	4,75	0,00	0,00	15,13	0,06	0,40	11,77	-0,03	-0,25
8	4,76	0,01	0,21	15,03	-0,04	-0,27	12,11	0,31	2,63
9	4,73	-0,02	-0,42	15,12	0,05	0,33	12,12	0,32	2,71
10	4,76	0,01	0,21	15,13	0,06	0,40	11,40	-0,40	-3,39
	dśr	σ		dśr	σ		dśr	σ	
	4,75	0,01		15,07	0,03		11,80	0,10	

Wartość średnia:

Błąd bezwzględny: d = d_i - d_śr gdzie d_i jest wartością średnicy w kolejnym pomiarze (i=1,2,...,10)

Błąd względny:

Odchylenie standardowe: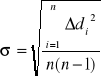
d_śr  σ

Np. d_śr = 1/10⋅(4,76+4,75+…+4,76) = 4,75 [mm]

d = 4,76-4,75 = 0,01 [mm]

δd = 0,01/4,75⋅100 = 0,21 [%]

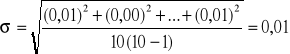
[mm]

c) pomiar odległości między pierścieniami

h = (25,5 ± 0,1) cm

d) wyznaczenie gęstości cieczy

ρ_c=1,24 [g/ml]

e) pomiar czasu opadania kulki w cieczy na drodze między pierścieniami

Tabela 3. Wyniki i błędy pomiaru czasu opadania kulek
Lp.	Kulka 1			Kulka 2			Kulka 3
		T	t	δt	t	t	δt	t	t	δt
		[ s ]	[ s ]	[ % ]	[ s ]	[ s ]	[ % ]	[ s ]	[ s ]	[ % ]
1	1,44	-0,03	-2,04	1,16	-0,02	-1,69	5,51	0,30	5,76
2	1,47	0,00	0,00	1,14	-0,04	-3,39	5,51	0,30	5,76
3	1,45	-0,02	-1,36	1,16	-0,02	-1,69	5,49	0,28	5,37
4	1,41	-0,06	-4,08	1,13	-0,05	-4,24	4,48	-0,73	-14,01
5	1,49	0,02	1,36	1,14	-0,04	-3,39	5,51	0,30	5,76
6	1,50	0,03	2,04	1,25	0,07	5,93	5,47	0,26	4,99
7	1,52	0,05	3,40	1,22	0,04	3,39	4,48	-0,73	-14,01
8	1,48	0,01	0,68	1,23	0,05	4,24	4,55	-0,66	-12,67
9	1,42	-0,05	-3,40	1,16	-0,02	-1,69	5,54	0,33	6,33
10	1,49	0,02	1,36	1,19	0,01	0,85	5,57	0,36	6,91
	tśr	σ		tśr	σ		tśr	σ	
	1,47	0,01		1,18	0,01		5,21	0,15	

Wartość średnia:

Błąd bezwzględny: t = t_i - t_śr gdzie t_i jest wartością czasu w kolejnym pomiarze (i=1,2,...,10)

Błąd względny:

Odchylenie standardowe: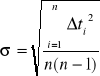
t_śr  σ

Np. t_śr = 1/10⋅(1,44+1,47+…+1,49) = 1,47 [s]

d = 1,44-1,47 =- 0,03 [s]

δd = -0,03/1,47⋅100 = -2,04 [%]

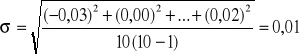
[s]

f) wyznaczenie gęstości kulki

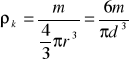
gdzie:
- promień kulki, m - masa kulki

Tabela 4. Wyniki obliczeń gęstości kulek
Kulka	ρk	ρk	δρk
		[ g/ml ]	[ g/ml ]	[ % ]
Kulka 1	7,74	0,05	0,65
Kulka 2	2,49	0,02	0,80
Kulka 2	1,56	0,04	2,56

1ml = 1000mm³ = 1cm³

Błąd ρ_k wyznaczymy z różniczki zupełnej:

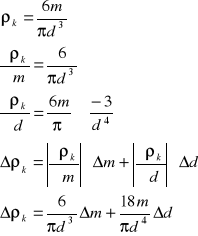
Obliczenia:

g) wyznaczenie współczynnika lepkości

gdzie:

g = 9,81 [m/s²] - przyspieszenie ziemskie, t - czas opadania kulki, ρ_k - gęstość kilki, ρ_c - gęstość cieczy, d - średnica kulki

Tabela 5. Wyniki obliczeń i błąd wyznaczenia współczynnika lepkości
Kulka 1			Kulka 2			Kulka 3
		δ			δ			δ
[ Nsm^2 ]	[ Nsm^2]	[ % ]	[ Nsm^2]	[ Nsm^2]	[ % ]	[ Nsm^2]	[ Nsm^2]	[ % ]
0,461	0,006	1,302	0,607	0,010	1,648	0,496	0,023	4,637

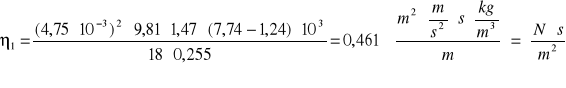
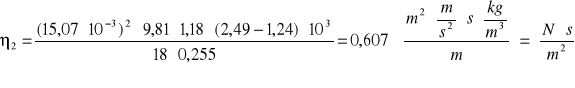
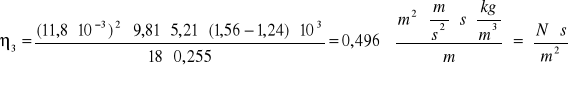
Błąd wyznaczenia współczynnika lepkości wyznaczymy z różniczki zupełnej:

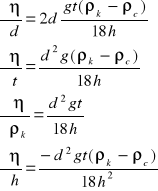
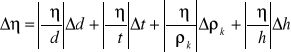
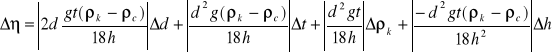
Obliczenia:

_=2⋅4,75⋅10^-3⋅9,81⋅1,47⋅(7,74-1,24)⋅10³⋅0,01⋅10^-3/(18⋅0,255)+(4,75⋅10^-3)²⋅9,81⋅(7,74-1,24)⋅10³⋅0,01/(18⋅0,255)+ +(4,75⋅10^-3)²⋅9,81⋅1,47⋅0,05/(18⋅0,255)+(4,75⋅10^-3)²⋅9,81⋅1,47⋅(7,74-1,24)⋅10³⋅0,1⋅10^-2/(18⋅0,255)=0,006 [Nsm^-2]

_=2⋅15,07⋅9,81⋅1,18⋅(2,49-1,24)⋅0,03⋅10^-3/(18⋅0,255)+(15,07⋅10^-3)²⋅9,81⋅(2,49-1,24)⋅10³⋅0,01/(18⋅0,255)+ +(15,07⋅10^-3)²⋅9,81⋅1,18⋅0,02/(18⋅0,255)+(15,07⋅10^-3)²⋅9,81⋅1,18⋅(2,49-1,24)⋅10³⋅10^-3/(18⋅0,255)=0,010 [Nsm^-2]

_=2⋅11,8⋅10^-3⋅9,81⋅5,21⋅(1,56-1,24)⋅10³⋅0,1⋅10^-3/(18⋅0,255)+(11,8⋅10^-3)²⋅9,81⋅(1,56-1,24)⋅10³⋅0,15/(18⋅0,255)+ +(11,8⋅10^-3)²⋅9,81⋅5,21⋅0,04/(18⋅0,255)+(11,8⋅10^-3)²⋅9,81⋅5,21⋅(1,56-1,24)⋅10³⋅0,1⋅10^-2/(18⋅0,255)=0,023 [Nsm^-2]

δ₁ = 0,006/0,461⋅100% = 1,302 [%]

δ₂ = 0,010/0,607⋅100% = 1,648 [%]

δ₃ = 0,023/0,496⋅100% = 4,637 [%]

Współczynnik lepkości cieczy wynosi:

₁= (0,461 ± 0,006)

₂ = (0,607 ± 0,010)

₃ = (0,496 ± 0,023)

2. Pomiar współczynnika lepkości cieczy metodą Stokesa za pomocą wiskozymetru Höpplera

Inną metodą jest pomiar współczynnika lepkości metodą Stokesa z wykorzystaniem wiskozymetru Höpplera. Stosunkowo duża kulka porusza się cieczy zamkniętej w szklanej rurce. Całość znajduje się w osłonie termostatycznej. Rurka może się obracać wokół osi a - a', prostopadłej do ramienia statywu o kąt 180°. Droga pomiarowa jest określona przez kreski znaczące w rurce. Stała k przyrządu jest zatem ściśle określona. Gęstość cieczy jest podana. Mierząc czas ruchu kulki na odcinku między kreskami, wyznaczamy współczynnik lepkości cieczy w oparciu o wzór  k(ρ_kρct.

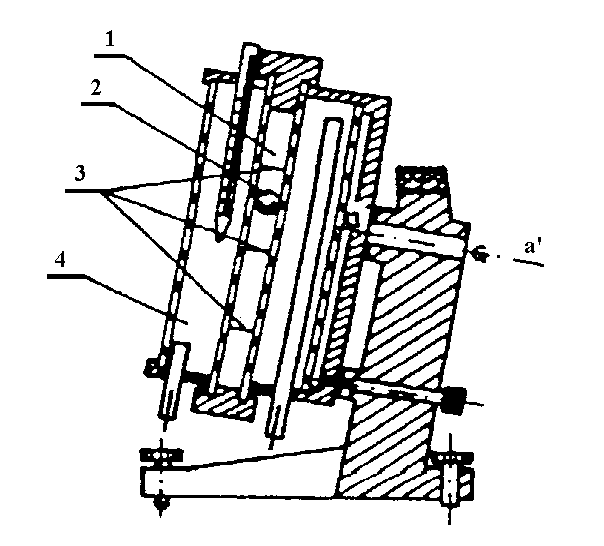
Wiskozymetr Höpplera:

1 - rurka

2 - kulka

3 - kreski, między którymi mierzy się czas spadania kulki

4 - osłona termostatyczna

Warunki pomiaru:

k = 0,7941⋅10-3 [Nsm^-2cm³g^-1s^-1]

ρ_k = (2,41 ± 0,01) [gcm^-3]

ρ_c = (1,235 ± 0,005) [gcm^-3]

Pomiar czasu opadania kulki:

Tabela 6. Wyniki pomiaru czasu
Lp.	T	t	δt
		[ s ]	[ s ]	[ % ]
1	159,74	2,99	1,87
2	158,33	1,58	1,00
3	157,16	0,41	0,26
4	156,67	-0,08	-0,05
5	155,66	-1,09	-0,70
6	154,93	-1,82	-1,17
7	154,75	-2,00	-1,29
Wartość średnia	tśr	σtśr	-
		156,75	0,43	-

t = t_i - t_śr gdzie t_i jest wartością czasu w kolejnym pomiarze (i=1,2,...,10)

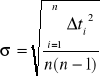
Obliczenia:

 k(ρ_kρ_ct

 = 0,7941⋅10^-3⋅(2,41-1,235)⋅156,75 = 0,146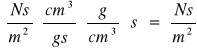

Błąd  wyznaczymy z różniczki zupełnej:

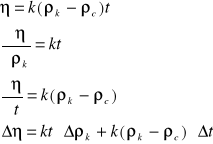
 = 0,7941⋅10^-3⋅156,75⋅0,01 + 0,7941⋅10^-3⋅(2,41-1,235)⋅0,43 = 0,002 [Nsm^-2]

Współczynnik lepkości cieczy wynosi:  = (0,146 ± 0,002)

WNIOSKI I UWAGI:

Z zastosowanych w ćwiczeniu dwóch metod pomiarowych za metodę wnoszącą mniejszy błąd pomiaru należy uważać pomiar wiskozymetrem Höpplera, gdyż błąd pomiaru zależy tylko od błędu pomiaru czasu opadania kulki (jest to błąd wynikający z czasu reakcji obserwatora). Na błąd pomiaru w szerokim naczyniu cylindrycznym składają się takie czynniki jak: błąd pomiaru czasu opadania kulki, błąd pomiaru wysokości odległości między pierścieniami, błąd pomiaru średnicy kulki oraz błąd pomiaru gęstości kulki. W metodzie tej pominięto oddziaływanie ścianek naczynia na ruch kulki. Można je pominąć dla bardzo szerokiego i wysokiego naczynia lub bardzo małych kulek. Otrzymane współczynniki lepkości były różne w zależności od wykorzystywanej kulki. Wynika to z faktu, że różne materiały mają różne współczynniki tarcia z cieczą, które to współczynniki zależą od stopnia gładkości powierzchni oraz rodzaju użytego materiału. Z pomiaru gęstości cieczy areometrem wynika, że badaną cieczą może być gliceryna.

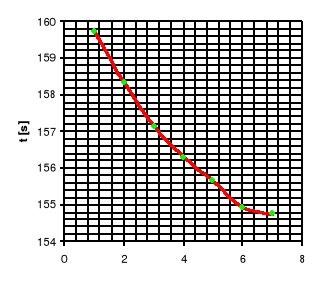
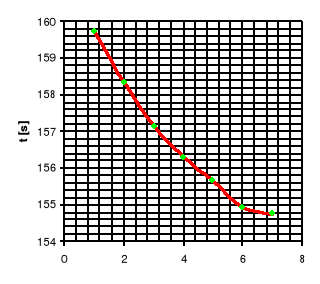
Pomiar współczynnika lepkości wiskozymetrem Höpplera jest obarczony mniejszym błędem niż pomiar w szerokim naczyniu. Wynika to z faktu, że na błąd wyznaczonego współczynnika składa się tylko błąd pomiaru czasu i błąd wyznaczenia gęstości kulki. Przy pomiarze czasu można zauważyć, że im więcej razy kulka przemieszcza się między kreskami, tym czas potrzebny na przebycie tej odległości jest mniejszy. Jest to zależne od tego, że w wyniku tarcia kulki o ciecz temperatura badanej cieczy wzrasta, co automatycznie pociąga za sobą zmianę współczynnika lepkości.

Z przedstawionego obok wykresu zależności czasu opadania od ilości pomiarów można w przybliżeniu zobaczyć jak zmienia się współczynnik lepkości cieczy w zależności od temperatury, ponieważ wykres ten ma podobny kształt do zależności (T), która jest opisana wzorem
, gdzie C, b są stałymi charakteryzują-cymi ciecz.

---