ILOCZYN ROZPUSZCZALNOŚCI

W roztworze nasyconym (pozostającym w równowadze z fazą nie rozpuszczoną) w danej temperaturze ustala się stan równowagi, w którym w jednostce czasu tyle samo substancji ulega rozpuszczeniu, co i wykrystalizowaniu. Jeżeli w roztworze znajduje się trudno rozpuszczalna substancja, to taki roztwór nasycony jest roztworem o bardzo małym stężeniu, które z dobrym przybliżeniem jest równe aktywności. Dla takiego procesu można napisać:

Dla powyższej reakcji wyrażenie na stałą równowagi przybierze postać:

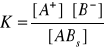
z czego:

K · [AB_s] = [A⁺] · [B^-]

Iloczyn dwóch stałych jest wielkością stałą. Oznaczając K · [AB_s] = I_r można napisać:

I_r = [A⁺] · [B^-].

Iloczyn [A⁺] · [B^-] nosi nazwę iloczynu rozpuszczalności i jest w danej temperaturze wielkością stalą i charakterystyczną dla danej substancji (trudno rozpuszczalnej).

Z analizy wyrażenia na iloczyn rozpuszczalności wynika, że jeżeli układ znajduje się w stanie równowagi i zwiększy się stężenie anionów, to spowoduje to zmniejszenie się stężenia kationów i na odwrót. Fakt ten jest wyko­rzystywany przy reakcjach „strąceniowych", w których używa się nadmiaru odczynnika strącającego, powodując tym samym dokładniejsze wytrącenie się jonów znajdujących się pierwotnie w roztworze (podstawa analizy wagowej strąceniowej).

Inną wielkością określającą rozpuszczalność danego elektrolitu w danej temperaturze jest rozpuszczalność molowa S, podająca, ile moli danej substancji rozpuszcza się w l dm³ roztworu pozostającego w równowadze z fazą nie rozpuszczoną.

Pomiędzy rozpuszczalnością molową a iloczynem rozpuszczalności istnieje ścisła zależność. Jeżeli dany związek chemiczny tworzy w roztworze jony, zgodnie z równaniem:
, to z równania reakcji wynika, że stężenie molowe każdego z jonów będzie równe stężeniu molowemu substancji znajdującej się w roztworze.

[AB] = [A⁺] = [B^-]. W związku z tym można napisać:

I_r = S², gdyż S = [AB] = [A⁺] = [B^-]

W przypadku związku chemicznego, złożonego z większej liczby jonów, można napisać:

A₂B₃ ↔ 2 A³⁺ + 3 B^2-

z powyższego równania wynika, że z jednego mola związku chemicznego powstają dwa mole jonów A³⁺ i trzy mole jonów B^2-, czyli stężenie jonów [A³⁺] = 2S, natomiast stężenie jonów [B^2-] = 3S.

W związku z powyższym wyrażenie na iloczyn rozpuszczalności przybierze postać:

I_r = (2S)²(3S)³

Po wykonaniu obliczeń otrzymuje się:

I_r=108S⁵.

Przeprowadzając podobne rozumowanie dla soli składającej się z innej liczby jonów niż w podanych przypadkach, można wyliczyć zależność po między iloczynem rozpuszczalności a rozpuszczalnością molową, która jest równa stężeniu molowemu roztworu. Przekształcając wyrażenie na rozpuszczalność molową, można na podstawie znajomości iloczynu rozpuszczalności obliczyć stężenie molowe danej substancji zawartej w określonej objętości roztworu.

Rozpuszczalność związków chemicznych określa się często podając liczbę gramów danej substancji, która rozpuści się w 100 g rozpuszczalnika w danej temperaturze.

Znając iloczyn rozpuszczalności lub rozpuszczalność molową oraz gęstość roztworu nasyconego, można obliczyć rozpuszczalność danej substancji.

Gęstość wodnych roztworów o bardzo małym stężeniu niewiele różni się od jedności (gęstość wody). Dlatego dla obliczeń o niewielkiej dokładności pomiaru i dla roztworów soli o małym iloczynie rozpuszczalności można przyjąć gęstość roztworu równą 1.

Tego rodzaju obliczenia są w wielu przypadkach przybliżone, gdyż nie uwzględniają hydrolizy soli oraz innych procesów chemicznych. Przy rozwiązywaniu zadań zawartych w tym zbiorze należy stosować uproszczenia i nie uwzględniać wpływu wspomnianych powyżej procesów na końcowy wynik zadania.

Przykład l

Obliczyć molową rozpuszczalność chlorku srebra. Rozwiązanie:

AgCl_s ↔ Ag⁺ + Cl^-

dla tego typu soli: I_r = S²,

po odczytaniu wartości I_r z tablic i podstawieniu, 1,56 ·10^-10 = S²

S = 1,25·10^-5 mola·dm^-3.

Odpowiedź: Molowa rozpuszczalność chlorku srebra wynosi 1,25·10^-5 mola·dm^-3.

Przykład 2

Obliczyć, ile gramów bromku srebra znajduje się w 3 dm³ nasyconego roztworu bromku srebra.

Rozwiązanie:

AgBr_s ↔ Ag⁺ + Br^-

I_r = S²

S = 6,32·10^-7 mola·dm^-3.

Jeżeli w l dm³ nasyconego roztworu znajduje się 6,32·10^-7 mola AgBr, to w 3 dm³ nasyconego roztworu będzie się znajdować x moli AgBr,

z czego x= 18,97·10^-7 = 1,9·10^-6.

Jeżeli masa l mola AgBr wynosi 188 g,

to masa 1,9·10^-6 mola AgBr będzie wynosiła z proporcji y g, z czego y = 3,87 ·10^-4 g.

Odpowiedź: W 3dm³ nasyconego roztworu bromku srebra znajduje się 3,87 ·10^-4 g tej soli.

Przykład 3

W jakiej objętości rozpuści się 3,7 ·10^-4 g bromku miedzi(I)? Rozwiązanie:

CuBr ↔ Cu⁺ + Br^-

Jeżeli masa l mola CuBr wynosi 143,45 g,

to masa x moli CuBr będzie wynosić 3,7 ·10^-3 g,

I_r CuBr = 4,1 ·10^-8

S = 2,02·10^-4 mola·dm^-3

Jeżeli w 1000 cm³ nasyconego roztworu znajduje się 2,02·10^-4 mola CuBr, to w x cm³ nasyconego roztworu będzie się znajdować 2,58 ·10^-5 mola CuBr,

z czego

Odpowiedź: Dla rozpuszczenia 3,87 ·10^-4 g bromku miedzi(I) potrzeba 127,7 cm³ wody (różnica między objętością otrzymanego roztworu a objętością wody potrzebnej do rozpuszczenia tej ilości soli jest tak mała, że można ją pominąć).

Przykład 4

Obliczyć, ile gramów siarczku arsenu(III) znajduje się w 700 cm³ nasyconego roztworu tej soli.

Rozwiązanie:

I_r = (2S)²·(3S)³

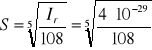
S = 8,2·10^-7 mola·dm^-3.

W celu obliczenia piątego pierwiastka z jakiejś liczby należy do kalkulatora wprowadzić daną liczbę znajdującą się pod pierwiastkiem następnie wcisnąć klawisz oznaczony SHIFT (w niektórych kalkulatorach przycisk ten może być oznaczony: Shift lub INV albo 2ndF) a następnie nacisnąć klawisz oznaczony: y^x, po czym wprowadzić liczbę 5 i nacisnąć klawisz oznaczony =. Na ekranie zostanie wyświetlona obliczana wartość liczbowa. Podobnie oblicza się wartości innych pierwiastków (np.: 3 lub 4, z tym, że zamiast 5 wpisuje się 3 lub 4).

Jeżeli masa l mola As₂S₃ wynosi 246,02 g,

to masa 8,2·10^-7 mola będzie wynosiła x g,

z czego x = 2,02·10^-4 g.

Jeżeli w 1000 cm³ nasyconego roztworu As₂S₃ znajduje się 2,02·10^-4 g,

to w 700 cm³ nasyconego roztworu As₂S₃ będzie się znajdować y g,

z czego

Odpowiedź: W 700 cm³ nasyconego roztworu siarczku arsenu(III) znajduje się 1,41·10^-4 g tej soli.

Przykład 5

Obliczyć, ile razy jest mniejsza rozpuszczalność (w g · dm^-3) bromku srebra w roztworze bromowodoru o stężeniu 0,07 mola · dm^-3, niż w wodzie.

Rozwiązanie:

Z przykładu 2 wiadomo, że rozpuszczalność molowa AgBr w wodzie wynosi = 6,32·10^-7 mola·dm^-3. Rozpuszczalność molowa w roztworze z dodatkiem HBr zostaje określona przez S₁. Stężenie jonów Br^- będzie równe stężeniu soli w roztworze plus stężenie jonów Br^- pochodzących z roztworu HBr. Natomiast stężenie jonów Ag⁺ będzie równe stężeniu soli w roztworze. Wobec powyższego można napisać:

I_r = S₁·(S₁+0,07)

Wartość S₁ w nawiasie można pominąć, ponieważ rozpuszczalność soli, a tym samym stężenie pochodzących z niej jonów Br^- jest bardzo małe w porównaniu ze stężeniem jonów Br^- pochodzących z HBr. Wobec czego można napisać:

I_r = S₁·0,07

po podstawieniu za I_r wartości z tablic:

4,0· 10^-l3 = 0,07S₁

Porównując wartość S z S₁ widać, że S₁ jest 10⁵ razy mniejsze niż S.

Odpowiedź: Rozpuszczalność bromku srebra w roztworze HBr o stężeniu 0,07 mola·dm^-3 jest 10⁵ razy mniejsza niż w wodzie.

Przykład 6

Wiedząc, że rozpuszczalność bromku miedzi(I) jest 400 razy mniejsza w roztworze bromowodoru niż w wodzie, obliczyć stężenie roztworu bromowodoru.

Rozwiązanie:

Ze znajomości iloczynu rozpuszczalności odczytanego z tabel oblicza się rozpuszczalność molową CuBr. Wynosi ona 2,02· 10^-4 mola · dm^-3 (patrz przykład 3). Jeżeli w roztworze bromowodom jest ona 400 razy mniejsza, to znaczy, że wynosi ona 5,05· 10^-7 mola · dm^-3. Przeprowadzając rozumowanie podobnie jak w poprzednim przykładzie, otrzymuje się:

I_r = S₁ ·(S₁ +x); x - stężenie bromowodoru S₁ jest wielkością bardzo małą w porównaniu z x i dlatego można ją pominąć. Po podstawieniu za S₁ i I_r otrzymuje się:

4,1· 10^-8 = 5,05·10^-7 ·x

Odpowiedź: W roztworze bromowodoru o stężeniu 0,08 mola · dm^-3 rozpuszczalność CuBr jest 400 razy mniejsze niż w wodzie.

Przykład 7

Zmieszano ze sobą 120 cm³ roztworu AgNO₃ o stężeniu 3· 10^-4 mola · dm^-3 z 450 cm³ roztworu HCl o stężeniu 9· 10^-5 mola · dm^-3. Obliczyć, ile gramów osadu wytrąci się w tym roztworze.

Rozwiązanie:

Najpierw należy obliczyć jakie byłoby stężenie poszczególnych związków chemicznych w roztworze, gdyby nie nastąpiło wytrącenie osadu w roztworze otrzymanym przez zmieszanie.

Jeżeli w 1000 cm³ znajduje się 0,0003 mola AgNO₃,

to w 120 cm³ będzie się znajdować x moli AgNO₃,

z czego

Jeżeli w 570 cm³ otrzymanego roztworu znajduje się 3,6· 10^-5 mola AgNO₃, to w 1000 cm³ otrzymanego roztworu będzie się znajdować y moli

z czego

Jeżeli w 1000 cm³ znajduje się 0,00009 mola HCl

to w 450 cm będzie się znajdować z moli HCl,

z czego

Jeżeli w 570 cm³ otrzymanego roztworu znajduje się 4,05 ·10^-5 mola HCl, to w 1000 cm³ otrzymanego roztworu będzie znajdowało się a moli HCl,

z czego

Do reakcji użyto więcej moli HCl niż AgNO₃.

Ilość moli rozpuszczonego w l dm³ roztworu AgNO₃ będzie równa rozpuszczalności molowej (S) i takie będzie stężenie jonów Ag⁺.

Stężenie jonów Cl^- będzie równe ilości moli HCL wprowadzonego do roztworu, pomniejszonego o ilość moli jonów Cl^-, które wytrąciły się z roztworu w postaci AgCl.

Jeżeli w l dm³ znajduje się S moli jonów Ag⁺, to w postaci osadu będzie związane (6,32 ·10^-5 - S) moli jonów Ag⁺; taka sama ilość moli jonów Cl^- będzie związana w wytrąconym osadzie. W związku z tym stężenie jonów Cl^- w roztworze będzie wynosiło:

[7,1 ·10^-5 - (6,32 ·10^-5 - S)]. Dlatego też:

I_r = S [7,10 ·10^-5 - (6,32 ·10^-5 - S)]. Po podstawieniu za I_r wartości liczbowej odczytanej z tablic i po wykonaniu działań po prawej stronie rów­ności, otrzymuje się:

1,56 ·10^-10 - S(7,8 ·10^-6 + S), z czego

S² + 7,8 ·10^-6 S - 1,56 ·10^-10 = 0; po rozwiązaniu równania II-go stopnia otrzymuje się:

S= 9,18 ·10^-6 mola ·dm^-3.

Liczba moli jonów Ag⁺, które wytrącą się w postaci osadu, jest równa liczbie moli AgCl zawartych w tym osadzie. Dlatego liczba moli AgCl znaj­dujących się w osadzie będzie wynosiła: 6,32 ·10^-5 - S; po podstawieniu wartości liczbowej za S:

liczba moli AgCl w osadzie = 6,32·10^-5 - 9,18 ·10^-6 = 5,4 ·10^-5 mola · dm^-3.

Jeżeli masa l mola AgCl wynosi 143,32 g,

to masa 5,4 ·10^-5 mola będzie wynosić b g,

z czego

Powyższa liczba gramów chlorku srebra wytrąciłaby się, gdyby w wyniku zmieszania roztworów powstało 1000 cm³ roztworu. Jeżeli otrzymalibyśmy 1000 cm³ roztworu, to wytrąciłoby się 7,74 ·10^-3 g AgCl.

Gdy otrzymano 570 cm³ roztworu, to wytrąciło się c g AgCl,

z czego

Odpowiedź: Po zmieszaniu ze sobą 120 cm³ roztworu AgNO₃ o stężeniu 3 ·10^-4 mol · dm^-3 z 450 cm³ roztworu HCl o stężeniu 9 ·10^-5 mol · dm^-3 wytrąci się 4,41 ·10^-3 g AgCl.

Przykład 8

Obliczyć rozpuszczalność wyrażoną w gramach KClO₄ w wodzie, zakładając, że gęstość roztworu jest równa 1 g/cm³.

Rozwiązanie:

I_r = S², po odczytaniu z tablic otrzymuje się:

1,07·10^-2 = S²

S = 0,103 mola KClO₄ w l dm³ roztworu.

Jeżeli masa l mola KClO₄ wynosi 138,55 g, to masa 0,103 mola KClO₄ wyniesie x g,

po obliczeniu: x = 14,27 g KClO₄ w l dm³ roztworu.

Przy założeniu, że gęstość roztworu jest równa l, w 1000 g roztworu znajduje się 14,27 g soli i 985,73 g wody.

Z definicji rozpuszczalności wiadomo, że jest to ilość gramów substancji, która rozpuści się w 100 g rozpuszczalnika.

Jeżeli w 985,73 g wody rozpuszcza się 14,27 g soli,

to w 100 g wody rozpuści się y g soli,

Po wyliczeniu : y=1,45 g

Odpowiedź: Rozpuszczalność chloranu(VII) potasu wynosi 1,45 g.

Zadania

Uwaga:

Jeżeli w zadaniach nie podaje się rozpuszczalnika, oznacza to, że rozpuszczalnikiem w danym roztworze jest woda. Potrzebne do rozwiązywania zadań wartości stałych dysocjacji i iloczynów rozpuszczalności należy odczytać z tabel.

1. Obliczyć rozpuszczalność molową TlCl.

2. Obliczyć rozpuszczalność molową Bi₂S₃.

3. Obliczyć, ile gramów CuCl znajduje się w 2300 cm³ nasyconego roztworu tej soli.

4. Obliczyć, ile gramów fluorku wapnia znajduje się w 750 cm³ nasyconego roztworu tej soli.

5. Obliczyć, w jakiej objętości wody rozpuści się 0,0219 g wodorotlenku wapnia.

6. W jakiej objętości wody rozpuści się 0,0136 g AgBO₂?

7. Obliczyć, ile razy mniejsza jest rozpuszczalność molowa TlCl w kwasie solnym o stężeniu 0,02 mola · dm^-3 niż w wodzie. (Przy względnie dużej wartości I_r nie można zaniedbać ilości jonów wspólnych pochodzących z dysocjacji soli).

8. Obliczyć, ile razy mniejsza jest rozpuszczalność molowa CaF₂: w roztworze HF o stężeniu 0,03 mola · dm^-3 niż w wodzie.

9. Obliczyć, jakie powinno być stężenie kwasu siarkowego(VI), aby rozpuszczalność molowa siarczanu(VI) wapnia była 320 razy mniejsza niż w wodzie.

10. Obliczyć, jakie powinno być stężenie wodorotlenku sodu, aby rozpuszczalność molowa wodorotlenku wapnia była 15000 razy mniejsza niż w wodzie.

11. Obliczyć w gramach rozpuszczalność siarczanu(VI) wapnia.

12. Obliczyć w gramach rozpuszczalność wodorotlenku wapnia.

13. 4,63 ·10^-4 g siarczku arsenu(III) rozpuściło się w 2300 cm³ wody. Obliczyć iloczyn rozpuszczalności tej soli w wodzie.

14. Obliczyć pH nasyconego roztworu wodorotlenku wapnia.

15. Czy po zmieszaniu 50 cm³ roztworu chlorku wapnia o stężeniu 0,01 mola · dm^-3 z 2 cm³ roztworu kwasu siarkowego(VI) o stężeniu 0,01 mola · dm^-3 wytraci się osad?

16. Jakie powinno być stężenie molowe kwasu solnego, aby po zmieszaniu 20 cm³ tego kwasu z 30 cm³ roztworu azotanu(V) srebra o stężeniu 2· 10^-5 mola · dm^-3 rozpoczęło się wytrącanie osadu?

17. Ile cm³ roztworu H₂SO₄ o stężeniu 0,056 mola potrzeba użyć, aby wytrącić osad z 45 cm³ nasyconego roztworu wodorotlenku wapnia?

18. Obliczyć, ile gramów osadu wytrąci się, jeżeli zmieszamy 20 cm³ roztworu chlorowodoru o stężeniu 0,0025 mola · dm^-3 z 50 cm³ roztworu TlNO₃ o stężeniu 0,01 mola · dm^-3.

19. Obliczyć w ppm stężenie jonów cyjankowych w nasyconym roztworze cyjanku srebra.

20. Obliczyć, ile gramów wodorotlenku wapnia pozostanie w l dm³ roztworu, powstałym przez dodanie do roztworu azotanu wapnia wodorotlenku sodu, tak że pH otrzymanego roztworu wynosi 12,9.

21. Przy jakiej wartości pH zacznie wytrącać się osad wodorotlenku wapnia w roztworze soli wapnia o stężeniu 0,01 mola · dm^-3?

22. Ile gramów osadu otrzyma się działając 200 cm³ roztworu kwasu siarkowego(VI) o stężeniu 0,012 mola · dm^-3 na 250 cm³ nasyconego roztworu wodorotlenku wapnia?

ROZTWORY BUFOROWE

Mianem roztworów buforowych określa się roztwory, które mają za zadanie utrzymywać stałe (lub dopuszczać tylko do minimalnych zmian) pH w czasie ich rozcieńczania lub dodawania do nich mocnych kwasów lub wodorotlenków. Roztworami buforowymi są mieszaniny: słabych kwasów i ich soli z mocnymi wodorotlenkami, słabych wodorotlenków lub zasad i ich soli z mocnymi kwasami lub dwóch wodorosoli tego samego kwasu.

W roztworze buforowym składającym się ze słabego kwasu i jego soli z mocnym wodorotlenkiem, można napisać wyrażenie na stałą dysocjacji tego kwasu:

ponieważ kwas HA jest słabym kwasem i w bardzo małym stopniu zdysocjowanym, dodanie soli cofa dysocjację kwasu, dlatego też można bez większego błędu przyjąć, że stężenie niezdysocjowanych cząsteczek kwasu będzie równe stężeniu wprowadzonego kwasu (ca). Natomiast jony A^- będą pochodziły głównie z soli, która ulega całkowitemu rozpadowi na jony i bez większego błędu można przyjąć, że ich stężenie będzie równe stężeniu wprowadzonej soli (c_s). W związku z powyższym można napisać:

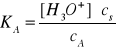
Po przekształceniu otrzymuje się:

Jak wynika z powyższego wyrażenia, stężenie jonów oksoniowych w tego typu roztworze buforowym jest zależne od stałej dysocjacji kwasu i stosunku liczby moli kwasu do liczby moli soli znajdujących się w roztworze, natomiast nie jest zależne od stężenia roztworu.

W związku z tym, wyrażenie na stężenie jonów oksoniowych przybierze postać:

gdzie n_A - liczba moli kwasu znajdująca się w pewnej objętości roztworu, a n_s - liczba moli soli znajdująca się w tej samej objętości tego roztworu.

W przypadku dodawania do takiego roztworu buforowego mocnego wodorotlenku. będzie zachodziła reakcja pomiędzy wodorotlenkiem a kwasem

HA + OH^- ↔ H₂O + A^-

Dodawane jony wodorotlenkowe, pochodzące z mocnego wodorotlenku, będą wiązane przez cząsteczki słabego kwasu, dając cząsteczkę wody i anion soli. Ponieważ powstająca sól w pewnym stopniu ulega hydrolizie, a słaby kwas jest też w pewnym stopniu zdysocjowany, stężenie jonów oksoniowych ulega zmianie w bardzo małym stopniu (gdyby nie zachodziła inna reakcja, tylko następowałoby wiązanie jonów OH^-, stężenie jonów oksoniowych nie ulegałoby zmianie).

Po dodaniuj mocnego kwasu zajdzje reakcja pomiędzy anionami soli a jonami oksoniowymi:

H₃O⁺ + A^- ↔HA + H₂O.

Dodawane jony oksoniowe pochodzące z mocnego kwasu będą wiązały się ż anionami słabego kwasu (pochodzącymi z soli), dając słabo zdysocjowane cząsteczki kwasu. Dlatego też, podobnie jak przy dodawaniu mocnego wodorotlenku, stężenie jonów oksoniowych będzie zmieniało się w bardzo małym stopniu. W przypadku rozcieńczania roztworu stężenie jonów oksoniowych nie będzie ulegało zbytniej zmianie, gdyż wraz z rozcieńczaniem zawartego w roztworze kwasu, dysocjacji będą ulegały niezdysocjowane dotychczas cząsteczki tego kwasu.

Podobny tok rozumowania można przeprowadzić dla roztworów buforowych składających się ze słabego wodorotlenku i jej soli pochodzącej od mocnego kwasu. Wyrażenie na stałą równowagi w tym roztworze można zapisać:

Ponieważ [B⁺] jest równe stężeniu wprowadzonej do roztworu soli (c_s), a stężenie BOH będzie równe stężeniu wprowadzonej do roztworu wodorotlenku (cb), otrzymuje się:

W tego typu roztworze buforowym stężenie jonów wodorotlenkowych jest zależne od stałej dysocjacji wodorotlenku oraz od stosunku liczby moli wodorotlenku znajdujących się w roztworze do liczby moli soli znajdujących się w roztworze; nie jest natomiast zależne od stężenia roztworu. W związku z powyższym wyrażenie na stężenie jonów wodorotlenkowych w roztworze buforowym przybierze postać:

gdzie n_B - liczba moli wodorotlenku znajdująca się w pewnej objętości roztworu, a n_s - liczba moli soli znajdująca się w tej objętości roztworu.

Po dodaniu mocnego wodorotlenku jony wodorotlenkowe będą wiązane przez kationy pochodzące z soli odtwarzając słaby wodorotlenek.

B⁺ + OH → BOH.

W związku z tym stężenie jonów wodorotlenkowych zawartych w roztworze będzie ulegało małej zmianie. Powstająca sól ulega hydrolizie w pewnym stopniu, a znajdujący się w roztworze wodorotlenek, będący wprawdzie słabym elektrolitem, jest również w pewnym stopniu zdysocjowany.

Dodany do roztworu buforowego mocny kwas będzie reagował ze słabym wodorotlenkiem, dając sól.

H₃O⁺ + BOH →B⁺ + 2H₂O.

W związku z powyższym, stężenie jonów wodorotlenkowych w roztworze będzie ulegało zmianie w bardzo małym stopniu, podobnie jak w przypadku dodawania mocnego wodorotlenku.

W przypadku rozcieńczania roztworu, dysocjacji będą ulegały niezdysocjowane dotychczas cząsteczki wodorotlenku, dzięki czemu stężenie jonów wodorotlenkowych praktycznie nie ulega zmianie.

Innego rodzaju roztworem buforowym jest roztwór, w skład którego wchodzą dwie wodoroście o tych samych anionach i kationach. Przykładem takiego roztworu buforowego jest mieszanina NaH₂PO₄ i Na₂HPO₄. W roztworze tym rolę soli spełnia jednowodorofosforan(V) sodu, a rolę kwasu dwuwodorofosforan(V) sodu, gdyż w wyniku dysocjacji (drugi stopień dysocjacji H₃PO₄) anionu H₂PO₄^-2 tworzą się jony oksoniowe (dysocjację HPO₄^- można praktycznie pominąć ze względu na bardzo mały, trzeci stopień dysocjacji w porównaniu z drugim). W związku z powyższym wyrażenie na stężenie jonów oksoniowych w takim roztworze przybierze postać:

gdzie c₁ - stężenie dwuwodorosoli, c₂ - stężenie jednowodorosoli, K_2A -stalą drugiego stopnia dysocjacji kwasu (np. H₃PO₄).

Ponieważ stężenie jonów oksoniowych nie zależy od stężeń soli znajdujących się w roztworze, a jedynie od stałej dysocjacji i stosunku liczby moli jednej wodorosoli do drugiej, można napisać:

gdzie n₁ - ilość moli dwuwodorosoli, a n₂ - ilość moli jednowodorosoli znajdujących się w pewnej objętości roztworu.

Dodając do roztworu buforowego kwasu lub wodorotlenku należy pamiętać, że wielkość zmiany pH będzie zależała od ilości dodanego kwasu lub wodorotlenku oraz od stężenia składników mieszaniny buforowej.

Najczęściej sporządzanymi roztworami buforowymi są:

bufor octanowy o zakresie pH 3,5 - 6 (CH₃COOH + CH₃COONa),

bufor amonowy o zakresie pH 8 - 10 (NH₃ + NH₄CI),

bufor fosforanowy o zakresie pH 4,8 - 8 (NaH₂PO₄ + Na₂HPO₄)

bufor węglanowy o zakresie pH 1 0,2 - 1 1 (NaHCO₃ + Na₂CO₃),

bufor boranowy o zakresie pH 7,7 - 1 1 (H₃BO₃ + Na₂B₄O₇).

Przykład l

Obliczyć pH mieszaniny buforowej powstałej przez zmieszanie 500 cm³ roztworu octanu sodu o stężeniu 0,2 mola · dm^-3 z 500 cm³ roztworu kwasu octowego o stężeniu 0,3 mola · dm^-3.

Rozwiązanie:

Do roztworu wprowadzono 0,1 mola octanu sodu (jeżeli w 1000 cm roztworu znajduje się 0,2 mola, to w 500 cm³ będzie się znajdować 0,1 mola) i 0,15 mola kwasu octowego. Wyrażenie na stężenie jonów oksoniowych w takim roztworze będzie miało postać:

[H₃O] = 2,62 ·10^-5 mola · dm^-3

pH = - log 2,62 ·10^-5

pH = 4,58

Odpowiedź: pH powstałej mieszaniny buforowej wynosi 4,58.

Przykład 2

Ile cm³ należy dodać roztworu chlorku amonu o stężeniu 0,3 mola · dm^-3 do 300 cm³ roztworu amoniaku o stężeniu 0,1 mola · dm^-3, aby pH otrzymanego roztworu wynosiło 8,7?

Rozwiązanie:

Jeżeli pH roztworu wynosi 8,7, to jego pOH będzie wynosiło 5,3, zaś

[OH^-] = 5,01 ·10^-6 mola · dm^-3.

Jeżeli w 1000 cm³ roztworu znajduje się 0,1 mola NH₃,

to w 300 cm³ roztworu będzie się znajdować x moli NH₃,

z czego x = 0,03 mola,

Po podstawieniu danych do wyrażenia na stężenie jonów wodorotlenkowych w tego typu mieszaninie buforowej otrzymuje się:

y = 0,107 mola.

Jeżeli w 1000 cm³ znajduje się 0,3 mola NH₄Cl,

to w z cm³ będzie się znajdować 0,107 mola NH₄Cl,

z czego z = 367 cm³.

Odpowiedź: Do 300 cm³ roztworu amoniaku o stężeniu 0,1 mola · dm^-3 należy dodać 367 cm³ roztworu chlorku amonu o stężeniu 0,3 mola · dm^-3, aby otrzymać mieszaninę o pH 8,7.

Przykład 3

Obliczyć, o ile mniej jednostek zmieni się pH 100 cm³ roztworu buforu fosforanowego zawierającego 2,11 ·10^-3 mola KH₂PO₄ i 1,33 ·10^-3 mola mola K₂HPO₄ w 100 cm³ roztworu w porównaniu do 100 cm³ wody, jeżeli do obydwu próbek dodamy po 10 cm³ roztworu HCl o stężeniu 0,1 mola · dm^-3. Rozwiązanie:

pH= 7,00.

W 10 cm³ rotworu HCl o stężeniu 0,1 mola · dm^-3 znajduje się 0,001 mola chlorowodoru.

Po dodaniu do roztworu buforu roztworu kwasu solnego ilość KH₂PO₄ zwiększy się o 0,001 mola a ilość K₂HPO₄ zmniejszy się o 0,001 mola i nowe ilości moli tych soli będą odpowiednio wynosiły: 0,00311 i 0,00033 mola. Stężenie jonów oksoniowych w nowo otrzymanym roztworze będzie wynosiło:

pH = 6,22

7-6,22 = 0,78

Po dodaniu do 100 cm³ wody 10 cm³ roztworu kwasu solnego o stężeniu 0,1 mola · dm^-3 otrzyma się 110 cm³ roztworu zawierającego 0,001 mola HCl.

Jeżeli w 110 cm³ znajduje się 0,001 mola HCl, to w 1000 cm³ będzie znajdowało się x moli HCl,

x = 9,1 ·10^-3 mola · dm^-3.

Ponieważ kwas solny jest mocnym kwasem, stężenie jonów oksoniowych będzie więc równe stężeniu HCl.

pH= -log 9,1 ·10^-3

pH = 2,04.

Po dodaniu HCl do wody pH zmieni się o 4,96 (7,00 - 2,04) jednostki.

Po dodaniu do mieszaniny buforowej tej samej ilości kwasu solnego pH zmieniło się o 0,78 jednostek. Dlatego w przypadku zastosowania mieszaniny buforowej zmiana pH będzie mniejsza o 4,18 (4,96 - 0,78) jednostek niż w przypadku wody.

Odpowiedź: Po dodaniu 10 cm³ kwasu solnego o stężeniu 0,1 mola · dm^-3 do 100 cm³ wody i 100 cm³ mieszaniny buforowej zmiana pH mieszaniny buforowej będzie o 4,18 jednostek mniejsza niż zmiana pH wody.

Przykład 4

Obliczyć, ile cm³ roztworu wodorotlenku sodu o stężeniu 0,8 mola · dm^-3 należy dodać do 400 cm³ roztworu kwasu octowego o stężeniu 0,25 mola · dm^-3, aby otrzymać roztwór buforowy o pH = 4,45.

Rozwiązanie:

pH = 4,45

[H₃O⁺] = 3,55 ·10^-5 mola · dm^-3.

Jeżeli w 1000 cm³ roztworu kwasu octowego znajduje się 0,25 mola CH₃COOH,

to w 400 cm³ roztworu kwasu octowego będzie się znajdować x moli CH₃COOH,

z czego x - 0,1 mola.

W wyniku reakcji kwasu octowego z wodorotlenkiem sodu powstaje octan sodu. Ilość moli soli będzie równa ilości moli dodanego wodorotlenku sodu. Jeżeli liczbę moli soli oznaczymy przez y, to liczba moli kwasu będzie równa (0,1 - y). Po podstawieniu danych do wyrażenia na stężenie jonów oksoniowych w roztworze buforowym otrzymuje się:

Dokonując kolejnych przekształceń otrzymuje się:

y = 0,033 mola.

Jeżeli w 1000 cm³ roztworu znajdowało się 0,8 mola NaOH, to w a cm³ będzie się znajdować 0,033 mola NaOH,

z czego a = 41,2 cm³.

Odpowiedź: Aby z 400 cm³ roztworu kwasu octowego o stężeniu 0,25 mola · dm^-3 otrzymać roztwór buforowy o pH = 4,45, należy dodać do niego 41,2 cm³ roztworu wodorotlenku sodu o stężeniu 0,8 mola · dm^-3.

Przykład 5

Obliczyć, o ile zmieni się pH, jeżeli do 700 cm³ roztworu zawierającego po 9 g wodorofosforanu(V) potasu i dwuwodorofosforanu(V) potasu dodano l cm³ roztworu wodorotlenku sodu o stężeniu l mola · dm^-3.

Rozwiązanie:

Jeżeli masa l molaK₂HPO₄ wynosi 174,18 g,

to masa x moli będzie wynosić 9 g,

z czego x = 0,0517 mola K₂HPO₄

Jeżeli masa l mola KH₂PO₄ wynosi 136,09 g,

to masa y moli będzie wynosić 9 g,

z czego y = 0,0661 mola KH₂P0₄

pH = 7,09.

Po dodaniu do tego roztworu l cm³ roztworu NaOH o stężeniu l mola · dm^-3, liczba moli KH₂PO₄ zmaleje o 0,001 (ilość moli NaOH, które przereagują z KH₂PO₄ dając NaKHPO₄) i będzie wynosiło 0,0661 - 0,001 = 0,0651 mola. Liczba moli jednowodorosoli wzrośnie o 0,001 i będzie wynosiło 0,0517 + 0,001 = 0,0527 mola.

Stężenie jonów oksoniowych w otrzymanym roztworze będzie wynosiło:

pH = 7,11

7,11-7,09 = 0,02.

Odpowiedź: W badanym roztworze buforu fosforanowego po dodaniu do niego l cm³ roztworu NaOH o stężeniu l mola · dm^-3 pH wzrośnie o 0,02 jednostki.

Przyklad 6

Obliczyć, jaką objętość powinien posiadać roztwór buforu amonowego, w którym stężenie amoniaku wynosi 0,95 mola · dm^-3, pH - 8,85, aby po dodaniu do niego 30 cm³ roztworu kwasu azotowego(V) o stężeniu 0.3 mola · dm^-3 jego pH obniżyło się o 0,09 jednostki.

Rozwiązanie:

pH = 8,85

pOH = 5,15

[OH^-] = 7,08 ·10^-6 mola · dm^-3.

Z wyrażenia na stężenie jonów wodorotlenkowych w tego rodzaju buforze otrzymuje się:

x = 2,4 mola NH₄Cl w 1 dm³ roztworu.

Po dodaniu mocnego kwasu pH roztworu obniży się, a pOH wzrośnie i będzie wynosiło: 5,15+0,09 = 5,24 jednostki, stąd OH^- = 5,75 ·10^-6 mola · dm^-3.

Znając stężenie jonów wodorotlenkowych, można obliczyć stosunek liczby moli amoniaku do liczby moli chlorku amonu w nowym roztworze. Zakładając, że po dodaniu kwasu w pewnej objętości otrzymuje się:

y = 3,1.

Jeżeli w 1000 cm³ kwasu solnego znajdowało się 0,3 mola HCl, to w 30 cm³ będzie się znajdować z moli HCl,

z czego z = 0,009 mola.

Za a przyjmuje się ilość moli amoniaku znajdujących się w V cm³ roztworu przed dodaniem kwasu.

Jeżeli w l dm³ roztworu znajduje się 0,95 mola amoniaku, to w V cm³ roztworu będzie się znajdować a moli amoniaku, z czego a = 0,95 · V moli NH₃ w roztworze buforu amonowego. Przeprowadzając podobne rozumowanie dla liczby moli chlorku amonu w tym roztworze buforowym, otrzymuje się:

b = 2,4 · VmolaNH₄Cl.

Po dodaniu 0,009 mola kwasu azotowego(V) liczba moli amoniaku zmniejszy się o 0,009 i będzie wynosiło a - 0,009 mola. Natomiast liczba moli chlorku amonu będzie wynosiło b + 0,009 mola.

Wiadomo, że po dodaniu kwasu stosunek ilości moli amoniaku do ilości moli chlorku amonu wynosił: 1:3,1 w związku z czym można napisać, że

(a - 0,009) : (b + 0,009) = l : 3,1;

po podstawieniu za a i b wyliczonych wcześniej wartości otrzymuje się:

(0,95 · V - 0,009) : (2,4 · V + 0,009) = 1:3,1.

Po wyliczeniu proporcji:

3,1 - 0,95V - 3,1 · 0,009 = 2,4V + 0,009

z czego V - 0,06709 dm³ = 67,09 cm³.

Odpowiedź: Bufor amonowy powinien posiadać objętość 67,09 cm³ .

Zadania

Uwaga:

Jeżeli w zadaniach nie podaje się rozpuszczalnika, oznacza to, że rozpuszczalnikiem w danym roztworze jest woda. Wartości stałej dysocjacji oraz gęstości roztworów, potrzebne do rozwiązywania zadań, należy odczytać z tabeli.

1. Jakie będzie pH roztworu po rozpuszczeniu w wodzie 0,3 mola kwasu octowego i 0,5 mola octanu sodu?

2. Ile będzie wynosiło pH roztworu powstałego przez zmieszanie 300 cm roztworu amoniaku o stężeniu 0,4 mola· dm^-3 z 250 cm³ roztworu chlorku amonu o stężeniu 0,3 mola·dm^-3?

3. Obliczyć, ile będzie wynosiło pH roztworu, jeżeli w 900 cm³ wody rozpuszczono 15 g octanu sodu i 10 g kwasu octowego.

4. Ile moli Na₂HPO₄ należy zmieszać z 0,2 molami NaH₂PO₄, otrzymać roztwór, którego pH wynosi 6,83?

5. Ile cm³ roztworu amoniaku o stężeniu 0,15 mola · dm^-3 należy dodać do 450 cm³ roztworu chlorku amonu o stężeniu 0,097 mola · dm^-3, aby jego pH wynosiło 9,74?

6. Obliczyć, ile gramów Na₂HPO₄ należy dodać do roztworu zawierającego 18 g NaH₂PO₄, aby jego pH wynosiło 7,92.

7. Ile będzie wynosiło pH roztworu powstałego przez rozpuszczenie w wodzie 0,3 mola kwasu octowego i 0,21 mola wodorotlenku sodu?

8. Obliczyć, ile będzie wynosiło pH roztworu powstałego przez zmieszanie 450 cm³ roztworu amoniaku o stężeniu 0,3 mola · dm^-3 z 200 cm³ roztworu kwasu solnego o stężeniu 0,25 mola · dm^-3 .

9. Obliczyć, ile będzie wynosiło pH roztworu powstałego przez rozpuszczenie w wodzie 20 g kwasu octowego i 10 g wodorotlenku sodu.

10. Obliczyć pH roztworu powstałego przez zmieszanie 60 g l %-owego roztworu kwasu octowego z 300 cm³ octanu potasu o stężeniu 2,032 g · dm^-3.

11. Ile moli kwasu ortofosforowego(V) należy dodać do roztworu zawierającego 0,12 mola K₂HPO₄, aby otrzymać roztwór buforowy, którego pH wynosi 7,82?

12. Obliczyć, ile cm³ roztworu wodorotlenku sodu o stężeniu 0,3 mola · dm^-3 należy dodać do 500 cm³ roztworu kwasu octowego o stężeniu 0,65 mola · dm^-3, aby otrzymać roztwór buforowy o pH = 3,95.

13. Ile gramów kwasu solnego należy dodać do roztworu zawierającego 15 g węglanu sodu, aby uzyskać roztwór buforowy o pH = 10,40 (w reakcji tej należy uwzględnić drugi stopień dysocjacji kwasu węglowego)?

14. O ile zmieni się pH roztworu buforowego zawierającego 0,06 mola Na₂HPO₄ i 0,03 mola NaH₂PO₄, jeżeli doda się do niego 0,01 mola NaOH?

15. Do roztworu buforowego o pH = 5,42, zawierającego 0,02 mola kwasu octowego, dodano 50 cm³ roztworu HCl o stężeniu 0,02 mola · dm^-3. Obliczyć, o ile zmieni się pH roztworu.

16. Do 200 cm³ roztworu Na₂CO₃ o stężeniu 0,2 mola · dm^-3 dodano roztworu kwasu solnego i otrzymano roztwór buforowy o pH = 10,22. O ile zmieni się pH roztworu buforowego jeśli dodano 0,2 g wodorotlenku sodu?

17. Obliczyć, o ile zmieni się pH roztworu buforu fosforanowego, powstałego przez zmieszanie 250 g 3%-owego NaH₂PO₄ z 300 cm³ roztworu, w którym stężenie Na₂HPO₄ wynosi 24,25 g· dm^-3 jeżeli doda się do niego 3,2 cm³ wodorotlenku sodu o mianie 0,0032 g· cm^-3. O ile zmieniłoby się pH, gdyby do takiej samej objętości wody co otrzymany roztwór, dodać tyle samo, takiego samego roztworu NaOH?

18. Obliczyć pH roztworu, w którym ułamek molowy octanu sodu wynosi 0,009, a kwasu octowego 0,007.

19. Ile moli kwasu solnego należy dodać do roztworu buforowego, zawierającego 0,06 mola K₂HPO4 i 0,03 mola KH₂PO₄, aby zmienić pH roztworu buforowego o 0,21 jednostki?

20. Ile cm³ roztworu wodorotlenku sodu o stężeniu 0,3 mola · dm^-3 należy dodać do roztworu buforowego powstałego przez zmieszanie 300 cm³ roztworu amoniaku o stężeniu 0,3 mola · dm^-3 z 250 cm³ roztworu chlorku amonu o stężeniu 0,2 mola · dm^-3, aby zmienić jego pH o 0,15 jednostki?

21. Ile gramów 58%-owego kwasu azotowego(V) należy dodać do 450 cm³ roztworu buforowego, w którym stężenie octanu sodu wynosi 0,02 mola · dm^-3, a pH = 4,23, aby stężenie jonów oksoniowych wzrosło dwukrotnie.

22. Jak zmieni się ułamek molowy soli w 700 g roztworu buforu fosforanowego, powstałego przez zmieszanie 4 g NaH₂PO₄ z 3 g Na₂HPO₄, gdy po dodaniu do niego 30 g roztworu HCl pH zmieniło się o 0,11 jednostki?

23. Jaka będzie różnica pH roztworów buforowych po dodaniu do nich po 2 cm³ roztworu NaOH o stężeniu 0,9 mola · dm^-3? W obydwu roztworach stosunek molowy CH₃COOH do CH₃COOK wynosi 1:1. W jednym roztworze znajduje się 0,004 mola kwasu octowego, a w drugim 0,01.

24. Obliczyć, jakie będzie pH roztworu, jeżeli do 350 cm³ roztworu kwasu azotowego(V) o stężeniu 0,25 mola · dm^-3 zostanie wprowadzone i 6,37 dm³ amoniaku.

25. Obliczyć stężenie octanu potasu i kwasu octowego w roztworze buforowym o pH = 4,62, jeżeli po dodaniu do 750 cm³ tego roztworu 25 cm³ roztworu NaOH o stężeniu 0,07 mola · dm^-3 jego pH wzrosło o 0,15 jednostki.

26. Obliczyć, w jakim stosunku wagowym należy zmieszać 20%-owy kwas solny z 15%-owym roztworem amoniaku, aby otrzymać roztwór buforowy o pH = 8,34.

27. W jednym roztworze buforowym stężenie kwasu octowego wynosi 0,1 mola · dm^-3, a jego pH = 3,7, w drugim roztworze buforowym stężenie octanu sodu wynosi 0,2 mola · dm^-3, a pH = 4,9. Obliczyć pH roztworu otrzymanego przez zmieszanie 300 cm³ pierwszego i 500 cm³ drugiego roztworu.

28. Ile gramów octanu sodu należy uzyć aby otrzymać roztwor buforowy o pH = 4,77, z 300 cm³ roztworu kwasu octowego o stężeniu 0,1 mola · dm^-3_, wiedząc że po dodaniu do niego 70 cm³ roztworu kwasu solnego o stężeniu 0,15 mola · dm^-3 pH zmienia się o 0,23 jednostki?

29. Rozpuszczono w wodzie mieszaninę wodorofosforanu(V) potasu i dwuwodorofosforanu(V) potasu, otrzymując roztwór buforowy o pH = 6,96. Obliczyć skład procentowy mieszaniny fosforanów.

30. Po dodaniu 5 cm³ roztworu NaOH o stężeniu 0,075 mola · dm^-3 do 200 cm³ roztworu buforu amonowego, pH wynosiło 10,11. Obliczyć stężenie molowe chlorku amonu i amoniaku w tym roztworze buforowym, wiedząc że stężenie jonów NH₄⁺ wynosi 0,101 mola · dm^-3.

31. Do 200 cm³ roztworu kwasu solnego o stężeniu 0,07 mola · dm^-3 wprowadzono 600 cm³ amoniaku. Obliczyć, ile cm³ roztworu chlorku amonu o stężeniu 12 g · dm^-3 należy dodać do tego roztworu, aby jego pH zmieniło się o 0,09 jednostki.

32. Ile dm³ amoniaku zawierającego 8% (objętościowych) zanieczyszczeń azotem należy wprowadzić do 300 cm³ kwasu solnego o mianie 0,006 g · dm^-3, aby otrzymać roztwór buforowy, którego pH będzie wynosiło 9,15?

33. Jakie objętości gazowego chlorowodoru i amoniaku należy wprowadzić do 300 cm³ roztworu wodorotlenku sodu o stężeniu 0,03 mola · dm^-3, aby pH otrzymanego roztworu wynosiło 9,52, a stężenie jonów Cl^- = 0,2%?

34. Ile cm³ roztworu jednowodorofosforanu(V) potasu o stężeniu 0,07 mola · dm^-3 należy zmieszać z roztworem dwuwodorofosforanu(V) potasu o stężeniu 0,06 mola · dm^-3, aby po dodaniu do niego 7 cm³ roztworu KOH o stężeniu 0,27 mola · dm^-3 pH z 7,4 wzrosło do 7,82?

35. Ile dm³ CO₂ należy wprowadzić do 200 cm³ roztworu wodorotlenku sodu i jakie powinien mieć ten roztwór stężenie, aby po dodaniu do niego 25 cm³ kwasu solnego o stężeniu 0,12 mola · dm^-3 pH z 10,52 obniżyło się na 10,37.

20

---