![]()
Średnia statystyczna
Statystyka wzory
![]()
Średnia statystyczna
![]()
- suma wszystkich składników
N - liczebność składników
Wi = ![]()
częstość względna po * 100% otrzymamy udział w %
ni - dana liczba ni
n - suma wszystkich ni
Skni = wynik Skni + ni
Skwi = ![]()
D = Xmax ni wartość najczęstsza - występuje tam gdzie jest najwięcej ni wtedy gdy nie ma przedziału.
Dominanta w równych przedziałach:
D = xd + ![]()
Xd - dolna granica przedziału z dominantą
nd - liczebność przedziału z dominantą
nd-1 - liczebność przedziału poprzedzającego przedział z dominantą
nd+1 - liczebność przedziału po przedziale z dominantą
![]()
Xd - długość przedziału z dominantą
gi = ![]()
- gęstość liczebności ![]()
- długość przedziału (gdy przedziały są nierówne)
D = xd + ![]()
Mediana Me = ![]()
= X np. 0,50*N = X……. - Znaleźć najbliższą liczbę w Skni
Q0,25 - kwantyl 1
Q0,75 - kwantyl 3
Me =![]()
= ![]()
+![]()
![]()
Q - kwantyl
Xβ - dolna granica przedziału z kwantylem
B*N - numer obserwacji który jest kwantylem
F* - skumulowana liczebność Skni w przedziale poprzedzającym przedział z kwantylem.
Nβ - liczebność ni przedziału z kwantylem
![]()
- długość przedziału z kwantylem
Gdy nie na przedziałów
Wariancja S2 = ![]()
S = ![]()
![]()
Odchylenie standardowe
WZ = ![]()
współczynnik zmienności ale ![]()
Jeżeli wynik z Wz zawiera się między:
(0%-20%) - zróżnicowanie słabe
(20%-40%) - zróżnicowanie przeciętne
(40%-60%) - zróżnicowanie wysokie
powyżej 60% - zróżnicowanie wysokie
![]()
- środek (średnia) wybranego przedziału
Gdy są liczby
S2 = ![]()
Wz = ![]()
ale ![]()
Gdy przedziały są równe
S2 = ![]()
Wz = ![]()
ale ![]()
Gdy przedziały są nierówne
Odchylenie ćwiartkowe
Q = ![]()
Wz = ![]()
Me =![]()
= ![]()
+![]()
![]()
Mierniki asymetrii:
Współczynnik asymetrii Pirsona AP = ![]()
Współczynnik asymetrii Yulla Kendalla AS = ![]()
Wykład
Yt = a1t + a0
Q1 = 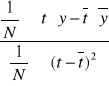
a0 = ![]()
Wariancja resztowa
![]()
Odchylenie standardowe reszt:
![]()
Współczynnik zmienności
![]()
Współczynnik zgoności
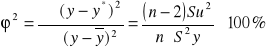
Współczynnik determinacji
![]()
![]()
oraz d wyrażone są w %
p - cena
q - ilość
o - okres bazowy (dawniejszy)
n - okres badany (świeższy)
![]()
![]()
Zespołowy indeks wartości
![]()
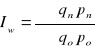
Zespołowy indeks zmiany cen Laspeyres-a
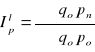
Zespołowy indeks cen Passchego
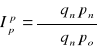
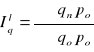
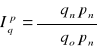
Równości indeksowe
![]()
![]()
Współczynnik korelacji Pirsona:
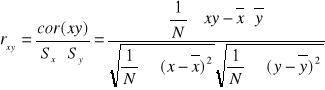
![]()
cor(xy) - suma po wymnożeniu wszystkich średnich i podzielona przez liczebność średnich N. Od tego odejmujemy iloczyn średnich i dzielimy to wszystko przez iloczyn Sx i Sy.
![]()
![]()
![]()
![]()
Średnia łączna ilość
Analiza regresji - ocenia o ile średnio rzecz biorąc zmienia się wartość zmiennej y gdy zmienna niezależna x wzrośnie o jednostkę.
![]()
![]()
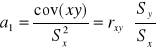
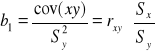
![]()
![]()
Miarą dokładności z jaką linie regresji opisują związek między zmiennymi jest współczynnik determinacji:
![]()
Współczynnik korelacji RANG:
Czy między powierzchnią, a ceną zachodzi zależność? x - powierzchnia y - cena
Vx - rosnąca kolejność wg x
![]()
![]()
Współczynnik Czuprowa: ![]()
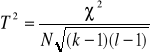
gdzie 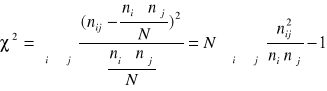
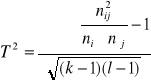
![]()
k- liczba wyróżnionych
![]()
![]()
![]()
1-α - poziom ufności (bliskie 0)
uα - wartość, wielkość odczytana z tablic rozkładu normalnego.
tα - wartość, wielkość odczytana z tablic rozkładu w wierszu n - 1 i w kolumnie α
1- α |
uα |
0,90 |
1,64 |
0,95 |
1,96 |
0,99 |
2,58 |
![]()
![]()
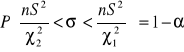
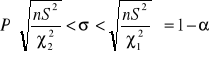
![]()
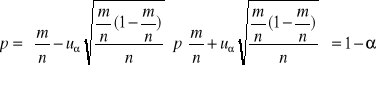
![]()
- z tablic rozkładu ![]()
wiersz n - 1 kolumna ![]()
![]()
- wiersz n-1 kolumna ![]()
H0 - hipoteza sprawdzalna
H1 - hipoteza alternatywna
H0 : ![]()
H1 : ![]()
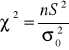
H0 : p = p0
H1 : p ![]()
p0
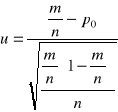
H0 : u = u0
H1 : u ![]()
u0
n > 30
a.) ![]()
![]()
b.) ![]()
H0 : p1 = p2
H1 : p1 ![]()
p2
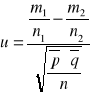
![]()
; q = 1 - p
![]()
![]()
H0 : ![]()
H1 : ![]()
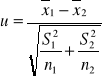
n1 > 30
n2 > 30
H0 : ![]()
H1 : ![]()
![]()