LABOLATORIUM FIZYKI 1			ĆWICZENIE NR. 0
Wydział: SiMR	Grupa: 2.1.	Zespół: 5	Data: 14.10.98
Nazwisko i imię:			ocena	Przygotowanie:
Temat ćwiczenia: Sprawdzanie Prawa Ohma					Zaliczenie:

Celem ćwiczenia było sprawdzenie Prawa Ohma (U = RI ) przy jednoczesnym uwzględnieniu błędu pomiaru .

Na początku ćwiczenia został wykonany układ elektryczny (rys.1).

Rys.1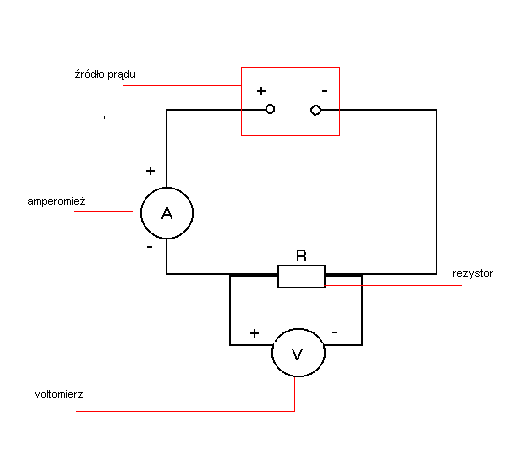

Następnie wykonaliśmy 10 pomiarów napięcia i natężenia prądu przy stałej rezystancji. Oto wyniki pomiarów:

lp.	I [A]	U [V]	R [ ]
1	0	0	0
4	0,042	4	190,4762
3	0,032	6	187,5
5	0,054	8	185,1852
2	0,022	10	181,8182
6	0,064	12	187,5
7	0,076	14	184,2105
8	0,084	16	190,4762
9	0,094	18	191,4894
10	0,106	20	188,6792

Przy pomocy programu „nkwadrat” który realizuje metodę najmniejszej sumy kwadratów policzyliśmy błąd dla powyższych pomiarów. Program „nkwadrat” umożliwuia określenie błędu kiedy mierzone wielkości fizyczne związane są zależnością liniową lub przez odpowiednie podstawienie można taką zależność otrzymać. W naszym przypadku mamy do czynienia z funkcją liniową ;

U = R I

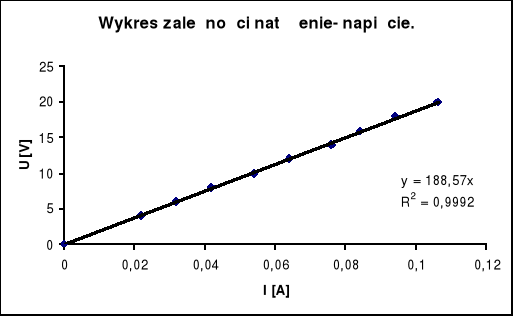
Następnie program naniósł otrzymane wartości rezystancji na układ współrzędnych i za pomocą najmniejszej sumy kwadratów aproksymował wykres. Otrzymaliśmy wykres:

Metoda najmniejszych kwadratów wyznacza dopasowanie punktów do linii reprezentowanej przez następujące równanie ;

y = mx + b

gdzie : y- wartość napięcia , m- rezystancja , x - natężenie prądu , b=0 wyraz wolny. Z wykresu odczytujemy wartość rezystancji ;

Następnie za pomocą metody pochodnej logarytmicznej obliczyliśmy wartość rezystancji dla piątego pomiaru.

U = 8 [V]

I = 0,054 [A]

R = 185,1852

Korzystając ze wzoru:

obliczam

a zatem z metody pochodnej logarytmicznej otrzymujemy

Wniosek: Ponieważ pomiary na amperomierzu były odczytywane z dokładnością co do jedności i do obliczeń wykorzystany został wynik znacznie odbiegający od prostej aproksymującej błąd pojedynczego pomiaru nie mieści się w granicach błędu obliczonego metodą najmniejszej sumy kwadratów.

1

1