PRZEDZIAŁ UFNOŚCI DLA WARTOŚCI OCZEKIWANEJ

Przedziałem ufności - nazywamy taki przedział, który z zadanym z góry prawdopodobieństwem
zwanym poziomem ufności lub współczynnikiem ufności, pokrywa nieznaną wartość szacowanego parametru.

to poziom istotności

Konstruowanie przedziału ufności dla wartości przeciętnej m:

Jeżeli mamy dużą próbę (n>30) oraz cecha X ma rozkład normalny X ~ N(m,
) , wówczas przedział ufności dla parametru m ma postać:

gdzie:

- średnia arytmetyczna,

- odchylenie standardowe, założenie (
)

n- liczebność próby,

m - wartość oczekiwana (przeciętna),

- wartość krytyczna odczytana z tablic rozkładu normalnego, gdzie:

Przykład:

Zakładając, że kwartalne wydatki na reklamę można uznać za cechę o rozkładzie normalnym, wylosowano 100 zakładów usługowych i otrzymano następujący rozkład wydatków na reklamę:

0-5	10	2,5	25	-9,5	90,25	902,5
5-10	20	7,5	150	-4,5	20,25	405
10-15	40	12,5	500	0,5	0,25	10
15-20	30	17,5	525	5,5	30,25	907,5
-	100	-	1200	-	-	2225

Wyznaczyć na poziomie ufności
przedział ufności dla przeciętnych kwartalnych wydatków na reklamę.

Najpierw obliczamy średnią arytmetyczną dla szeregu rozdzielczego przedziałowego:

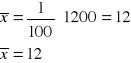
Następnie obliczamy wariancję S²:

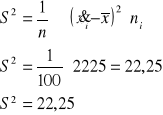
Teraz obliczamy odchylenie standardowe, czyli pierwiastek z wariancji:

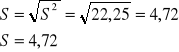
Zakładamy, że

Następnie z tablic rozkładu normalnego odczytujemy wartość
, przy czym
, zatem
.

Podstawiamy wszystko do wzoru:

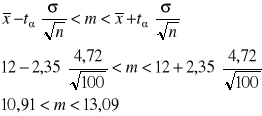
Odp. Z prawdopodobieństwem 98% ten przedział pokrywa wartość przeciętną m.

TESTOWANIE HIPOTEZY DLA WARTOŚCI OCZEKIWANEJ

Testowanie hipotez statystycznych obejmuje zasady i metody sprawdzania określonych przypuszczeń (założeń), dotyczących parametrów lub postaci rozkładu cech statystycznych populacji generalnej na podstawie wyników z próby prostej.

Hipotezą statystyczną - nazywamy każdy sąd o zbiorowości generalnej, wydany bez przeprowadzenia badania całkowitego, prawdziwość hipotezy statystycznej orzeka się na podstawie próby losowej.

Hipoteza zerowa H0 - hipoteza sprawdzana (testowana, weryfikowana).

Hipoteza alternatywna H1 - hipoteza, którą można przyjąć, gdy zostanie odrzucona hipoteza zerowa H0.

Sprawdzianem hipotezy - (zwanym też statystyką testową) jest taka zmienna losowa T, o znanym rozkładzie, której wartość empiryczna temp., policzona na podstawie próby losowej, pozwala na podjęcie decyzji, czy przyjąć, czy też odrzucić hipotezę H0.

Zbiór krytyczny Z - jest to zbiór tych wartości sprawdzianu hipotezy, które przemawiają za odrzuceniem hipotezy H0. W zależności od hipotezy może być zbiorem jednostronnym (prawostronnym lub lewostronnym) albo zbiorem dwustronnym.

Przeprowadzanie testu polega na weryfikacji hipotez - stawiamy hipotezę zerową (H₀) i hipotezę alternatywną (H₁). Ważna jest ich postać, bo przy np. innej postaci H₁ mamy inny test i inną konkluzję, - więc postaci hipotez trzeba dokładnie wypisać. Następnie potrzebujemy postaci tzw. sprawdzianu testu, - czyli statystyki testowej - zmiennej losowej, dla której wartość realizacji możemy wyliczyć korzystając z posiadanych danych i na tej podstawie wnioskować o hipotezach. Możemy to zrobić, ponieważ znamy rozkład statystyki testowej przy prawdziwości hipotezy zerowej - to jeden z zasadniczych elementów testu. Następnie badamy, jak ma się uzyskana realizacja statystyki testowej do tego rozkładu. Jeżeli uzyskujemy realizację z obszaru wysokiego prawdopodobieństwa, świadczy to, że H₀ MOŻE być prawdziwa - nie udało się temu zaprzeczyć - zaobserwowaliśmy zdarzenie, które jest bardzo prawdopodobne przy prawdziwości H₀.

Jednak nie możemy bezpośrednio wnioskować, że H₀ jest prawdziwa - musielibyśmy wiedzieć, że statystyka testowa przy fałszywości hipotezy zerowej ma rozkład przypisujący niskie prawdopodobieństwo zaobserwowanej wartości statystyki. Konkluzja testu brzmi wobec tego „NIE MA PODSTAW DO ODRZUCENIA H₀”.

Inaczej jest, gdy zaobserwujemy realizację statystyki testowej z obszaru niskiego prawdopodobieństwa w rozkładzie statystyki przy prawdziwości H₀ (tzw. obszaru krytycznego) - wnioskujemy wtedy, że gdyby prawdziwa była H₀, to musiałoby zajść bardzo mało prawdopodobne zdarzenie. Przypuszczamy, że to się raczej nie stało, że obserwujemy realizację z INNEGO rozkładu niż ten przy prawdziwości H₀, więc że H₀ nie jest prawdziwa. W tym wypadku konkluzja brzmi - ODRZUCAMY H₀ i PRZYJMUJEMY H₁. Zauważmy, że taka konkluzja jest bardziej konkretna niż w pierwszym przypadku.

Czyli w dużym skrócie - konkluzja się zmienia w zależności od tego, czy uzyskana wartość statystyki testowej wpada do obszaru krytycznego (odrzucamy H₀) czy nie (nie ma podstaw do odrzucania H₀).

Warto zawsze przyjrzeć się konstrukcji statystyki testowej - na tej podstawie można wyrobić sobie intuicję, jakie (np. duże czy małe) wartości statystyki odpowiadają prawdziwości H₁ a jakie są niesprzeczne z prawdziwością H₀.

Jak jednak określa się, co to znaczy „mało prawdopodobne”, - czyli: Jak dokładnie konstruuje się obszar krytyczny, jak wyznacza się jego granice?

Na samym początku ustalamy, tzw. poziom istotności (oznaczany zwykle alfa), - czyli prawdopodobieństwo fałszywego odrzucenia prawdziwej hipotezy zerowej. To jest określenie, co uznajemy za „mało prawdopodobne” - godzimy się z tym, że np. błędnie odrzucimy prawdziwą hipotezę zerową raz na 20 przypadków (wtedy
=0,05) lub raz na 100 (
=0,01). Z rozkładu statystyki testowej wyznaczamy zbiór wartości zmiennej taki, że „odcinamy” pod funkcją gęstości dokładnie alfa prawdopodobieństwa - oczywiście nie wszystko jedno, jak, lecz tak, był to obszar odpowiadający „jak najlepiej” zaprzeczeniu H₀, czyli prawdziwości hipotezy alternatywnej. Granica obszaru krytycznego to tzw. wartość krytyczna. Porównujemy ją ze zrealizowaną (wyliczoną na podstawie zaobserwowanych danych) wartością statystyki i wyprowadzamy konkluzję testu.

Postacie hipotezy alternatywnej:

1)
jest to dwustronny obszar krytyczny, dla którego

t

0

Gdzie:
- wartość krytyczna odczytana z tablic rozkładu normalnego.

2)
jest to lewostronny obszar krytyczny, dla którego

t

0

3)
jest to prawostronny obszar krytyczny, dla którego

t

0

Tryb postępowania przy weryfikacji:

1. Sformułowanie hipotez.

2. Wybór sprawdzianu hipotezy (jest uzależniony od n, czyli liczebności próby oraz od tego, czy
   jest znane).

Jeżeli
jest znane i
lub
znane i n>30 lub
nieznane i n>30 (wtedy
), wtedy sprawdzianem hipotezy zerowej jest statystyka:

o rozkładzie normalnym N(0,1)

3) Rysujemy wykres funkcji rozkładu normalnego i zaznaczamy obszar krytyczny, w zależności od postaci hipotezy alternatywnej. Następnie na wykresie zaznaczamy wartość
obliczoną z powyższego wzoru na T.

Jeżeli uzyskana wartość statystyki testowej
wpada do obszaru krytycznego, wówczas odrzucamy hipotezę H₀ na korzyść H₁. Jeżeli
nie wpada do obszaru krytycznego, to nie ma podstaw do odrzucenia H₀, czyli hipotezę zerową przyjmujemy za prawdziwą.

Przykład 1 (zad. 5 z listy nr 8):

Zbadano w 81 wylosowanych zakładach pewnej gałęzi przemysłowej koszty materiałowe przy produkcji pewnego wyrobu i otrzymano średnią
zł oraz
zł. Na poziomie istotności
zweryfikować hipotezę, że średnie koszty materiałowe przy produkcji tego wyrobu wynoszą 600 zł.

Dane:

;
zł - średnia arytmetyczna ;
zł - odchylenie standardowe ;
- poziom istotności ; 600 zł - średnie koszty materiałowe.

- Formułujemy hipotezę zerową oraz hipotezę alternatywną:

(a) hipoteza zerowa
, tzn., że średnie koszty materiałowe wynoszą 600 zł.

(b) hipoteza alternatywna
, tzn., że średnie koszty materiałowe nie wynoszą 600 zł.

Ponieważ hipoteza
, więc zbiór krytyczny jest dwustronny i dla rozkładu normalnego dla
mamy:
.

Teraz odczytujemy z tablic
.

Podstawiamy dane do wzoru na T:

t

-3,6
0

Ponieważ
wpada do obszaru krytycznego, wobec tego hipotezę
odrzucamy na korzyść hipotezy alternatywnej, co oznacza, że średnie koszty materiałowe nie wynoszą 600 zł.

Przykład 2:

Średnia życia mężczyzn w Polsce wynosi 67,5 lat. Interesuje nas obszar zagłębia legnicko-głogowskiego. Podejrzewamy, że z uwagi na duże zagrożenie ekologiczne, średnia życia jest tutaj niższa niż średnia krajowa. Wybrano losowo 238 mężczyzn i obliczono, że
oraz S=12,9. Na poziomie istotności 0,05 zweryfikować powyższą hipotezę.

Dane:

;
zł - średnia arytmetyczna; S=12,9zł - odchylenie standardowe;
- poziom istotności; 67,5 lat - średnia życia mężczyzn w Polsce (średnia krajowa).

- Formułujemy hipotezę zerową oraz hipotezę alternatywną:

(a) hipoteza zerowa
, tzn., że średnia życia jest równa średniej krajowej.

(b) hipoteza alternatywna
, tzn., że średnia życia jest niższa niż średnia krajowa.

Ponieważ hipoteza
, więc zbiór krytyczny jest lewostronny i dla rozkładu normalnego dla
mamy:
.

Teraz odczytujemy z tablic
.

Podstawiamy dane do wzoru na T:

t

-2,51
0

Ponieważ
wpada do obszaru krytycznego, wobec tego hipotezę
odrzucamy na korzyść hipotezy alternatywnej, co oznacza, że średnia życia na obszarze zagłębia legnicko-głogowskiego jest niższa niż średnia krajowa.

STATYSTYKA I RACHUNEK PRAWDOPODOBIEŃSTWA - ĆWICZENIA

LISTA ZADAŃ NR 8 - PRZEDZIAŁ UFNOŚCI I HIPOTEZY

Zad. 1 W 49 - elementowej próbie losowej robotników otrzymano
jednorodnych operacji wykonanych w ciągu 1 dnia, przy współczynniku zmienności 8%. Przyjmując poziom ufności 0,95 wyznaczyć metodą przedziałową przeciętną liczbę operacji.

Zad. 2 Dane dotyczące stażu pracy w zakładzie A są następujące:

Staż w latach	0 - 6	6 - 12	12 - 18	18 - 24
Liczba pracowników	10	20	40	30

Wyznaczyć przedział ufności dla przeciętnego stażu pracy pracowników tego zakładu, jeśli poziom ufności wynosi 0,95.

Zad. 3 W firmie „Telimena” zbadano 500 płaszczy spośród nowo wyprodukowanych partii i otrzymano następujący rozkład liczby usterek:

Liczba usterek	0	1	2	3	4	5
Liczba płaszczy	90	160	100	80	50	20

Wyznaczyć na poziomie ufności 0,95 przedział ufności dla przeciętnej liczby usterek w płaszczach produkowanych w badanej firmie.

Zad. 4 W celu oszacowania średniego czasu poświęconego tygodniowo przez studentów na naukę, wylosowano próbę 132 studentów i otrzymano w niej następujące wyniki:

Czas nauki (w h)	0-2	2-4	4-6	6-8	8-10	10-12
Liczba studentów	10	28	42	30	15	7

Przyjmując poziom ufności 0,90 oszacować metodą przedziałową średni tygodniowy czas nauki studentów.

Zad. 5 Zbadano w 81 wylosowanych zakładach koszty materiałowe produkcji pewnego wyrobu i otrzymano
i s=150. Na poziomie istotności α = 0,10, zweryfikuj hipotezę, ze średnie koszty materiałowe = 600.

Zad.6 Z populacji o rozkładzie normalnym N(m; 0,2) pobrano próbę czteroelementową: 1,14; 1,06; 1,13; 1,17. Na poziomie istotności
zweryfikować hipotezę, że m=1,05.

Zad. 7 Z próby 100 elementowej obliczono
i
. Na poziomie istotności 0,05 zweryfikować hipotezę
przeciw hipotezie
.

Zad. 8 W pewnym teście psychologicznym przeprowadzonym na wylosowanych 50 dzieciach otrzymano następujący rozkład wyników liczby zapamiętanych przez dzieci elementów:

Liczba elementów	15-20	20-25	25-30	30-35	35-40	40-45	45-50
Liczba dzieci	6	8	12	10	7	4	3

Sprawdzić hipotezę, że średnia liczba zapamiętanych przez dzieci elementów w teście wynosi 35. Przyjąć poziom istotności 0,02.

Zad. 9 Z populacji o rozkładzie normalnym N(m; 0,1) pobrano próbę trzyelementową: 1,12; 1,05; 1,13. Na poziomie istotności 0,01 zweryfikować hipotezę, że m=1,20 przeciw hipotezie
.

Państwowa Wyższa Szkoła Zawodowa im. Witelona w Legnicy

Specjalność: Sterowanie Systemami Przemysłowymi

mgr Iwona Czerska

e-mail: [e-mail]

1

---