Nr Ćwiczenia 3.	Temat Ćwiczenia Rezonans  akustyczny	Ocena z Teorii
Nr Zespołu 10.	Nazwisko i Imię	Ocena zaliczenia ćwiczenia
Data 11.04.06	Wydział Rok Grupa EAIiE 1 5	Uwagi

Fale dźwiękowe w gazach i ciałach stałych

Fala to zaburzenie, które się rozprzestrzenia w ośrodku lub przestrzeni. Fale przenoszą energię z jednego miejsca do drugiego bez transportu jakiejkolwiek materii.

Fale dźwiękowe - są podłużnymi falami mechanicznymi rozchodzącymi się w ośrodkach sprężystych: ciałach stałych, cieczach i gazach. Są to fale ciśnieniowe.

Ze względu na zakres częstotliwości wyróżnia się trzy rodzaje fal dźwiękowych:

infradźwięki - poniżej 20 Hz

dźwięki słyszalne 20 Hz - 20 kHz

ultradźwięki - powyżej 20 kHz

Falę dźwiękową opisuje równanie:

- amplituda drgań (maksymalne wychylenie)

- częstość kołowa drgań

- wektor falowy

Podstawowe pojęcia z akustyki

Każdy dźwięk przedstawić jako sumę drgań o określonych częstotliwościach (tw. Fouriera).

Ton to drgania z jedną częstotliwością

Słyszalność dźwięku zależy nie tylko od jego częstotliwości, ale od energii docierającej do ucha w jednostce czasu. Ucho ludzkie ma różną czułość dla różnych częstotliwości dźwięków. Najwyższa dla dźwięków o częstotliwości ok. 1-3kH.

Zjawiska akustyczne:

Echo - kilkukrotne usłyszenie dźwięku spowodowane kilkukrotnym odbiciem od odległej przeszkody

Pogłos - wielokrotne odbicie dźwięku w zamkniętym pomieszczeniu, słyszalne jako przedłużenie dźwięku

Zjawisko Dopplera - zmiana odbieranej częstotliwości fali na skutek ruchu źródła lub odbiornika

Dudnienia - okresowe zmiany amplitudy dźwięku wypadkowego

Interferencja fal

Polega na nakładaniu się fal, objawiające się wzmocnieniem lub osłabieniem fali.

Dla dwóch fal o jednakowych amplitudach i częstościach

- różnica faz fal

W wyniku interferencji powstaje nowa fala:

o amplitudzie

gdy
to następuje wzmocnienie (zgodne fazy fal), a gdy
wygaszenie (przeciwne fazy fal).

Fale stojące

Powstaje w wyniku interferencji dwóch fal o takich samych amplitudach i częstościach, ale rozchodzących się w przeciwnych kierunkach.

W doświadczeniu:

- fala z głośnika

- fala odbita od wody

- dodatkowa droga którą musi przejść fala odbita; L - wysokość słupa powietrza

w wyniku interferencji powstaje fala stojąca:

Gdy fala odbita dochodzi do głośnika w tej samej fazie, w której głośnik się znajduje, to fala przekazuje energię i następuje wzmocnienie natężenia dźwięku czyli rezonans.

Przy rezonansie w rurze powstaje fala stojąca z węzłem na powierzchni wody i strzałką przy wylocie z rury.

czyli dla

więc

Równanie spełnione w przypadku rezonansu. Mierząc L można wyznaczyć długość fali.

Prędkość dźwięku w gazach

Można wyznaczyć na podstawie częstotliwości fali ze wzoru:

- częstotliwość

- długość fali

Rozchodzenie się dźwięku w gazie polega na lokalnych zmianach zagęszczenia gazu, które zachodzą bardzo szybko i bez przepływu ciepła (tzw. przemiana adiabatyczna).

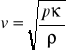
- gęstość ośrodka, w którym rozchodzi się fala

- moduł ściśliwości objętościowej dla gazu

- ciśnienie gazu

- stosunek ciepła właściwego przy stałym ciśnieniu do ciepła właściwego przy stałej objętości

Stopnie swobody

Liczbę niezależnych zmiennych opisujących jednoznacznie stan (modelu) układu fizycznego nazywa się liczbą Stopni swobody tego układu.

W mechanice klasycznej jest to liczba niezależnych ruchów, jakie ciało jest może wykonać w przestrzeni. Przez niezależnych rozumie się, że żaden z tych ruchów nie może być uzyskany poprzez superpozycję pozostałych.

Ciało sztywne całkowicie swobodne (to jest takie, na które nie nałożono żadnych więzów) ma maksymalną liczbę sześciu stopni swobody:

trzy ruchy translacyjne w stosunku do osi układu współrzędnych X, Y i Z. (ruch postępowy)

trzy obroty względem osi równoległych do osi układu współrzędnych X, Y i Z. (ruch obrotowy)

Ciała odkształcalne mogą posiadać większą liczbę stopni swobody.

W przypadku gazów do obliczenia liczby stopni swobody
cząsteczki można skorzystać ze wzoru:

1.

		Położenia wody w rezonansie
Powietrze
800	0,00125	8, 29, 51, 72, 94 9, 30, 51, 73, 94	21,375	42,75	0,4275
1000	0,001	6, 24, 42, 59, 77, 95 8, 24, 42, 60, 77, 96	17,7	35,4	0,354
1200	0,000833	5, 19, 34, 49, 63, 78, 93 5, 19, 34, 49, 63, 78, 94	14,75	29,5	0,295
1500	0,000667	15, 26, 38, 50, 61, 73, 85, 97 16, 27, 39, 50, 62, 74, 85, 97	11,643	23,286	0,23286
Dwutlenek Węgla
500	0,002	5, 18, 31, 44, 57, 70, 84, 97	26	52	0,52
1000	0,001	12, 37, 64, 90	13,143	26,286	0,26286

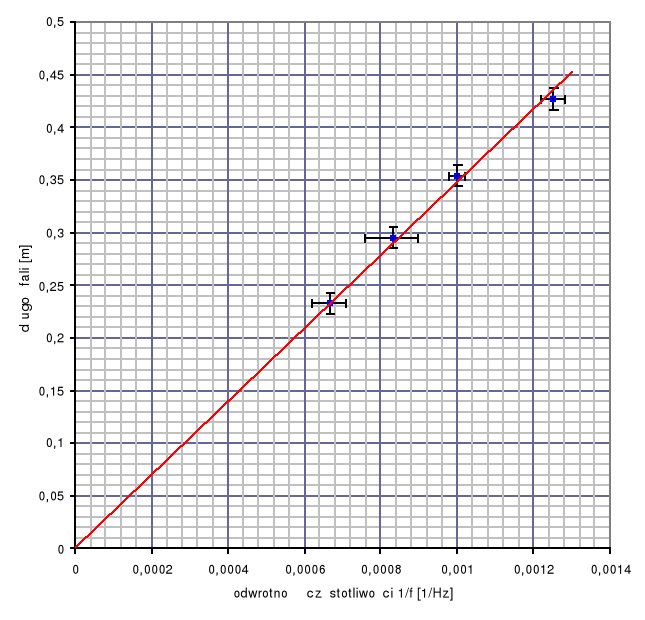
2a. Wykres zależności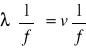
dla powietrza

2b. Wykres zależności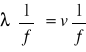
dla dwutlenku węgla

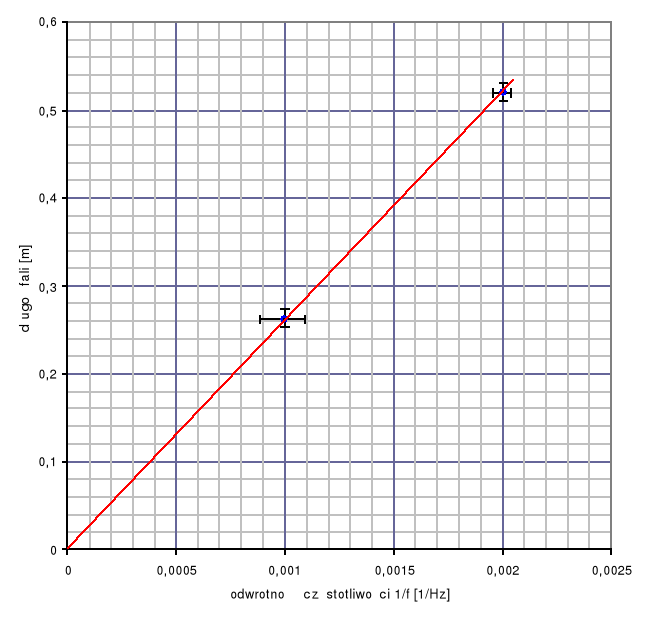
3 i 7.

Dla obu gazów metodą regresji liniowej wyznaczono proste najlepiej opisujące dane doświadczalne i przechodzące przez punkt (0,0).

Na podstawie tych prostych można wyznaczyć prędkość dźwięku w danym gazie, która jest równa współczynnikowi kierunkowemu prostej:

w powietrzu

w dwutlenku węgla

4 i 5.

Ze wzoru na prędkość dźwięku w gazie można obliczyć współczynnik
.

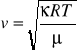
Następnie na podstawie współczynnika
można dla danego gazu określić liczbę stopni swobody
korzystając z zależności:

W doświadczeniu:		Powietrze	Dwutlenek węgla
Stała gazowa		8,3144
Temperatura gazu		295
Masa molowa gazu		0,028	0,044
Prędkość		348,37	260,57
Współczynnik		1,385	1,218
Liczba stopni swobody		5,189	9,174
Współczynnik (wartość teoretyczna)		1,4	1,3
Liczba stopni swobody (wartość teoretyczna)		5	6

8.

Obliczona liczba stopni swobody w przypadku powietrza nie odbiega znacząco od wartości teoretycznej. Natomiast dla dwutlenku w węgla wynik jest stanowczo za duży.

W tym doświadczeniu trudno jest uzyskać dużą dokładność liczby stopni swobody, ponieważ sposób obliczania wymaga bardzo dokładnego wyznaczenia prędkości dźwięku w gazie. We wzorze na współczynnik
prędkość jest podnoszona do kwadratu, a następnie obliczony współczynnik jest wykorzystywany w zależności na liczbę stopni swobody, w której niewielkie zmiany
przekładają się na duże zmiany
.

6.

Na dokładność wyznaczenia prędkości duży wpływ miało wyznaczenie długości fali. Doświadczenie polegało na znalezieniu położenia wody dla maksymalnego natężenia dźwięku, co jest dość trudne metodą „na oko” bez żadnego sprzętu pomiarowego. Wiec niepewność pomiarowa długości fali wyniosła ok. ±1 cm.

Niepewność pomiarowa częstotliwości wynika z podziałki na generatorze dźwięku. Podziałka nie jest liniowa, dlatego niepewność jest różna dla różnych częstotliwości:

,
,
,
,

Podziałka jest dość duża, więc można przyjąć, że niepewność pomiaru częstotliwości jest mniejsza.

Na wyznaczoną prędkość w dwutlenku węgla wpływ mogło mieć też to, gazu w rurze nie był czysty. Ponadto dla dwutlenku węgla zostały wykonane tylko dwie serie pomiarów, natomiast dla powietrza osiem, dlatego liczba stopni swobody powietrza wyznaczona w doświadczeniu jest dużo bliższa wartości teoretycznej.

5

---