Tabela nr 1. Zaległości w spłacie kredytu mieszkaniowego w zasobach spółdzielni mieszkaniowych w 1993 r.
Lp. |
Województwa |
Stopa bezrobocia w procentach |
1 |
Warszawskie |
6,5 |
2 |
Bialskopodlaskie |
14,1 |
3 |
Białostockie |
14,8 |
4 |
Bielskie |
10,3 |
5 |
Bydgoskie |
19,9 |
6 |
Chełmskie |
16 |
7 |
Ciechanowskie |
21,3 |
8 |
Częstochowskie |
11,8 |
9 |
Elbląskie |
25,1 |
10 |
Gdańskie |
14,6 |
11 |
Gorzowskie |
22,4 |
12 |
Jeleniogórskie |
19,4 |
13 |
Kaliskie |
17,5 |
14 |
Katowickie |
10 |
15 |
Kieleckie |
17,8 |
16 |
Konińskie |
19,8 |
17 |
Koszalińskie |
29,2 |
18 |
Krakowskie |
8,4 |
19 |
Krośnieńskie |
17,2 |
20 |
Legnickie |
19,7 |
21 |
Leszczyńskie |
14,5 |
22 |
Lubelskie |
14,7 |
23 |
Łomżyńskie |
15,8 |
24 |
Łódzkie |
19,5 |
25 |
Nowosądeckie |
15,5 |
26 |
Olsztyńskie |
24,5 |
27 |
Opolskie |
14,7 |
28 |
Ostrołęckie |
19,7 |
29 |
Pilskie |
22,9 |
30 |
Piotrkowskie |
19,4 |
31 |
Płockie |
19,5 |
32 |
Poznańskie |
8,4 |
33 |
Przemyskie |
17,3 |
34 |
Radomskie |
17,6 |
35 |
Rzeszowskie |
17,8 |
36 |
Siedleckie |
16,7 |
37 |
Sieradzkie |
15 |
38 |
Skierniewickie |
10,6 |
39 |
Słupskie |
29,8 |
40 |
Suwalskie |
25,4 |
41 |
Szczecińskie |
11,5 |
42 |
Tarnobrzeskie |
15,2 |
43 |
Tarnowskie |
10,9 |
44 |
Toruńskie |
21,9 |
45 |
Wałbrzyskie |
23,2 |
46 |
Włocławskie |
22,7 |
47 |
Wrocławskie |
10,5 |
48 |
Zamojskie |
14,2 |
49 |
Zielonogórskie |
18,2 |
Wstęp
Przedmiotem pracy jest analiza wielkości bezrobocia w poszczególnych województwach Polski w 1994r. Powyższe dane (Tablica nr1) pochodzą z Rocznika Statystycznego Polski wydanego przez GUS z roku 1995. Dane te zostały przedstawione za pomocą cechy ilościowej ciągłej.
SZEREG ROZDZIELCZY WIELOSTOPNIOWY
Aby ułatwić analizę i porównanie danych pogrupuję je w szereg rozdzielczy przedziałowy. Warianty ujęto w klasy.
Empiryczny obszar zmienności R to różnica między największą i najmniejszą wartością zmiennej w badanej zbiorowości:
R = xmax - xmin
R = 29,8 - 6,5 = 23.3
Liczba przedziałów klasowych k:
![]()
dla n = 49
k = 7
Rozpiętość przedziałów klasowych h:
![]()
h = 23,3 / 7
h = 3,3
Po dokonaniu powyższych obliczeń dokonano grupowania wariacyjnego (tabela nr 2). Dolną granicą pierwszego przedziału klasowego jest wartość minimalna cechy.
Tabela nr 2. Szereg rozdzielczy wielostopniowy
Klasa |
Stopa bezrobocia w procentach |
Województwa |
1 |
6,5 - 9,9 |
3 |
2 |
9,9 - 13,3 |
7 |
3 |
13,3 - 16,7 |
10 |
4 |
16,7 - 20,1 |
18 |
5 |
20,1 - 23,5 |
6 |
6 |
23,5 - 26,9 |
3 |
7 |
26,9 - 29,9 |
1 |
W celu dokonania wstępnej analizy rozkładu cechy, sporządzono histogram (wykres nr 1) i krzywą liczebności (wykres nr 2).
Wykres nr 1. Histogram
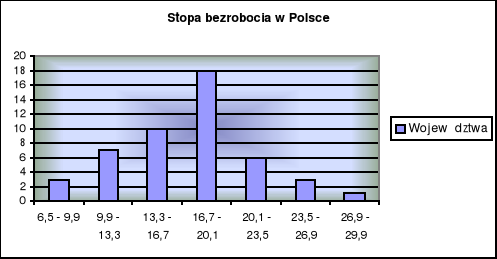
Wykres nr 2. Krzywa liczebności
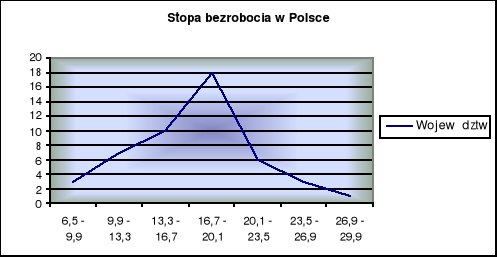
Na podstawie histogramu i krzywej liczebności można zauważyć, że rozkład jest asymetryczny (asymetria prawostronna), ma jedno maksimum. Domknięte przedziały klasowe pozwalają na zastosowanie miar klasycznych (odchylenia standardowego, wariancji oraz odchylenia przeciętnego).
MIARY ŚREDNIE
Miary średnie (zwane też miarami poziomu wartości zmiennej, miarami położenia lub miarami przeciętnymi) służą do określania tej wartości zmiennej opisanej przez rozkład, wokół której skupiają się wszystkie pozostałe wartości zmiennej.
Ponieważ szereg ma zamknięte przedziały klasowe obliczono średnią arytmetyczną.
Średnia arytmetyczna xśr to suma wartości zmiennej wszystkich jednostek badanej zbiorowości podzielona przez liczbę tych jednostek.
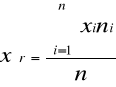
![]()
Do obliczenia średniej arytmetycznej niezbędne jest wyznaczenie środków przedziałów klasowych. Wyniki zamieszczono w tabeli nr 3.
Tabela nr 3. Szereg rozdzielczy wielostopniowy ze środkami przedziałów
Numer klasy |
Stopa bezrobocia w Polsce |
Środki przedziałów xi |
Liczba województw ni |
Iloczyn xini |
|
|
|
|
|
1. |
6,5 - 9,9 |
8,2 |
3 |
24,6 |
2. |
9,9 - 13,3 |
11,6 |
7 |
81,2 |
3. |
13,3 - 16,7 |
15 |
10 |
150 |
4. |
16,7 - 20,1 |
18,4 |
18 |
331,2 |
5. |
20,1 - 23,5 |
21,8 |
6 |
130,8 |
6. |
23,5 - 26,9 |
25,2 |
4 |
100,8 |
7. |
26,9 - 30,3 |
28,6 |
1 |
28,6 |
Suma |
- |
- |
49 |
847,2 |
Xśr = 847,2 / 49
Xśr = 17,3
Przeciętna stopa bezrobocia w Polsce w 1994 roku wynosi 17,3%
MIARY ROZPROSZENIA
Miary rozproszenia ( zwane też miarami zmienności, zróżnicowania lub dyspersji) służą do badania stopnia zróżnicowania wartości zmiennej.
Wariancja s2 to średnia arytmetyczna z kwadratów odchyleń poszczególnych wartości cechy od średniej arytmetycznej całej zbiorowości.
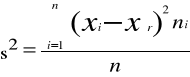
Tabela nr 5. Szereg rozdzielczy wielostopniowy z wartościami niezbędnymi do wyznaczenia odchylenia przeciętnego.
Numer klasy |
Stopa bezrobocia w Polsce |
Środki przedziałów xi |
Liczba województw ni |
xi-xśr |
(xi-xśr)2ni |
|
<xi0 - xi1) |
|
|
|
|
1. |
6,5 - 9,9 |
8,2 |
3 |
-9,1 |
248,43 |
2. |
9,9 - 13,3 |
11,6 |
7 |
-5,7 |
227,43 |
3. |
13,3 - 16,7 |
15 |
10 |
-2,3 |
52,90 |
4. |
16,7 - 20,1 |
18,4 |
18 |
1,1 |
21,78 |
5. |
20,1 - 23,5 |
21,8 |
6 |
4,5 |
121,50 |
6. |
23,5 - 26,9 |
25,2 |
4 |
7,9 |
249,64 |
7. |
26,9 - 30,3 |
28,6 |
1 |
11,1 |
127,69 |
Suma |
- |
- |
49 |
7,5 |
1049,37 |
S2 = 1094,37 / 49
s2 = 21,41
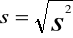
Odchylenie standardowe s określa, o ile wszystkie jednostki danej zbiorowości różnią się średnio od średniej arytmetycznej badanej zmiennej. Jest pierwiastkiem kwadratowym z wariancji:
S = 4,63
Stopa bezrobocia w Polsce w poszczególnych województwach różni się od średniej arytmetycznej przeciętnie o 4,63%.
Typowy obszar zmienności xtyp to obszar, w którym mieści się około 2/3 wszystkich jednostek badanej zbiorowości statystycznej. Jest on zawarty w granicach dwóch odchyleń standardowych.
xśr - s <xtyp < xśr + s
12,67<xtyp <21,93
2/3 procentowej stopy bezrobocia w poszczególnych województwach zawiera się w przedziale od 12,67% do 21,93%.
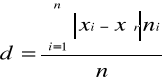
Odchylenie przeciętne d określa, o ile wszystkie jednostki danej zbiorowości różnią się średnio ze względu na wartość zmiennej od średniej arytmetycznej tej zmiennej.
Numer klasy |
Stopa bezrobocia w % |
Środki przedziałów xi |
Liczba województw ni |
xi-xśr |
xi-xśr ni |
|
<xi0 - xi1) |
|
|
|
|
1. |
6,5 - 9,9 |
8,2 |
3 |
-9,1 |
27,30 |
2. |
9,9 - 13,3 |
11,6 |
7 |
-5,7 |
39,90 |
3. |
13,3 - 16,7 |
15 |
10 |
-2,3 |
23,00 |
4. |
16,7 - 20,1 |
18,4 |
18 |
1,1 |
19,80 |
5. |
20,1 - 23,5 |
21,8 |
6 |
4,5 |
27,00 |
6. |
23,5 - 26,9 |
25,2 |
4 |
7,9 |
31,60 |
7. |
26,9 - 30,3 |
28,6 |
1 |
11,1 |
11,30 |
Suma |
- |
- |
49 |
7,5 |
179,9 |
D = 179,9 / 49
D = 3,66
Procentowa stopa bezrobocia w poszczególnych województwach Polski średnio różni się od średniej arytmetycznej o 3,66%
MIARY ASYMETRII
Miary asymetrii (zwane też miarami skośności) służą do badania kierunku zróżnicowania wartości zmiennej.
Moment trzeci centralny m3 to średnia arytmetyczna z odchyleń poszczególnych wartości zmiennej od średniej arytmetycznej podniesionych do potęgi trzeciej.
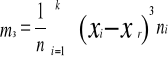
Tabela nr 6. Szereg rozdzielczy wielostopniowy z wartościami niezbędnymi do wyznaczenia momentu trzeciego centralnego.
Numer klasy |
Stopa bezrobocia w Polsce |
Środki przedziałów xi |
Liczba województw ni |
xi-xśr |
(xi-xśr)3ni |
|
<xi0 - xi1) |
|
|
|
|
1. |
6,5 - 9,9 |
8,2 |
3 |
-9,1 |
-2260,71 |
2. |
9,9 - 13,3 |
11,6 |
7 |
-5,7 |
-1296,35 |
3. |
13,3 - 16,7 |
15 |
10 |
-2,3 |
-121,67 |
4. |
16,7 - 20,1 |
18,4 |
18 |
1,1 |
23,96 |
5. |
20,1 - 23,5 |
21,8 |
6 |
4,5 |
546,75 |
6. |
23,5 - 26,9 |
25,2 |
4 |
7,9 |
1972,16 |
7. |
26,9 - 30,3 |
28,6 |
1 |
11,3 |
1442,9 |
Suma |
- |
- |
49 |
7,5 |
307,03 |
m3 = 307,3/ 49
m3 = 6,27
Procentowa stopa bezrobocia w poszczególnych województwach w Polsce charakteryzuje się asymetrią prawostronną, gdyż m3 > 0
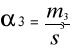
Moment trzeci względny α3 to iloraz wartości momentu trzeciego centralnego m3 przez sześcian odchylenia standardowego s3. Informuje zarówno o kierunku jak i sile asymetrii.
α3 = 6,27 / 99,2
α3 = 0,063
Rozkład procentowy stopy bezrobocia w poszczególnych województwach charakteryzuje się asymetrią dodatnią (prawostronną), gdyż α3 zawiera się w przedziale (0;2).
![]()
MIARY KONCENTRACJI
Miary koncentracji służą do badania stopnia nierównomierności rozkładu ogólnej sumy wartości zmiennej pomiędzy poszczególne jednostki zbiorowości lub do analizy skupienia poszczególnych jednostek wokół średniej.
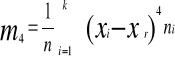
Moment czwarty centralny m4 to miara natężenia koncentracji (skupienia) poszczególnych obserwacji wokół średniej.
Tabela nr 7. Szereg rozdzielczy wielostopniowy z wartościami niezbędnymi do wyznaczenia momentu czwartego centralnego.
Numer klasy |
Stopa bezrobocia w % |
Środki przedziałów xi |
Liczba województw ni |
xi-xśr |
(xi-xśr)4ni |
|
<xi0 - xi1) |
|
|
|
|
1. |
6,5 - 9,9 |
8,2 |
3 |
-9,1 |
20572,49 |
2. |
9,9 - 13,3 |
11,6 |
7 |
-5,7 |
7389,20 |
3. |
13,3 - 16,7 |
15 |
10 |
-2,3 |
279,84 |
4. |
16,7 - 20,1 |
18,4 |
18 |
1,1 |
26,35 |
5. |
20,1 - 23,5 |
21,8 |
6 |
4,5 |
2460,38 |
6. |
23,5 - 26,9 |
25,2 |
4 |
7,9 |
15580,03 |
7. |
26,9 - 30,3 |
28,6 |
1 |
11,3 |
16304,74 |
Suma |
- |
- |
49 |
7,7 |
62613,03 |
m4 = 62613,03 / 49
m4 = 1277,8169
Moment czwarty względny α4 to miara informująca o wysmukłości krzywej liczebności, co sygnalizuje, że warianty zmiennej mają tendencję do skupiania się wokół średniej. Małe wartości α4 oznaczają rozkład spłaszczony, duże zaś wysmukły.
α4 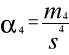
= 1277,8169 / 459,5407
α4 ≈ 2,8
Krzywa jest spłaszczona, ponieważ α4 <3. Oznacza to, że w typowym obszarze zmienności znajduje się mniej niż 68% obserwacji.
Współczynnik koncentracji Pearsona K to współczynnik przyjmujący wartości z przedziału <0 , 1>.
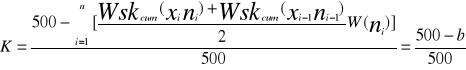
gdzie:
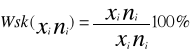
![]()
Tabela nr 8. Szereg rozdzielczy wielostopniowy z wartościami niezbędnymi do wyznaczenia współczynnika koncentracji Pearsona.
Stopa bezrobocia w % |
Środki przedziałów xi |
Liczba województw ni |
Iloczyn xini |
W ( ni) |
W (xini) |
Wsk (ni) |
Wsk(xini) |
b |
<xi0 - xi1) |
|
|
|
|
|
|
|
|
6,5 - 9,9 |
8,2 |
3 |
24,6 |
6,12 |
2,90 |
6,12 |
2,90 |
8,89 |
9,9 - 13,3 |
11,6 |
7 |
81,2 |
14,29 |
9,58 |
20,41 |
12,49 |
109,94 |
13,3 - 16,7 |
15 |
10 |
150 |
20,41 |
17,71 |
40,82 |
30,19 |
435,53 |
16,7 - 20,1 |
18,4 |
18 |
331,2 |
36,73 |
39,09 |
77,55 |
69,29 |
1827,20 |
20,1 - 23,5 |
21,8 |
6 |
130,8 |
12,24 |
15,44 |
89,80 |
84,73 |
942,94 |
23,5 - 26,9 |
25,2 |
4 |
100,8 |
8,16 |
11,90 |
97,96 |
96,62 |
740,21 |
26,9 - 30,3 |
28,6 |
1 |
28,6 |
2,04 |
3,38 |
100,00 |
100,00 |
200,64 |
Razem |
- |
49 |
847,2 |
100,00 |
100,00 |
- |
- |
4265,34 |
K = (5000 - 4265,34) / 5000
K = 0,147
Koncentracja procentowego udziału lokatorów zalegających ze spłacaniem kredytu mieszkaniowego w poszczególnych województwach nie jest silna.
Wykres nr 3. Krzywa Lorenza.
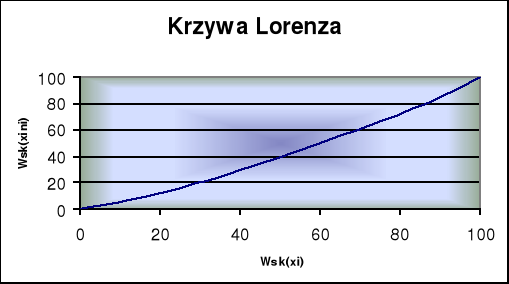
Krzywa Lorenza znajduje się blisko punktu linii równomiernego podziału. Potwierdza to wnioski wynikające z obliczonego współczynnika Pearsona, że stopa bezrobocia w poszczególnych województwach Polski nie jest silna.
Analizując strukturę procentową stopę bezrobocia w poszczególnych województwach Polski w 1994 roku zauważono, że przeciętna stopa bezrobocia wynosi 17,3 %, przy czym wartości w poszczególnych województwach odbiegają od tej wartości średnio o 4,63% Ich rozkład charakteryzuje się asymetrią dodatnią (prawostronną). Dwie trzecie badanej cechy mieści się w przedziale od 12,67% do 921,93%. Na podstawie wartości współczynnika koncentracji Pearsona stwierdzono, że koncentracja stopy bezrobocia w poszczególnych województwach Polski w 1994 roku nie jest silna.
2
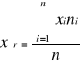
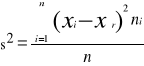
![]()
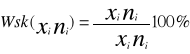
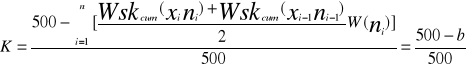
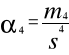
![]()
![]()
![]()
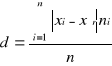
![]()
![]()
Wyszukiwarka