POLITECHNIKA LUBELSKA |
Laboratorium elektrotechniki |
|||
W Lublinie |
Ćwiczenie nr 6 |
|||
Nazwisko Pietrzyk |
Imię Darek |
Semestr 3 |
Grupa 3.5 |
Rok akad. 1996/97 |
Temat ćwiczenia Obwody nieliniowe zawierające prostownik |
Data wyk. 96XI20 |
Ocena |
||
Cel ćwiczenia
a. Badanie układów z prostownikami niesterowanymi.
rys. Układ pomiarowy
W1 - wyłącznik filtru wygładzania
W2 - wyłącznik obciążenia
Lp. |
Układ |
U'1 |
I'1 |
P |
U'2 |
U''2 |
I'2 |
I''2 |
R |
Pu |
|
|
V |
A |
W |
V |
V |
A |
A |
Ω |
W |
|
Układ prostownika jedno połówkowego |
|||||||||
1 |
z obciąż. z wygładzaniem |
85 |
0,8 |
38 |
104 |
104 |
0,33 |
0,33 |
330 |
35,9 |
2 |
z obciąż. bez wygładzania |
214 |
0,5 |
74 |
132 |
96 |
0,47 |
0,30 |
330 |
29,7 |
3 |
bez obciąż z wygładzaniem |
200 |
0 |
3 |
140 |
92 |
0 |
0 |
330 |
----- |
4 |
bez obciąż bez wygładzaniem |
200 |
0,19 |
14 |
280 |
280 |
0 |
0 |
330 |
----- |
|
Układ prostownika dwu połówkowego |
|||||||||
5 |
z obciąż. z wygładzaniem |
90 |
0,8 |
47 |
116 |
120 |
0,36 |
0,36 |
330 |
42,7 |
6 |
z obciąż. bez wygładzania |
152 |
0,5 |
76 |
152 |
136 |
0,47 |
0,43 |
330 |
61,1 |
7 |
bez obciąż z wygładzaniem |
200 |
0 |
6 |
200 |
162 |
0 |
0 |
330 |
----- |
8 |
bez obciąż bez wygładzania |
200 |
0,15 |
14 |
280 |
280 |
0 |
0 |
330 |
----- |
1. Prostownik półfalowy, z obciążeniem i z wygładzaniem
wyznaczanie współczynników szeregu Fouriera, stosując metodę Perry'ego
ak |
bk |
Uk |
|
-12,234 |
23,77822 |
26,74089 |
U=106 |
-9,40703 |
7,219112 |
11,85782 |
U=156 |
-5,42959 |
2,110339 |
5,825292 |
U=104 |
-4,09041 |
0,475599 |
4,117962 |
k=1,02 |
-1,94009 |
0,063054 |
1,941118 |
s=1,443 |
-2,00802 |
0,179827 |
2,01606 |
z=2,42 |
-1,32389 |
0,803394 |
1,548585 |
|
Przykłady obliczeń b3
ζ= 16
b3= 2/16 ( 1,7*cos(3*1*2π/16)+ 2*cos(3*2*2π/16)+ 2,1*cos(3*3*2π/16) +2,65*cos(3*4*2π/16) +2*cos(3*5*2π/16)+ 1,93*cos(3*6*2π/16)+ 1,85*cos(3*7*2π/16)+ 1,75*cos(3*8*2π/16)+ 1,7*cos(3*9*2π/16)+ 1,65*cos(3*10*2π/16)+ 1,55*cos(3*11*2π/16)+ 1,5*cos(3*12*2π/16)+ 1,4*cos(3*13*2π/16)+ 1,35*cos(3*14*2π/16)+ 1,25*cos(3*15*2π/16) + 1,2*cos(3*16*2π/16) ) = 0,125*(0,65056-1,4142-1,9401+1,84776+1,3647-0,70796-1,75-0,65056 +1,1667 +1,4320 -1,2934 -0,9546 +0,4783+1,2) =0,076548
2 Prostownik półfalowy z obciążeniem, bez wygładzania.
Wyznaczanie wsp. szeregu Fouriera metodą liczbową Perry'ego.
ak |
bk |
Uk |
|
4,93E-05 |
150,9364 |
150,9364 |
U=132 |
-44,6328 |
2,92E-05 |
44,63281 |
Um=264 |
2,66E-05 |
27,1382 |
27,1382 |
Us=96 |
-24,645 |
3,22E-05 |
24,64503 |
k=1,375 |
1,9E-05 |
11,62463 |
11,62463 |
s=2 |
-21,3973 |
4,2E-05 |
21,39725 |
z=1,064 |
7,69E-06 |
3,362803 |
3,362803 |
|
Prostownik półfalowy, bez obciążenia i bez wygładzania.
Przebieg napięć pokazywanych przez oscyloskop w tym układzie nie różni się ( wzrokowo różnice są nie zauważalne) od przebiegów napięcia w układzie 2 tzn. z obciążeniem i bez wygładzania. Dlatego też wszystkie współczynniki są takie same i aktualna jest tabela z układu 2.
Prostownik półfalowy, bez obciążenia i z wygładzaniem.
Wyznaczanie wsp. szeregu Fouriera metodą liczbową Perry'ego.
ak |
bk |
Uk |
|
-6,7974 |
5,463614 |
8,720992 |
U=280 |
-3,84458 |
-1,07715 |
3,992628 |
Um=280 |
-0,27408 |
-1,91977 |
1,939232 |
Us=285 |
-0,25059 |
-0,83509 |
0,871874 |
k=1 |
0,122247 |
-0,25329 |
0,281243 |
s=1,02 |
0,17042 |
-0,57624 |
0,600911 |
|
0,268912 |
-0,218 |
0,346173 |
|
5 Prostownik całofalowy z obciążeniem i z wygładzaniem.
Wyznaczanie wsp. szeregu Fouriera metodą liczbową Perry'ego.
ak |
bk |
Uk |
|
-8,2E-05 |
-5,3E-06 |
8,26E-05 |
U=120 |
-106,767 |
10,83277 |
107,3147 |
Um=133 |
5,55E-05 |
-3E-05 |
6,3E-05 |
Us=116 |
94,47747 |
1,657216 |
94,492 |
k=1.034 |
-0,00019 |
-4,6E-05 |
0,000196 |
s=1,11 |
-102,078 |
0,887993 |
102,0823 |
z=2,22 |
0,000216 |
-6,4E-05 |
0,000226 |
|
Prostownik całofalowy z obciążeniem i bez wygładzania.
Wyznaczanie wsp. szeregu Fouriera metodą liczbową Perry'ego.
ak |
bk |
Uk |
|
-4,9E-05 |
3,2E-11 |
4,89E-05 |
U=152 |
-47,4488 |
6,2E-05 |
47,4488 |
Um=215 |
-2,3E-05 |
4,48E-11 |
2,28E-05 |
Us=136 |
-23,868 |
6,24E-05 |
23,86802 |
k=1,11 |
-1,5E-05 |
4,78E-11 |
1,46E-05 |
s=1,41 |
-18,8513 |
7,39E-05 |
18,85125 |
z=1,064 |
-6,5E-06 |
2,95E-11 |
6,45E-06 |
|
Prostownik całofalowy, bez obciążenia i bez wygładzania.
Przebieg napięć pokazywanych przez oscyloskop w tym układzie różni się od przebiegu napięć w układzie 6 tylko nieco zwiększonym napięciem, kształt natomiast pozostał taki sam w związku z czym współczynniki kształtu, amplitudy itp. mają takie same wartości.
Prostownik całofalowy, z obciążeniem i bez wygładzania.
Wykres napięcia pokazywany przez oscyloskop w tym układzie jest linią prostą, ( drobne odchyłki były już nie do odczytania ) w związku z tym wszystkie współczynniki rozwinięcia w szereg Fouriera są zerami, oraz
U = Us = Um = 280V
k = s = 1
Badanie układów z prostownikami sterowanymi.
Rys. Układ pomiarowy prostownika sterowanego.
Tabela pomiarów.
Układ |
U'1 |
I'1 |
P |
U'2 |
U''2 |
I'2 |
I''2 |
θ |
R |
PU |
|
V |
A |
W |
V |
V |
A |
A |
Rad |
Ω |
W |
1 |
220 |
0.5 |
80 |
152 |
186 |
0.5 |
0.31 |
0.3 |
330 |
31.7 |
2 |
220 |
0.49 |
78 |
150 |
184 |
0.495 |
0.305 |
0.62 |
330 |
30.7 |
3 |
220 |
0.49 |
76 |
148 |
176 |
0.49 |
0.29 |
0.78 |
330 |
27.7 |
4 |
220 |
0.46 |
68 |
144 |
160 |
0.465 |
0.26 |
0.94 |
330 |
22.3 |
5 |
220 |
0.44 |
62 |
136 |
144 |
0.45 |
0.24 |
1.1 |
330 |
19 |
6 |
220 |
0.41 |
54 |
128 |
132 |
0.42 |
0.22 |
1.25 |
330 |
15.9 |
7 |
220 |
0.36 |
42 |
112 |
104 |
0.37 |
0.17 |
1.57 |
330 |
9.53 |
8 |
220 |
0.33 |
32 |
104 |
92 |
0.34 |
0.15 |
1.73 |
330 |
7.42 |
9 |
220 |
0.28 |
27 |
90 |
76 |
0.29 |
0.12 |
1.88 |
330 |
4.75 |
10 |
220 |
0.2 |
13 |
64 |
44 |
0.2 |
0.075 |
2.19 |
330 |
1.856 |
11 |
220 |
0.17 |
9 |
52 |
36 |
0.17 |
0.06 |
2.35 |
330 |
1.188 |
Wyznaczanie wsp. szeregu Fouriera metodą liczbową Perry'ego.
ak |
bk |
Uk |
|
-22,865975 |
125,9608 |
128,0194 |
U=143,3 |
-37,42601 |
-17,5009 |
41,3157 |
Um=300 |
-9,4713616 |
37,29283 |
38,47678 |
Us=89 |
-61,125033 |
-24,7499 |
65,94565 |
k=1,61 |
9,47136625 |
-46,9543 |
47,90002 |
s=2,09 |
29,9259389 |
-17,5009 |
34,66763 |
|
22,8660958 |
26,71359 |
35,16353 |
|
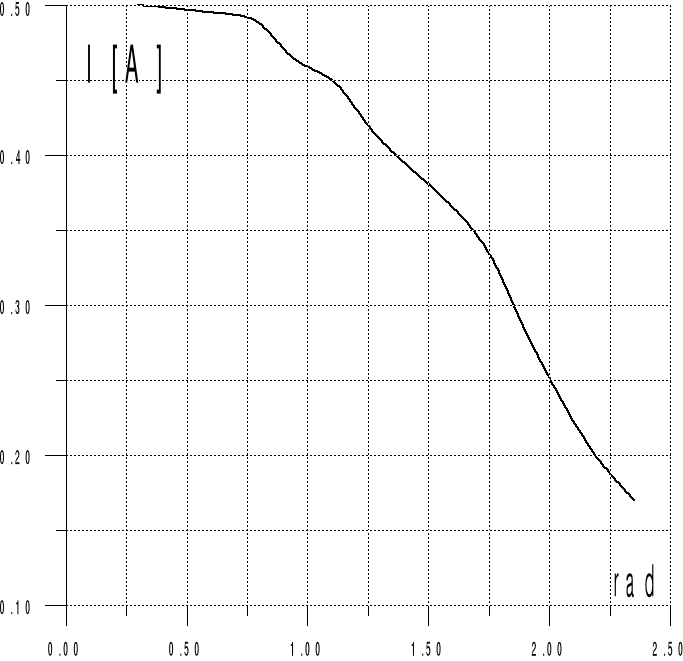
Rys. Wykres przedstawiający zależność prądu w funkcji kąta zapłonu
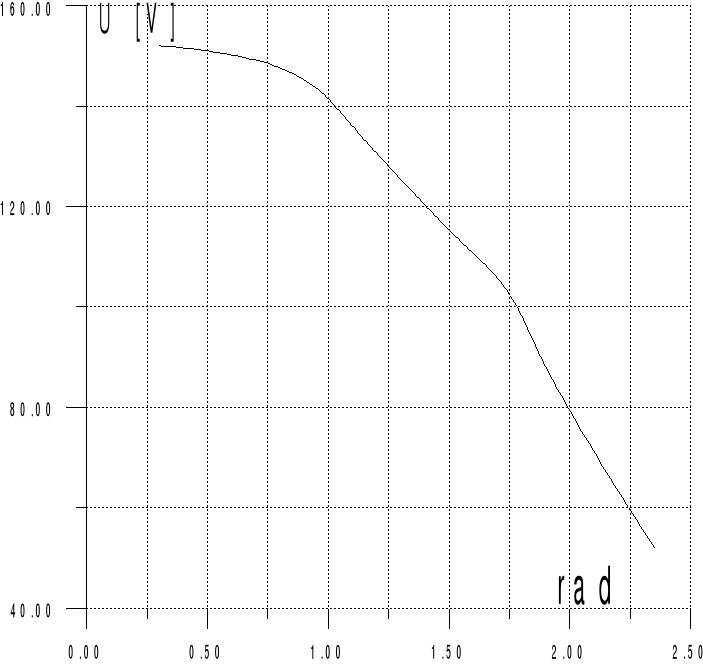
Rys. Wykres przedstawiający zależność napięcia w funkcji kąta zapłonu
Wnioski
Stosując metodę Perry'ego można wyznaczyć współczynniki szeregu Fouriera funkcji mając jedynie jej wykres, bez konieczności aproksymacji otrzymanej funkcji. Umożliwia to rozkład na szereg Fouriera dowolnych napięć czy prądów przerysowanych np. z ekranu oscyloskopu. Jednak aby otrzymać dokładne wyniki obszar pod krzywą na długości jednego pełnego okresu należy podzielić na jak najwięcej części. Wzrostowi liczby podziałów towarzyszy jednak duży wzrost obliczeń jakie trzeba przeprowadzić aby otrzymać wynik. Obliczenia przeprowadzane ręcznie przy użyciu kalkulatora są bardzo żmudne i czasochłonne, a przez to skazane na liczne pomyłki. Bardzo pomocny jest tutaj komputer który wydatnie przyśpiesz obliczenia. Większość obliczeń przeprowadziłem przy pomocy arkusza kalkulacyjnego, który znacznie przyśpieszył obliczenia ( i tak długie).
Dla prostownika półfalowego największy udział z harmonicznych ma pierwsza harmoniczna, kolejne są coraz mniejsze. Dla układu prostownika całofalowego widoczny jest udział głównie harmonicznych parzystych (2,4,6 itd.). Udział harmonicznych nieparzystych jest tutaj znikomy.
Dla prostownika sterowanego można zauważyć duży udział wyższych harmonicznych w porównaniu ze zwykłymi prostownikami. 8 harmoniczna stanowi jeszcze około 30% wartości pierwszej, świadczy to o tym że prostowniki sterowane wprowadzają duże zakłócenia w postaci wyższych harmonicznych.
Przy badaniu układu z prostownikiem sterowanym, kąt zapłonu otrzymywany był na podstawie obserwacji wykresu napięcia na oscyloskopie, przez co jego wartości są obarczone dużym błędem.
Wyszukiwarka