Utwórzmy nowy ciąg liczbowy {Sn}, którego n-ty wyraz wyraża się sumą: Sn=![]()
.
SZEREGI LICZBOWE I FUNKCYJNE
Niech a1, a2,..., an,... (wyrazy szeregu) będzie dowolnym nieskończonym ciągiem liczbowym liczb rzeczywistych zbieżnym lub rozbieżnym.
Utwórzmy nowy ciąg liczbowy {Sn}, którego n-ty wyraz wyraża się sumą: Sn=![]()
.
Definicja szeregu liczbowego:
Szeregiem liczbowym nazywamy ciąg {Sn}, gdzie Sn=![]()
i oznaczamy go przez: ![]()
(1).
Jeżeli mamy szereg (1), to ciąg postaci {Sn}, gdzie Sn=![]()
nazywamy ciągiem sum częściowych dla szeregu (1).
Definicja zbieżności szeregu liczbowego:
Mówimy, że szereg (1) jest zbieżny, jeżeli ciąg jego sum częściowych {Sn}, gdzie Sn=![]()
jest zbieżny do granicy właściwej. W przeciwnym przypadku mówimy, że szereg jest rozbieżny.
Zapis nieformalny: Sn=S lub ![]()
S - suma szeregu
![]()
![]()
- szereg zbieżny
![]()
- szereg rozbieżny
Przykład:
rozważmy szereg ![]()
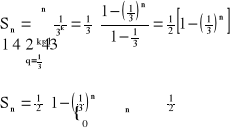
![]()
- szereg zbieżny
rozważmy szereg ![]()
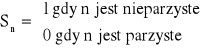
{Sn} nie jest zbieżny czyli ![]()
nie jest zbieżny.
Twierdzenie: warunek konieczny zbieżności szeregu liczbowego:
Jeżeli szereg ![]()
jest zbieżny, to ciąg jego wyrazów jest zbieżny do zera, czyli:
![]()
Dowód: Sn→S![]()
an = Sn - Sn-1 = a1+a2+...+an - (a1+a2+an-1) = an
Sn-1→S![]()
an = Sn - Sn-1 ![]()
S - S = 0
Przykład:
![]()
an=![]()
- niespełniony warunek konieczny zbieżności ciągu, szereg rozbieżny
![]()
- tzw. szereg harmoniczny - rozbieżny, chociaż spełnia warunek konieczny zbieżności
an=![]()
Definicja szeregu geometrycznego:
Szeregiem geometrycznym nazywamy szereg postaci:
![]()
,
w którym wyraz początkowy p i iloraz q są liczbami dowolnymi.
Jeżeli a=0, to szereg jest zbieżny i ma sumę równą 0.
Jeżeli a≠0 i |q| > 1, to ciąg wyrazów nie dąży do zera o szereg jest rozbieżny.
Jeżeli |q| < 1, to szereg jest rozbieżny, ponieważ nie spełnia on warunku koniecznego zbieżności:
|an| = |aqn-1| > |a |> 0.
Otrzymujemy:
![]()
Definicja szeregu harmonicznego:
Szeregiem harmonicznym nazywamy szereg, którego wyrazy są odwrotnościami liczby naturalnych:
![]()
Szereg harmoniczny jest rozbieżny, a ciąg jego sum częściowych rośnie do +∞.
Dowód: Wykażmy, że ciąg sum częściowych jest nieograniczony.
Niech A będzie dowolną liczbą.
Grupując wyrazy szeregu: ![]()
stwierdzamy, że każda grupa ma wartość większą od 0,9.
Biorąc dostatecznie wiele takich grup, otrzymamy sumę częściową większą od A.
Szereg harmoniczny rzędu r>1 jest zbieżny.
Dowód: Ciąg sum częściowych {Sn} jest rosnący; wystarczy wykazać ze jest on ograniczony. Grupując wyrazy szeregu: ![]()
stwierdzamy, że pierwsza grupa obejmuje 9 wyrazów, wśród których największym jest 1, więc wartość tej grupy nie przekracza 9. Druga grupa zawiera 90 wyrazów, z nich największym jest ![]()
, więc wartość tej grupy nie przekracza ![]()
. Wartość trzeciej grupy nie przekracza ![]()
. Uzyskane w ten sposób ograniczenia górne kolejnych grup są wyrazami szeregu geometrycznego o ilorazie ![]()
<1. Dla dowolnego n otrzymujemy: 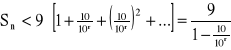
, co oznacza, że ciąg {Sn} jest ograniczony.
Szereg harmoniczny rzędu r<1 jest rozbieżny.
Dowód: Ponieważ r<1, więc ![]()
. Wyrazy rozważanego szeregu są niemniejsze od wyrazów szeregu ![]()
, zatem ciąg sum częściowych rozważanego szeregu jest nieograniczony.
Przykład: Szereg harmoniczny rzędu 2 jest zbieżny i można udowodnić, że jest:
![]()
Szereg harmoniczny rzędu ![]()
jest rozbieżny:
![]()
Obydwa powyższe szeregi spełniają warunek: ![]()
.
Twierdzenie:
Jeżeli szereg ![]()
jest zbieżny i szereg ![]()
jest zbieżny to:
![]()
Twierdzenie:
Jeżeli szereg ![]()
jest zbieżny, to:
![]()
, c![]()
R
§1. SZEREGI O WYRAZACH NIEUJEMNYCH
Twierdzenie:
Jeżeli ciąg sum częściowych szeregu o wyrazach nieujemnych jest ograniczony z góry, to szereg ten jest zbieżny.
Dowód: Załóżmy, że ciąg an jest rosnący o ograniczony. Niech Z oznacza zbiór wartości wyrazów tego ciągu. Jest to zbiór ograniczony, więc istnieje kres górny tego zbioru i oznaczamy go literą g. Mamy: g=supZ. Wykażmy teraz, że g=![]()
.
Z własności kresu górnego wynika, że:
an<g, dla n![]()
N
dla każdego ε>0 istnieje wyraz aδ spełniający nierówność: g - ε < aδ < g.
Ponieważ ciąg an jest rosnący, więc dla n>δ jest: g - ε < aδ <an < g, czyli an![]()
U(g,ε) dla n>δ; oznacza to, że g=![]()
.
Zgodnie z 1) żaden wyraz ciągu nie jest większy od granicy; nie jest równy granicy, gdyż wtedy następny wyraz musiałby być większy od granicy. Zatem: ![]()
.
Twierdzenie: kryterium porównawcze:
Jeżeli wyrazy szeregu (1): ![]()
i szeregu (2): ![]()
są nieujemne i istnieje liczba T![]()
N, że dla każdego n>T: an < bn, to:
ze zbieżności szeregu (2) wynika zbieżność szeregu (1)
z rozbieżności szeregu (1) wynika rozbieżność szeregu (2)
Przykład:
![]()
Szacujemy ![]()
z dołu przez ![]()
, dla n > 1: ![]()
<![]()
![]()
- rozbieżny jako szereg harmoniczny
Na podstawie punktu 2) w/w twierdzenia szereg ![]()
jest rozbieżny.
![]()
- szereg o wyrazach nieujemnych
Podejrzewając, że jest on zbieżny, szacujemy go z góry: ![]()
<![]()
, dla n![]()
N
![]()
- zbieżny, co wcześniej sprawdziliśmy
Z punktu 1) w/w twierdzenia wynika, że ![]()
jest zbieżny.
Często, jako szereg porównawczy, wykorzystuje się tzw. szereg Dirichleta: ![]()
dla α < 1 - rozbieżny
dla α > 1 - zbieżny
Twierdzenie: kryterium d'Alemberta (ilorazowe):
Jeżeli istnieje granica ![]()
(właściwa lub niewłaściwa), to szereg o wyrazach dodatnich ![]()
jest zbieżny, gdy g < 1, a rozbieżny, gdy g > 1. Gdy g = 1, to kryterium to nie rozstrzyga zbieżności szeregu!
Przykład: Zbadać zbieżność szeregu: ![]()
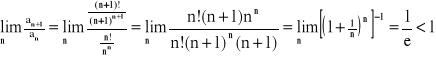
- szereg zbieżny
Twierdzenie: kryterium Cauchy'ego (pierwiastkowe):
Jeżeli istnieje granica ![]()
(właściwa lub niewłaściwa), to szereg o wyrazach nieujemnych ![]()
jest zbieżny, gdy g < 1, a rozbieżny, gdy g > 1. Gdy g = 1, to kryterium to nie rozstrzyga zbieżności szeregu!
Przykład: Zbadać zbieżność szeregu: ![]()
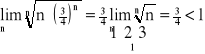
- szereg zbieżny
Twierdzenie: kryterium całkowe:
Niech funkcja f(x) będzie ciągła, dodatnia i malejąca w przedziale <T,+∞), gdzie T jest pewną ustaloną liczbą naturalną i dla każdego n![]()
N takiego, że n > T f(n)=an, to szereg o wyrazach nieujemnych![]()
jest zbieżny (rozbieżny) wtedy i tylko wtedy, gdy zbieżna (rozbieżna) jest całka:
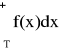
Przykład: Rozważmy szereg Dirichleta: ![]()
Zauważmy, że dla α < 0 szereg ten jest rozbieżny, ponieważ nie spełnia warunku koniecznego zbieżności szeregu.
Rozpatrzmy α > 0:
![]()
, w przedziale <1,+∞) funkcja f(x) jest ciągła, dodatnia i malejąca, bo: ![]()
, dla x![]()
<1,+∞).
![]()
α ≠ 1: 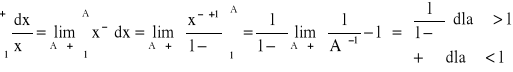
α = 1: 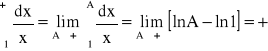
Na podstawie kryterium całkowego szereg Dirichleta ![]()
jest rozbieżny dla α<1 i zbieżny dla α>1.
§2. SZEREGI O WYRAZACH NIEUJEMNYCH
Definicja szeregu przemiennego:
Szereg o wyrazach dowolnych w postaci ![]()
, gdzie:
an > 0, dla n=1,2,...
an+1 < an, dla n=1,2,...
![]()
nazywamy szeregiem przemiennym.
Szereg postaci ![]()
nazywamy szeregiem anharmonicznym i jest on przykładem szeregu przemiennego, ponieważ: an=![]()
>0, an+1 < an, ![]()
Twierdzenie: kryterium Leibniza:
Każdy szereg przemienny jest zbieżny.
Definicja bezwzględnej zbieżności szeregu:
Mówimy, że szereg ![]()
o wyrazach dowolnych jest bezwzględnie zbieżny, jeżeli zbieżny jest szereg ![]()
.
Definicja warunkowej zbieżności szeregu:
Mówimy, że szereg ![]()
o wyrazach dowolnych jest warunkowo zbieżny, jeżeli rozbieżny jest szereg ![]()
, a szereg ![]()
jest zbieżny.
Twierdzenie:
Każdy szereg bezwzględnie zbieżny jest zbieżny!!!
Przykład: Zbadać zbieżność szeregu o wyrazach dowolnych:
![]()
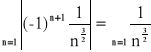
- jest zbieżny jako szereg Dirichleta, α = ![]()
>1.
Jest on bezwzględnie zbieżny.
![]()
- jest zbieżny i przemienny jako szereg harmoniczny
![]()
- rozbieżny jako szereg harmoniczny,
czyli szereg ![]()
jest zbieżny warunkowo.
§3. CIĄG FUNKCYJNY
Definicja ciągu funkcyjnego:
Ciąg funkcyjny to przyporządkowanie każdej liczbie naturalnej jednej funkcji.
{fn}≡f1,f2,...,fn,... fk: X→R, X![]()
R
{fn(x)}
Definicja zbieżności (zwykłej) ciągu funkcyjnego:
Mówimy, że ciąg funkcyjny {fn} jest zbieżny na zbiorze X do funkcji f, co zapisujemy:
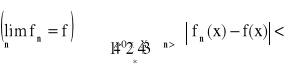
[dla każdego ε>0 i dla każdego x![]()
X istnieje takie δ, że dla każdego n>δ
prawdziwa jest nierówność: |fn(x)-f(x)|<ε]
* - δ zależne od ε i od x
Definicja jednostajnej zbieżności ciągu funkcyjnego:
Mówimy, że ciąg funkcyjny {fn} jest jednostajnie zbieżny na zbiorze X do funkcji granicznej f, co zapisujemy:
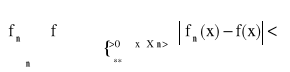
** - δ zależne tylko od ε
Uwaga: Z jednostajnej zbieżności ciągu funkcyjnego wynika zbieżność zwykła!!!
Twierdzenie o ciągłości funkcji granicznej:
Jeżeli wyrazy ciągu {fn} (tzw. funkcje fn) są ciągłe na zbiorze X i ciąg {fn} jest jednostajnie zbieżny do funkcji f na zbiorze X 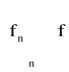
to funkcja graniczna f jest ciągła na zbiorze X.
Przykład: {xn}, x![]()
<0,1>
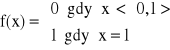
wykres funkcji granicznej
Funkcja graniczna nie jest ciągła pomimo tego, że funkcje fn są ciągłe w zbiorze X: <0,1>
§4. SZEREGI FUNKCYJNE
Niech będzie dany ciąg funkcyjny {fn}≡f1,f2,...,fn,... , fk: X→R, n=1,2,... . Może on być zbieżny lub rozbieżny.
Tworzymy nowy ciąg funkcyjny {Sn}, gdzie Sn=![]()
.
Definicja szeregu funkcyjnego:
Szeregiem funkcyjnym nazywamy ciąg funkcyjny {Sn}, Sn=![]()
i oznaczamy go przez:
![]()
Jeżeli mamy szereg ![]()
, to o ciągu {Sn}, Sn=![]()
mówimy, że jest ciągiem sum częściowych w/w szeregu.
Definicja zbieżności (zwykłej) szeregu funkcyjnego:
Mówimy, że szereg ![]()
jest zbieżny w zbiorze X do funkcji S, jeżeli ciąg jego sum częściowych {Sn}, Sn=![]()
jest zbieżny do S w zbiorze X (Sn![]()
S)
![]()
Definicja jednostajnej zbieżności szeregu funkcyjnego:
Mówimy, że szereg funkcyjny ![]()
jest jednostajnie zbieżny w zbiorze X i jego suma wynosi S, jeżeli ciąg jego sum częściowych {Sn} jest zbieżny jednostajnie do S w zbiorze X (Sn![]()
S)
Definicja bezwzględnej zbieżności szeregu funkcyjnego:
Mówimy, że szereg funkcyjny ![]()
jest bezwzględnie zbieżny w zbiorze X, jeżeli zbieżny jest szereg ![]()
, x![]()
X.
Twierdzenie: kryterium Weiestrassa:
Jeżeli istnieje liczba naturalna N, że dla każdego n>N i dla każdego x![]()
X spełniona jest nierówność |fn(x)|<an ![]()
i jeżeli szereg liczbowy ![]()
jest zbieżny, to szereg funkcyjny ![]()
jest bezwzględnie i jednostajnie zbieżny w zbiorze X.
![]()
- jest to majoranta liczbowa szeregu funkcyjnego ![]()
, która szacuje go z góry.
Przykład: Rozważmy szereg ![]()
i zbadajmy jego zbieżność.
Skorzystajmy z kryterium Weiestrassa:
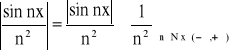
![]()
- jest zbieżny, jako szereg Dirichleta, α=2
Na podstawie kryt. Weiestrassa szereg funkcyjny ![]()
jest bezwzględnie i jednostajnie zbieżny.
Twierdzenie o całkowaniu szeregu funkcyjnego:
Jeżeli wyrazy szeregu ![]()
są funkcjami ciągłymi w przedziale <a,b> i szereg ten jest jednostajnie zbieżny w przedziale <a,b>, to spełniona jest równość:
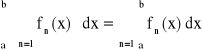
Twierdzenie o różniczkowaniu szeregu funkcyjnego:
Jeżeli wyrazy szeregu ![]()
posiadają ciągłe pochodne (fn' - są ciągłe, I rzędu) oraz szereg ![]()
jest zbieżny i szereg ![]()
jest jednostajnie zbieżny w przedziale <a,b>, to spełniona jest równość:
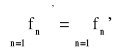
w <a,b>
Przykład: Rozważmy szereg ![]()
.
![]()
- ciągła dla x![]()
(-∞,+∞)
![]()
![]()
- jest zbieżny, jako szereg Dirichleta, α=3
Na podstawie kryterium Weiestrassa szereg ![]()
jest bezwzględnie i jednostajnie zbieżny.
Zbadajmy zatem, czy szereg ![]()
jest zbieżny.
![]()
![]()
- jest zbieżny, jako szereg Dirichleta, α=2
Na podstawie kryterium Weiestrassa szereg ![]()
jest bezwzględnie i jednostajnie zbieżny.
Z powyższych założeń wynika, że szereg ![]()
można różniczkować wyraz po wyrazie.
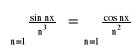
§5. SZEREGI POTĘGOWE
Definicja szeregu potęgowego:
Szereg funkcyjny postaci:
![]()
(1)
nazywamy szeregiem potęgowym, gdzie a0,a1,...![]()
R -są to współczynniki szeregu potęgowego, x0![]()
R.
Często szereg potęgowy wyraża się w następującej postaci (gdy x0=0)
![]()
(2)
Twierdzenie o zbieżności szeregu potęgowego:
Jeżeli szereg potęgowy (2) jest zbieżny w x0≠0, to jest on bezwzględnie zbieżny w przedziale
(-|x0|,|x0|) i jednostajnie zbieżny w każdym przedziale domkniętym zwartym w przedziale (-|x0|,|x0|), tj. w (-θ|x0|,θ|x0|), gdzie: 0<θ<1.
Oznaczmy przez Z zbiór wartości bezwzględnych wszystkich x![]()
X, dla których szereg (2) jest zbieżny.
Rozpatrzmy kres górny tego zbioru:
0 < supZ < +∞
Definicja promienia zbieżności:
Promieniem zbieżności R szeregu potęgowego (2) nazywamy kres górny bezwzględnych wartości x![]()
X, dla których szereg (2) jest zbieżny.
R = supZ
R = 0
0 < R < +∞
R = +∞
Twierdzenie:
Jeżeli granica: 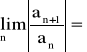
, to promień zbieżności jest równy:
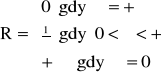
Przykład: Wyznaczyć przedział zbieżności szeregu potęgowego ![]()
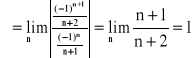
![]()
(-1,1) - przedział zbieżności; w nim szereg jest zbieżny, a poza nim rozbieżny. W punktach: -1 i 1
nie wiemy czy jest zbieżny czy rozbieżny.
x = -1
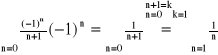
- jest to szereg harmoniczny, rozbieżny
x = 1
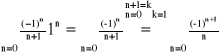
- jest to szereg anharmoniczny, zbieżny
Przedziałem zbieżności szeregu ![]()
jest przedział (-1,1>
Uwaga: Jeżeli: ![]()
, to: 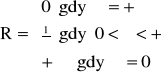
Przykład: Wyznaczyć przedział zbieżności szeregu ![]()
.
![]()
![]()
![]()
- przedział zbieżności; w nim szereg jest zbieżny, a poza nim rozbieżny. W punktach: -1 i 1
nie wiemy czy jest zbieżny czy rozbieżny.
x = ![]()
![]()
- szereg rozbieżny
x = ![]()
![]()
- szereg rozbieżny
Przedział pozostaje otwarty: ![]()
.
Twierdzenie o całkowaniu szeregu potęgowego:
Jeżeli x należy do przedziału zbieżności szeregu potęgowego (2), to prawdziwa jest równość:
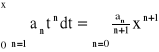
przy czym promień zbieżności otrzymanego szeregu jest taki sam jak szeregu wyjściowego.
Twierdzenie o różniczkowaniu szeregu potęgowego:
Jeżeli x należy do przedziału zbieżności szeregu potęgowego (2), to prawdziwa jest równość:
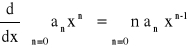
przy czym promień zbieżności otrzymanego szeregu jest taki sam jak szeregu wyjściowego.
§6. SZEREG TAYLORA
Twierdzenie:
Jeżeli funkcja f posiada wszystkie pochodne (jest klasy C∞) w otoczeniu Q punktu x0, to można napisać dla tej funkcji następujący wzór:
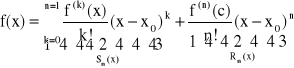
Rn(x) - reszta wzoru Taylora, c![]()
(x0,x) lub c![]()
(x,x0)
Jeżeli uda się dobrać takie otoczenie Q0 punktu x0 o promieniu δ i zajdzie zależność: ![]()
dla x![]()
Q0(x0,δ), to funkcja f(x) jest sumą następującego szeregu:
![]()
(1)
czyli spełniona jest równość:
f(x)=![]()
(2)
Szereg (1) nazywamy szeregiem Taylora funkcji f w otoczeniu Q0(x0,δ), a o równaniu (2) mówimy, że funkcja f(x) jest rozwijalna w szereg Taylora.
Jeżeli funkcja f posiada wszystkie pochodne (jest klasy C∞), to można dla niej napisać szereg Taylora, ale szereg ten nie musi być do niej zbieżny, tzn. że równość (2) nie musi być spełniona. Dopiero, jeśli w toczeniu Q0(x0,δ) zachodzi: ![]()
, to możemy stwierdzić, że szereg jest zbieżny do funkcji f, czyli równość (2) jest spełniona.
Jeżeli w szeregu (1) x0=0, czyli:
![]()
to taki szereg nazywamy szeregiem Maclaurina dla funkcji f.
Lemat o reszcie wzoru Taylora:
Jeżeli istnieje taka liczba naturalna N i istnieje liczba M, że dla każdego n>N spełniona jest nierówność: ![]()
, dla x![]()
Q0(x0,δ), to:
![]()
, dla x![]()
Q0(x0,δ)
Dowód:
Oszacujmy 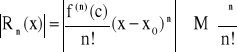
Łatwo sprawdzić, że z kryterium d'Alemberta szereg: ![]()
Z warunku koniecznego zbieżności szeregu wynika, że ![]()
Czyli:
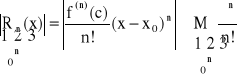
Przykład: Rozwinąć w szereg Maclaurina funkcję f(x)=ex.
![]()
f(x)=ex f(0)=1
f'(x)= ex f'(0)=1
f”(x)= ex f”(0)=1
![]()
![]()
f(n)(x)=ex
![]()
Rozważmy otoczenie Q0(0,δ)
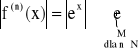
dla x![]()
Q0(0,δ)
![]()
, dla x![]()
Q0(0,δ)
Utwórzmy szereg Maclaurina:
![]()
(*) ![]()
, dla x![]()
Q0(0,δ)
Ze względu na dowolność doboru δ, x![]()
(-∞,+∞)
(*) Jeżeli przyjmiemy, że x=1, to:
![]()
- definicja liczby e
Jeżeli dla jakiejś funkcji f posiadającej wszystkie pochodne napiszemy, że funkcja ta jest sumą następującego szeregu potęgowego:
![]()
to szereg ten jest szeregiem Maclaurina i ![]()
.
Przykład: Rozwinąć w szereg Maclaurina funkcję f(x)=(1+x)α, α ![]()
R
f(x)=(1+x)α f(0)=1
f'(x)=α(1+x)α-1 f'(0)=1!![]()
f”(x)=α(α-1)(1+x)α-2 f”(0)=2!![]()
f”'(x)=α(α-1)(α-2)(1+x)α-3 f”'(0)=3!![]()
![]()
![]()
f(n)(x)= α(α-1)(α-2)∙...∙[α -(n-1)](1+x)α-n f(n)(c)=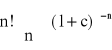
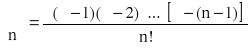
Rn(x)= 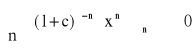
, jeżeli |x|<1
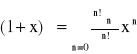
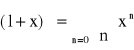
, |x|<1
§7. SZEREGI TRYGONOMETRYCZNE FOURIERA
Niech funkcja jednej zmiennej będzie całkowalna w przedziale <-l,l>. Dla tej funkcji można napisać szereg trygonometryczny Fouriera w postaci:
![]()
gdzie: 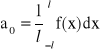
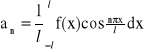
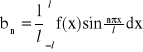
n = 1, 2, 3, ...
~ - odpowiada
Definicja funkcji przedziałami monotonicznej:
Mówimy, że funkcja f jest przedziałami monotoniczna w przedziale (a,b), jeżeli przedział (a,b) da się podzielić na skończoną liczbę przedziałów, w których funkcja ta jest monotoniczna.
Definicja punktów nieciągłości pierwszego i drugiego rodzaju:
Punkt x0 jest punktem nieciągłości I rodzaju funkcji f, jeżeli w tym punkcie istnieją właściwe granice jednostronne tej funkcji.
Punkt x0 jest punktem nieciągłości II rodzaju funkcji f, jeżeli co najmniej jedna z granic jednostronnych tej funkcji jest niewłaściwa.
Przykład:
1) ![]()
x0=0
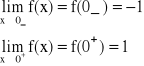
x0=0 - punkt nieciągłości I rodzaju
2) f(x) = tgx
x0=![]()
- punkt nieciągłości II rodzaju
Definicja warunków Dirichleta:
Mówimy, że funkcja f spełnia warunki Dirichleta w przedziale <a,b>, jeżeli
funkcja f jest przedziałami monotoniczna w (a,b)
funkcja f jest ciągła z wyjątkiem skończonej liczby punktów nieciągłości I rodzaju, przy czym w punkcie nieciągłości x0 zachodzi równość:
f(x0) = ![]()
w końcach przedziału <a,b> funkcja f przyjmuje postać:
f(a) = f(b) = 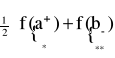
* - granica prawostronna
** - granica lewostronna
Twierdzenie Dirichleta:
Jeżeli funkcja f spełnia warunki Dirichleta w przedziale <-l,l>, to jest ona rozwijalna w szereg trygonometryczny Fouriera, czyli:
![]()
, dla x![]()
<-l,l>
gdzie: 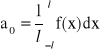
, 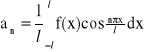
, 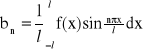
, n = 1, 2, 3, ...,
a ponadto, jeżeli funkcja f jest okresowa o okresie 2l, to powyższa równość jest prawdziwa dla x![]()
R
§7.1 SZEREG FOURIERA DLA FUNKCJI PARZYSTEJ I NIEPARZYSTEJ
Załóżmy, że funkcja f jest funkcją parzystą w przedziale <-l,l>. Wtedy współczynniki a0, an i bn upraszczają się do następującej postaci:
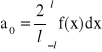
, 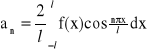
, ![]()
i szereg Fouriera przyjmuje postać:
![]()
Załóżmy, że funkcja f jest funkcją nieparzystą w przedziale <-l,l>. Wtedy współczynniki a0, an i bn upraszczają się do następującej postaci:
![]()
, ![]()
, 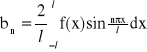
i szereg Fouriera przyjmuje postać:
![]()
Niech funkcja f spełnia warunki Dirichleta w przedziale (0,l).
Przedłużmy tę funkcję w sposób nieparzysty do przedziału <-l,l>,
czyli rozważmy funkcję:
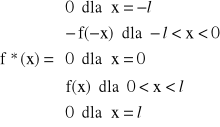
Szereg Fouriera dla funkcji f*(x) przyjmuje postać:
![]()
![]()
, ![]()
, 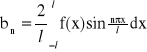
Niech funkcja f spełnia warunki Dirichleta w przedziale (0,l).
Przedłużmy tę funkcję w sposób parzysty do przedziału <-l,l>,
czyli rozważmy funkcję:
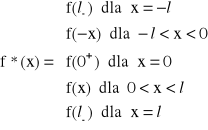
Szereg Fouriera dla funkcji f*(x) przyjmuje postać:
![]()
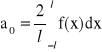
, 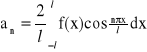
, ![]()
|x0|
x0
-|x0|
y=x2
y=x
y=x3
y=x4
?
?
0
w tych punktach nie wiadomo
zbieżny w tym przedziale
X
X
0
zbieżny
rozbieżny
rozbieżny
X
0
zbieżny
rozbieżny
rozbieżny
-R
+R
?
?
w tych punktach nie wiadomo
0
z b i e ż n y
X
f(x2)
f(x1)
x2
x1
a
b
X
Y
f(x)
-f(-x)
0
X
Y
-l
l
f(x)
f(-x)
0
X
Y
-l
l