Temat : Statyczna próba rozciągania z dokładnym pomiarem

wydłużenia .

Cel ćwiczenia.

Celem ćwiczenia jest zapoznanie się z przyrządami do przeprowadzenia statycznej próby rozciągania z dokładnym pomiarem wydłużeń . Przeprowadzone ćwiczenie pozwoli wyznaczyć nam wartość modułu sprężystości podłużnej E...

Wiadomości wstępne

Badania przeprowadza się na znormalizowanych próbkach , o przekroju kolistym lub prostokątnym . Próbka składa się z części pomiarowej oraz dwóch główek o większym przekroju , służących do mocowania próbki w maszynie . Przejścia między główką a częścią pomiarową są zaokrąglone w celu uniknięcia koncentracji naprężeń

Próbę statycznego rozciągania przeprowadza się na maszynach uniwersalnych lub na maszynach zwanych zrywarkami . Maszyny takie mogą mieć napęd mechaniczny elektryczny lub hydrauliczny. Ten ostatni napęd daje możliwość ciągłej regulacji prędkości rozciągania i amortyzuje drgania i uderzenia powstające przy zerwaniu próbki .

W czasie próby zwiększane jest wydłużenie przez co wzrastają w materiale naprężenia . W początkowym okresie zależność między tymi dwoma wielkościami , naprężeniem i wydłużeniem można opisać prawem Hooke'a .

Próbę statycznego rozciągania z dokładnym pomiarem wydłużeń realizuje się w taki sam sposób jak w prostej próbie rozciągania . Najważniejszą różnicą jest pomiar wydłużeń .

Realizowany jest on za pomocą tensometrów . Są to urządzenia do pomiaru małych wydłużeń . Najczęściej mierzoną , przez tensometry , wielkością jest średnie wydłużenie L , na odcinku o długości początkowej Lo . Długość ta zwana jest bazą tensometru . Wielkością charakteryzującą tensometr jest tzw. stała tensometru . Jest to przyrost długości pomiarowej L do różnicy wskazań tensometru , pomnożone przez odwrotność bazy .

Ogólnie tensometry możemy podzielić na tensometry mechaniczne , optyczne , mechaniczno optyczne akustyczne i elektryczne . Każdy z wymienionych rodzajów zawiera w sobie różne modele różniące się od siebie sposobem pomiaru .

W naszym ćwiczeniu wykorzystany

zostanie mostek tensometryczny

i tensometry elektryczne .

Próbka w odróżnieniu od próbki do poprzedniego ćwiczenia ma przekrój prostokątny . Jest to podyktowane łatwością zamocowania tensometrów .

Wyznaczanie naprężeń granicznych przy umownym wydłużeniu trwałym można realizować dwoma metodami , obciążania i odciążania . Odciążanie polega na stopniowym obciążaniu i odciążaniu próbki i na pomiarze trwałych wydłużeń po każdym odciążeniu . Można na podstawie uzyskanych danych wykreślić zależność między naprężeniem i odkształceniem . Punkty na wykresie układające się w linię prostą obrazują stan naprężeń , w którym obowiązuje prawo Hooke'a . W tym zakresie można wyznaczyć moduł sprężystości podłużnej będący ilorazem naprężenia i odkształcenia . Przyczym moduł E liczy się dla poszczególnych przedziałów biorąc jako wartość końcową średnią . Druga do wyznaczenia wielkość , czyli naprężenie graniczne to wartość siły wywołującej odkształcenie trwałe , wynoszące 0.01%, do przekroju pierwotnego próbki .

Poniżej przedstawiony jest schemat połączenia tensometrów z mostkiem tensometrycznym .

Warunki pomiaru.

Pole przekroju próbki S	100 mm2
Obciążenie początkowe F0	300 daN
Stała tensometru k	2.15
F	10 daN
	0.005

Obliczenia.

Naprężenie dla poszczególnych wartości siły obliczamy z zależności :

Natomiast moduł Younga obliczamy z zależności :

Zestawienie wyników pomiaru.

F			E
daN	‰	MPa	MPa
300	13.89	30	21.6
500	14.08	50	1052.6
700	14.17	70	2222.2
900	14.27	90	2000
1100	14.38	110	1818.2
1300	14.47	130	2222.2
1500	14.59	150	1666.6
1700	14.69	170	2000
1900	14.79	190	2000
2100	14.92	210	1538.5
2300	15.04	230	1666.6
2500	15.18	250	1428.6
2700	15.32	270	1428.6
2900	15.48	290	1250
3100	15.64	310	1250
3300	15.84	330	1000
3500	16.04	350	100
3630	16.40	363	36.11

Analiza błędu metodą najmniejszych kwadratów :

Dla uzyskania dokładnej wartości modułu Younga można zastosować do obliczeń model korelacji liniowej w oparciu o metodę najmniejszych kwadratów. Niezbędne obliczenia potrzebne do wyznaczenia modułu sprężystości podłużnej E przedstawiono w tabelach.

L.p.
1	30	900	13.89	192.9321	416.7	2876755
2	50	2500	14.08	198.2464	704	2238315
3	70	4900	14.17	200.7889	991.9	1679875
4	90	8100	14.27	203.6329	1284.3	1201435
5	110	12100	14.38	206.7844	1581.8	802995.2
6	130	16900	14.47	209.3809	1881.1	484555.2
7	150	22500	14.59	212.8681	2188.5	246115.2
8	170	28900	14.69	215.7961	2497.3	87675.21
9	190	36100	14.79	218.7441	2810.1	9235.21
10	210	44100	14.92	222.6064	3133.2	10795.21
11	230	52900	15.04	226.2016	3459.2	92355.21
12	250	62500	15.18	230.4324	3795	253915.2
13	270	72900	15.32	234.7024	4136.4	495475.2
14	290	84100	15.48	239.6304	4489.2	817035.2
15	310	96100	15.64	244.6096	4848.4	1218595
16	330	108900	15.84	250.9056	5227.2	1700155
17	350	122500	16.04	257.2816	5614	2261715
18	363	131769	16.40	268.96	5953.2	2669629
	3593	908669	912262	1824524	3649048	15846474

Poszukujemy dla tego przypadku zależność liniową w postaci:

y=a+bx

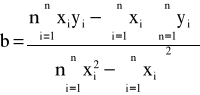
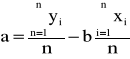
Wstawiając wartości z tabeli otrzymamy

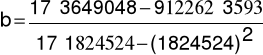
b=0.00096

a=159.83

Równanie y = a+bx rozwiązuje nasze zagadnienie,bowiem współczynnik b określa pochylenie liniowej części krzywej rozciągania.Przeliczona wartość współczynnika

b wyznacza nam średnią wartość modułu sprężystości podłużnej E

E=2,031.105[MPa]

Określenie przedziału ufności

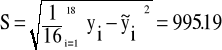
Przyjmując współczyniki
z tablic dla k=16,p=0,95 przedział ufności wygląda następująco :

977.27 < S < 1470.03

Wnioski

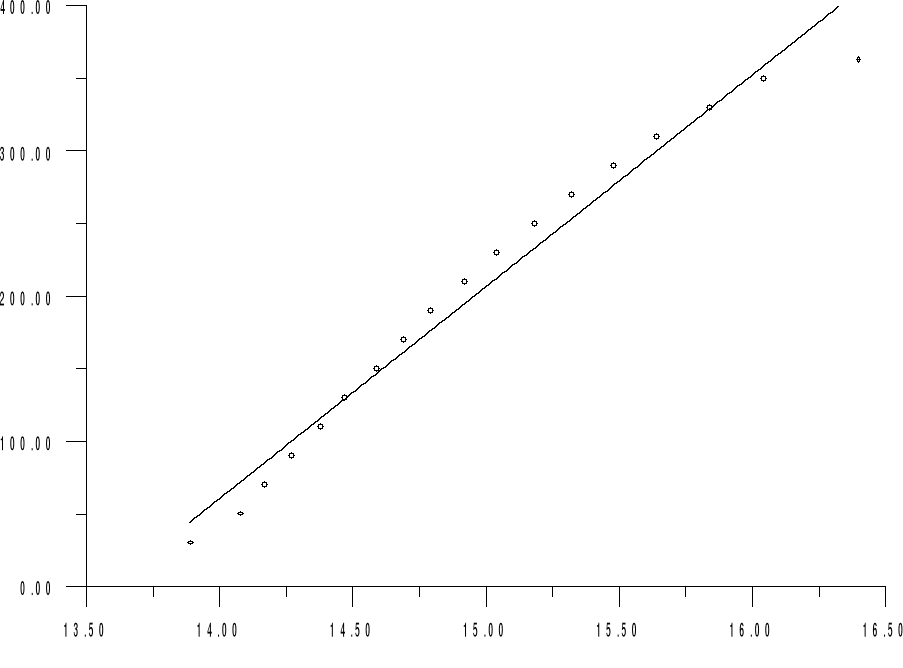
W wyniku pomiarów na wykresie otrzymaliśmy linię prostą, co oznacza , że siły użyte nie spowodowały przekroczenia granicy plastyczności. Punkty na wykresie nie układajią się idealnie w linię prostą , gdyż spowodowane jest to błędami pomiarów. Jednak punkty mieszczą się w przedziale ufności. Możemy dojść do wniosku , że materiał , w zakresie użytych , sił jest plastyczny.

Największy wpływ na wartość błędów mogło mieć wpływ:

- złe zamocowanie tensometru

- niedokładny odczyt z przyrządów mierniczych

- fakt, że dana próbka była już kilkakrotnie poddana próbie rozciągania.

Wykres :

---