DEKOMPOZYCJA SZEREGU CZASOWEGO

CEL ANALIZY SZEREGÓW CZASOWYCH:

poznanie natury rozwoju zjawisk w przeszłości, między innymi w celu przewidywania przyszłości. Główne składniki szeregu czasowego:

A. Tendencja rozwojowa (trend) - ogólny kierunek zmian w czasie, ujawniający się w dość długich okresach, wywołany działaniem przyczyn głównych. Tendencja rozwojowa może być rosnąca, malejąca lub utrzymana (wyrównana).

B. Wahania okresowe - powtarzające się regularnie w kolejnych cyklach zmiany poziomu zjawiska. Szczególnym przypadkiem wahań okresowych są wahania sezonowe, powtarzające się w cyklu rocznym.

C. Wahania przypadkowe - nieregularne zmiany poziomu zjawiska wywołane przyczynami przypadkowymi (losowymi), nie związanymi z istotą badanego zjawiska.

Poziom zjawiska rozpatrywanego w czasie (Y) jest funkcją trendu (
), wahań sezonowych (S) i wahań przypadkowych (E):

Dekompozycja szeregu czasowego - wyodrębnienie trendu (
), wahań sezonowych (S) i wahań przypadkowych (E)

Na ogół przyjmuje się, że składniki szeregu czasowego mają charakter addytywny, tzn. konkretna obserwacja y_t jest traktowana jako suma:

gdzie:

t = 1, 2, ... n - kolejne wyrazy szeregu czasowego;

i = 1, 2, ... d - jednoimienne podokresy w cyklu wahań.

OCENA SKŁADNIKÓW SZEREGU CZASOWEGO:

1. Trend - metoda średnich ruchomych oraz funkcji analitycznych.

1. Wahania sezonowe - metoda wskaźników sezonowości.

2. Wahania przypadkowe - ocena wariancji resztowej i współczynnika zbieżności.

Tendencja rozwojowa (trend) określa ogólny kierunek rozwoju zjawiska w czasie. Wyodrębnianie tendencji rozwojowej odbywa się poprzez oczyszczenie (wygładzenie) szeregu z wszelkich wahań.

Funkcje trendu

Analityczne wyodrębnianie tendencji rozwojowej - szacowanie odpowiedniej funkcji, która w najlepszy sposób odzwierciedla rozwój badanego zjawiska w czasie.

Parametry funkcji obliczane metodą najmniejszych kwadratów, zakładającą minimalizację odchyleń wartości zaobserwowanych (yt) od oszacowanych za pomocą funkcji (
) następująco:

gdzie:

FUNKCJE TRENDU:

A. liniowa:

jest stosowana, gdy występują zbliżone zmiany (przyrosty lub spadki) poziomu zjawiska w kolejnych okresach.

Parametr b określa średni absolutny przyrost (spadek) z okresu na okres,

Parametr a określa teoretyczny poziom zjawiska w okresie t = 0.

B. wykładnicza:

jest wykorzystywana, gdy zmiany poziomu zjawiska są coraz szybsze.

Parametr a określa teoretyczny poziom w okresie t=0, Parametr b określa średni względny przyrost (spadek) poziomu zjawiska z okresu na okres o (b - 1).100%, = średnie tempo zmian.

C. kwadratowa:

jest wykorzystywana, gdy badane zjawisko najpierw rośnie, a potem maleje; bądź też najpierw spada, a potem wzrasta.

Parametry tej funkcji nie mają logicznej interpretacji.

D. hiperboliczna:

stosowana, gdy zmiany badanego zjawiska są coraz wolniejsze, a jego wielkość dąży asymptotycznie do poziomu określonego przez a.

E. logistyczna:

jest funkcją bardzo użyteczną w analizie rynku, np. gdy obserwuje się zmiany popytu na towary wprowadzane na rynek.

Zjawiska, których rozwój w czasie można opisać trendem logistycznym, najpierw rosną wolno, potem coraz szybciej, a wreszcie tempo wzrostu maleje i następuje stagnacja.

Parametr k określa „poziom nasycenia”, do którego dąży badane zjawisko.

Wyodrębnianie wahań przypadkowych (e_t), zawierające w sobie działanie wahań okresowych.

„Reszty”.

Wariancja resztowa:

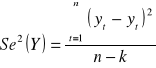
Odchylenie standardowe składnika resztowego:

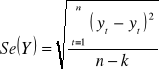
Średnia różnica pomiędzy zaobserwowanymi wartościami w szeregu czasowym i wartościami wyznaczonymi funkcją trendu.

Współczynnik zmienności przypadkowej:

Natężenie wahań przypadkowych w stosunku do średniego poziomu zjawiska.

Współczynnik zbieżności:

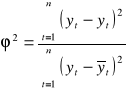
Jaka część zmienności w czasie badanego zjawiska jest spowodowana czynnikami przypadkowymi.

Współczynnik determinacji:

Jaka część zmienności w czasie badanego zjawiska jest wyjaśniona funkcją trendu, czyli jest spowodowana splotem przyczyn (warunków) decydujących o kierunku rozwoju.

Ekstrapolacja szeregu czasowego - przewidywanie poziomu badanego zjawiska w przyszłości.

Warunki stosowania:

• założenie, że zaobserwowana w minionym okresie tendencja rozwojowa będzie zachowana również w przyszłości,

• wpływ czynników przypadkowych będzie zbliżony.

Przedział prognozy dla niezbyt odległych okresów jest zbudowany na podstawie wartości wyliczonych z funkcji trendu
dla przyszłego okresu (t=n+p) oraz wielkości średniego błędu szacunku Se(Y).

Analizując tendencję rozwojową w długich okresach, należy dbać o zapewnienie porównywalności danych. Szczególnej uwagi wymaga ustalenie:

czy nie zmieniły się przyczyny główne, określające tendencję rozwojową;

czy nie uległy zmianom definicje i(lub) sposoby pomiaru badanych zjawisk;

czy zmiany badanego zjawiska w czasie nie są wywołane głównie zmianami cen (inflacją) - dotyczy to wszystkich zjawisk wyrażanych w ujęciu wartościowym (płac, kosztów, obrotów, kredytów itp.)

12

---