Sprawozdanie z wykonanego ćwiczenia nr 320 |
|
|
|
Temat: |
POMIAR PRACY WYJŚCIA TERMOELEKTRONÓW. |
|
|
Imię i nazwisko: |
Jacek Szulc |
|
|
WE |
Semestr: IV |
Rok: II |
|
Zespół: 12 |
Data wykonania: 1996.03.26 |
Ocena: |
Podpis: |
POMIAR PRACY WYJŚCIA TERMOELEKTRONÓW
Prąd nasycenia In odpowiada całkowitemu strumieniowi elektronów emitowanych z katody, jest więc iloczynem gęstości jn prądu emisyjnego i czynnej powierzchni 
katody:
In = jn S
Przy pewnym określonym napięciu anodowym wysokość bariery potencjału staje się równa zeru; odpowiada to napięciu, przy którym wszystkie wyemitowane przez katodę elektrony dotrą do anody. Otrzymamy wtedy prąd nasycenia. Gęstość prądu nasycenia zależy od temperatury katody i wyraża się wzorem Richardsona:
gdzie:
B - stała
T - temperatura katody w kelwinach
A - praca wyjścia elektronu z katody
k- stała Boltzmana
Po uwzględnieniu prawa Richardsona otrzymamy:
W oparciu o prawo Richardsona można wyznaczyć pracę wyjścia elektronu. Zakładając, że znamy dwie wartości prądu nasycenia termoemisji I1 i I2 oraz odpowiadające tym prądom temperatury T1 i T2 możemy napisać:
skąd
Do pomiaru pracy wyjścia wykorzystuje się diodę lampową z katodą wolframową ponieważ charakterystyka prądowo-napięciowa tej lampy wykazuje wyraźne nasycenie prądu anodowego. Aby z wyrażenia wyznaczyć pracę wyjścia elektronu należy znać dwie wartości natężenia prądu nasycenia I1 oraz I2 przy tym samym napięciu anodowym oraz temperaturach żarzenia katody równych T1 i T2. W związku z tym należy sporządzić dwie charakterystyki prądowo-napięciowe lampy przy danych temperaturach żarzenia katody.
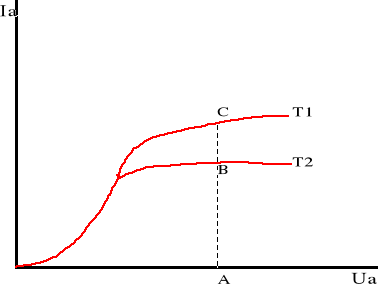
Jak widać z rysunku każdej temperaturze katody odpowiada inne natężenie prądu nasycenia. Im wyższa jest temperatura katody, tym większe jest natężenie prądu nasycenia. Z uzyskanych charakterystyk wyznacza się wartość prądu nasycenia odpowiadające różnym temperaturą katody, ale tej samej wartości napięcia anodowego (na rysunku wartości natężenia prądów odpowiadają odcinkom AB = I1, AC = I2). Temperaturę żarzenia katody można znaleźć wykorzystując zależność oporu katody od temperatury:
RT = R0 (1 + aΔT)
gdzie
RT - opór w temperaturze T
R0 - opór w temperaturze T0
α - temperaturowy współczynnik oporu (dla wolframu α = 0,0046 K-1)
skąd
przy czym T = T0 + ΔT.
Opór RT z dostateczną dokładnością można wyznaczyć z prawa Ohma:
gdzie Iz - prąd żarzenia
Uz - napięcie żarzenia
TABELKA
Numer pomiaru |
Iz = 2,91 Uz = 1,8 |
[A] [V] |
Iz = 2,77 Uz = 1,64 |
[A] [V] |
Iz = 2,7 Uz = 1,56 |
[A] [V] |
Iz = 2,84 Uz = 1,72 |
[A] [V] |
|
Ua [V] |
Ia [mA] |
Ua [V] |
Ia [mA] |
Ua [V] |
Ia [mA] |
Ua [V] |
Ia [mA] |
1 |
5 |
0,6 |
5 |
0,5 |
5 |
0,43 |
5 |
0,53 |
2 |
10 |
1,2 |
10 |
1,0 |
10 |
0,81 |
10 |
1,09 |
3 |
15 |
1,9 |
15 |
1,51 |
15 |
0,95 |
15 |
1,57 |
4 |
20 |
2,6 |
20 |
1,65 |
20 |
0,97 |
20 |
2,3 |
5 |
25 |
3,4 |
25 |
1,69 |
25 |
0,98 |
25 |
2,7 |
6 |
30 |
4,0 |
30 |
1,7 |
30 |
0,99 |
30 |
2,8 |
7 |
35 |
4,4 |
35 |
1,71 |
35 |
1,01 |
35 |
2,8 |
8 |
40 |
4,5 |
40 |
1,71 |
40 |
1,01 |
40 |
2,9 |
9 |
45 |
4,6 |
45 |
1,75 |
45 |
1,02 |
45 |
2,9 |
10 |
50 |
4,6 |
50 |
1,79 |
50 |
1,02 |
50 |
2,91 |
T0 = 273,16 [K]
R0 = 0,06 [Ω]
α = 0,0046 [K-1]
Otrzymane wyniki końcowe
Numer pomiaru |
In [mA] |
RT [Ω] |
T [K] |
ΔR [Ω] |
ΔT [K] |
1 |
4,6 |
0,618 |
2294,89 |
0,013 |
47,10 |
2 |
1,79 |
0,592 |
2200,69 |
0,012 |
43,47 |
3 |
1,02 |
0,577 |
2146,34 |
0,012 |
43,47 |
4 |
2,91 |
0,600 |
2229,68 |
0,014 |
50,72 |
Pomiar |
A [eV] |
ΔA |
A12 |
3,972 |
2,56 |
A13 |
3,920 |
1,789 |
A14 |
2,706 |
2,91 |
A23 |
3,863 |
3,69 |
A24 |
6,700 |
14,88 |
A54 |
13,078 |
3,186 |
A |
6,84 |
5,80 |
a) Wartości prądu nasycenia In odczytane zostały dla wartości napięcia anodowego
Ua = 50 [V]
b) Obliczenia rezystancji katody w temperaturze T dla kolejnych prądów żarzenia zostały obliczone ze wzoru 
1.
2.
3.
4.
Ze wzoru T = T0 + ΔT gdzie , obliczamy kolejno temperaturę katody.
1.
2.
3.
4.
Obliczenia pracy wyjścia termoelektronu
dla każdej pary prądu nasycenia kolejno obliczamy
Analiza błędów
b) ΔT - błędy temperatury katody
Jedynie RT jest obarczone błędem
1.
2.
3.
4.
c) Błąd pracy wyjścia
ΔA12 = 2,56
ΔA13 = 1,78
ΔA14 = 2,91
ΔA24 = 1,88
ΔA34 = 3,69
ΔA23 = 3,18
A = (6,84 ± 1,8) [eV]
WNIOSKI:
Powyższe doświadczenie pozwala przynajmniej w przybliżeniu oszacować wartość pracy wyjścia. Wartość liczbowa obarczona zbyt dużym błędem, aby pomiar traktować ilościowo. Pozwala natomiast na zaobserwowanie zależności pomiędzy prądem anodowym, napięciem anodowym i napięciem żarzenia.
Wyszukiwarka