![]()
Sprawozdanie z ćwiczenia nr C9
Michał Tomaniak Marcin Kmiecik |
Zespół nr 22 |
Wydział Elektryczny |
Ocena z przygotowania: |
Czwartek 1115 - 1400 |
Ocena ze sprawdzenia: |
Data:10 marca, 1994 |
Zaliczenie: |
Prowadzący: K. Mizerski |
Podpis: |
Temat: Wyznaczanie dyspersji optycznej pryzmatu metodą pomiaru kąta najmniejszego odchylenia.
Podstawy teoretyczne.
Celem ćwiczenia jest wyznaczenie wartości kąta łamiącego pryzmatu, oraz wyznaczenie dyspersji optycznej i zdolności rozdzielczej pryzmatu, metodą najmniejszego odchylenia.
Dyspersja optyczna - jest to właściwość polegająca na istnieniu różnej wartości współczynnika załamania światła n dla różnych częstości fali świetlnej :
n=f() lub n=f()
Zjawisko załamania światła - jest to zmiana kierunku biegu wiązki światła, lub zmiana rozchodzenia się fali świetlnej przy przejściu przez granicę dwóch ośrodków.
Zjawiskiem załamania światła oraz jego odbiciem rządzą następujące prawa optyki:
a) kąt padania jest równy kątowi odbicia tzn.
=o
b) stosunek sinusa kąta padania do sinusa kąta załamania jest równy stosunkowi wartości prędkości V1 i V2 światła w danych ośrodkach i jest wielkością stałą n zwaną współczynnikiem załamania ośrodka drugiego względem pierwszego
![]()
Prawo opisane tym wzorem zwane jest prawem Snelliusa.

Jeżeli ośrodkiem z którego wychodzi fala jest próżnia do ośrodka w którym prędkość jest v to powyższy wzór wyraża można zapisać w postaci wyrażającej definicję bezwzględnego współczynnika załamania światła
![]()
Zasada Fermata - promień świetlny biegnący z jednego punktu do drugiego przebywa drogę, na której przebycie potrzeba minimum lub maksimum czasu, albo tę samą ilość czasu.
Zasada ta jest szczególnym przypadkiem zasady obowiązującej przyrodzie, według której wszystkie naturalne procesy przebiegają po drogach optymalnych.
Można ująć to wzorem:
![]()
gdzie n - wsp. załamania światła
s - droga geometryczna (iloczyn L=n.s jest drogą optyczną)

Prawo załamania - ![]()
(rys. wyżej).
W ćwiczeniu tym do zaobserwowania powyższych zjawisk posłużymy się m.in. pryzmatem.
Pryzmat prosty - są to dwie płaszczyzny schodzące się pod kątem , ograniczające jednorodny, przezroczysty materiał. Kąt nazywamy kątem łamiącym pryzmatu.
Pryzmat prosty zawsze rozszczepia wiązkę światła białego jak i zmienia jej bieg.
Działanie pryzmatu oparte jest na zjawisku dyspersji światła.
Każdy pryzmat posiada tzw. zdolność rozdzielczą R , która określa zdolność rozseparowania blisko siebie położonych linii widmowych o długości fali i i wyraża się wzorem : ![]()
Ze wzoru wynika, że zdolność rozdzielcza pryzmatu jest proporcjonalna do dłg. podstawy pryzmatu h i szybkości zmiany wsp. załamania wraz ze zmianą dłg. fali, czyli tzw. dyspersji materiałowej Dn.
Wykonanie ćwiczenia.
1. Ustawienie spektrometru :
- nastawienie krzyża lunety na ostrość
- nastawienie lunety na nieskończoność tzn. na ostrość obrazu dalekiego przedmiotu
- nastawienie kolimatora na ostry obraz oświetlonej szczeliny (wtedy szczelina jest w ognisku soczewki kolimatora).
- wypoziomowanie stolika spektrometru
2. Ustawiamy pryzmat na stoliku spektrometru i oświetlamy szczelinę spektrometru światłem sodowym.
3. Mierzymy kąt łamiący pryzmatu.()
Ustawimy pryzmat w takim położeniu, żeby kąt łamiący znalazł się naprzeciwko kolimatora. Następnie obserwujemy w lunetce obrazy szczeliny wytworzone przez promienie odbite od ścianek pryzmatu. Ustawiamy lunetkę na obserwację wiązki odbitej od jednej ścianki pryzmatu i odczytujemy położenie "a" lunetki, następnie obserwujemy wiązkę odbitą od drugiej ścianki pryzmatu, odczytując położenie "b" lunetki. Pomiary powtarzamy 3 razy.
Kąt łamiący jest równy połowie różnicy tych odczytów tzn.
![]()
4. Wyznaczamy kąt najmniejszego odchylenia promieni przez pryzmat (![]()
).
Najpierw wykonujemy pomiary dla światła sodowego.
Manipulując stolikiem i lunetką nastawiamy lunetkę na położenie najmniejszego odchylenia dla kąta łamiącego , wcześniej przez nas wyliczonego. Obserwujemy, że w pewnym położeniu stolika prążek zatrzymuje się i przy dalszym obrocie stolika wraca.
Ustawiamy stolik w położeniu zwrotnym i odczytujemy kąt na obu noniuszach.
Jednocześnie wyznaczamy tzw. martwy przedział (m.p), czyli taki kąt obrotu stolika kiedy oko nie dostrzega zmian położenia prążka.
Następnie zdejmujemy pryzmat i ustawiamy lunetkę na wprost kolimatora, odczytując kąty na obu noniuszach A i B.
Identyczne pomiary wykonujemy dla światła Neonu tzn dla dwóch prążków: żółtego i zielonego. Wszystkie pomiary wykonujemy trzykrotnie a wyniki zapisujemy w tabeli.
Szukany kąt najmniejszego odchylenia promieni przez pryzmat jest równy różnicy kątów położenia lunetki w najmniejszym odchyleniu i położenia lunetki na wprost kolimatora.
Mając te dane obliczamy współczynnik załamania ze wzoru:
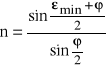
Wartości i ![]()
przyjmujemy jako średnie arytmetyczne ze wszystkich pomiarów.
Dyskusja błędów.
1. Znajdujemy błąd kąta łamiącego pryzmatu
![]()
gdzie: 2' - dokładność odczytu kąta
sz - szerokość kątowa obrazu szczeliny sz=8'
Po podstawieniu otrzymujemy:
![]()
2. Znajdujemy błąd kąta najmniejszego odchylenia ![]()
![]()
gdzie: sz - jw
(m.p) - martwe pole (m.p)=26'
Po podstawieniu otrzymujemy:
![]()
3. Znajdujemy błąd bezwzględny pomiaru pośredniego n
Korzystamy ze wzoru 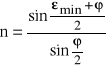
Czyli:
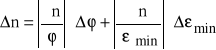
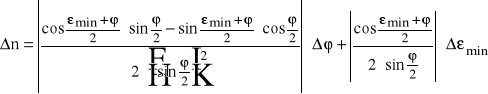
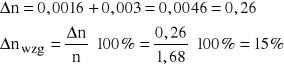
Ostatecznie wyliczony współczynnik załamania światła wynosi n=1,680,26
Laboratorium z Fizyki.
Błąd! Nieznany argument przełącznika.