Laboratorium fizyki
Ćwiczenie nr O3 Wyznaczanie współczynnika załamania światła za pomocą refraktometru Abbego
ZSZ-PC-6	GRUPA II	Derlatka Magdalena Herka Karol
16.V.2004	Ocena :

1.Wstęp

Celem ćwiczenia jest wyznaczenie współczynnika załamania dla różnych cieczy a następnie wyliczenie kata granicznego.

Dla jednej z cieczy wskazanej przez prowadzącego badamy zależność współczynnika załamania od temperatury i na podstawie pomiaru wykonujemy wykres.

Niech na monochromatyczna fala świetlna pada na gładką powierzchnię rozdzielającą dwa przezroczyste te ośrodki.

α

I

II

β

Oznaczamy przez V_I i V_II prędkości rozchodzenia się światła odpowiednio w ośrodkach I i II, a n_I i n_II odpowiednie współczynniki załamania. Wówczas

lub

Wzory te opisują prawo załamania zwane prawem Snelliusa. Jeżeli pierwszym ośrodkiem jest powietrze, to możemy przyjąć że n_I wynosi 1.

Fala świetlna rozchodząca się w ośrodku optycznie rzadszym pada na granicę z ośrodkiem optycznie gęstszym i załamuje się w kierunku do normalnej. Biorąc pod uwagę zasadę o odwracalności biegu promieni świetlnych, możemy przeanalizować sytuację odwrotną, tzn taką, gdy fala świetlna rozchodząca się w ośrodku optycznie gęstszym, pada na granicę z ośrodkiem optycznie rzadszym. Wówczas kat załamania jest większy od kąta załamania. Odpowiadający mu kąt padania nazywamy katem granicznym, ponieważ dla każdego kąta padania większego od kąta granicznego nastąpi całkowite odbicie wewnątrz ośrodka optycznie gęstszego. Kat graniczny jest określony, zgodnie z prawem Snelliusa, następującym wzorem:

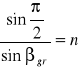
Pomiar kąta granicznego może być wykorzystany do współczynnika załamania. Na tej zasadzie oparta jest budowa refraktometru Abbiego.

Refraktometr umieszczony jest na stole oświetlonym biały światłem rozproszonym. Za pomocą pipetki nanosimy kilka kropel badanej cieczy na pryzmat P₂ , a pryzmat P₁ zamykamy. Miedzy pryzmatami wytwarza się płasko równoległa warstewka cieczy. Na ogół granica ta będzie otoczona obwódką, znajdującą się na skrzyżowaniu nitek pajęczych.

Następnie odczytujemy wartość współczynnika załamania n .

2.Obliczenia:

Nazwa cieczy	Współczynnik załamania
		1	2	3	4	5	Średnia	Błąd odczytu
1. Woda	1,334	1,334	1,334	1,334	1,334	1,334	∆n=0,001
2. Denaturat	1,372	1,372	1,372	1,372	1,372	1,372	∆n=0,001
3.Olej silnikowy	1,558	1,558	1,558	1,558	1,558	1,558	∆n=0,001
4.Olej przekładniowy	1,490	1,490	1,490	1,490	1,490	1,490	∆n=0,001

Nazwa cieczy	Współczynnik załamania
		T1	T1+3^0C	T1+6^0C	T1+9^0C	T1+12^0C	T1+15^0C	T1+18^0C
Olej przekładniowy	21^0C	24^0C	27^0C	30^0C	33^0C	36^0C	39^0C
	1,490	1,490	1,489	1,488	1,486	1,486	1,485

T1+21^0C	T1+24^0C	T1+27^0C	T1+30^0C	∆T=1^0C
42^oC	45^0C	48^0C	51^0C	∆n=0,001
1,484	1,482	1,482	1,480

3.Wnioski:

Uniwersalny refraktometr Abbiego pozwala na użycie światła białego. W zależności od rodzaju cieczy, od jej stopnia gęstości wyróżniamy różne współczynniki załamania. Jeżeli fala świetlna rozchodząca się w ośrodku optycznie gęstszym, pada na granicę z ośrodka optycznie rzadszego, wówczas kąt załamania jest większy od kąta padania.

---