Sprawozdanie z ćwiczenia nr C-4

Temat: Badanie odbicia światła od powierzchni dielektryków.

Podstawy teoretyczne.

1. Fale elektromagnetyczne.

Falą nazywane jest przemieszczające się w przestrzeni zaburzenie wielkości fizycznej. Dla fal na powierzchni wody zaburzeniem jest zmiana wysokości poziomu wody względem poziomu równowagi. Światło jest również falą a zmianie ulegają natężenia pól elektrycznego i magnetycznego. Najprostszym rodzajem takiej fali jest zaburzenie okresowe o częstości nazywane falą monochromatyczną. Natężenie pola elektrycznego i magnetycznego dla fali monochromatycznej w dowolnym punkcie przestrzeni zmienia się w czasie proporcjonalnie do funkcji cos(t) a oscylacje te przesuwają się ze stałą prędkością v. Wektor natężenia pola elektrycznego monochromatycznej fali elektromagnetycznej rozchodzącej się w kierunku 0X opisany jest wzorem:

gdzie:
- amplituda natężenia pola elektrycznego, (t-kx) - faza fali,

k=/v -liczba falowa.

Wartość natężenia pola magnetycznego zmienia się w analogiczny sposób, z tym tylko, że liczba falowa ma postać k=2/.

Pole elektryczne i magnetyczne opisywane są za pomocą wektorów, dlatego też należy oprócz i wartości określić kierunek. Jednak samo określenie kierunku rozchodzenia się fali elektromagnetycznej nie wyznacza dokładnie kierunków wektorów natężenia pola elektrycznego i magnetycznego. Określenie tych kierunków wiąże się z polaryzacją światła.

2. Polaryzacja światła.

Kierunek wektorów natężenia pola elektrycznego i magnetycznego fali elektromagnetycznej może zmieniać się w czasie. Jeżeli kierunek drgań tych wektorów w danym punkcie zmienia się przypadkowo, to światło nie jest spolaryzowane.

Dla światła spolaryzowanego kierunek wektorów natężenia pola jest stały lub zmienia się w ściśle określony sposób. Fala elektromagnetyczna jest spolaryzowana liniowo gdy kierunek natężenia pola elektrycznego i prostopadłego do niego magnetycznego jest stały i jednakowy dla wszystkich punktów na drodze rozchodzenia fali.

Poza polaryzacją liniową występuje tak zwana polaryzacja kołowa lub eliptyczna w której wektory pola elektromagnetycznego obracają się wokół kierunku rozchodzenia się fali i mogą zmieniać przy tym swoją długość..

Każdy stan polaryzacji można uzyskać poprzez złożenie dwóch fal spolaryzowanych liniowo w kierunkach wzajemnie prostopadłych o odpowiednio dobranej różnicy faz.

Do wytwarzania ( i badania) światła spolaryzowanego wykorzystuje się polaryzatory, które są elementami przepuszczającymi światło tylko w określonym kierunku polaryzacji.

Jeżeli kierunek polaryzacji tworzy z osią polaryzatora kąt , to jest przepuszczana ta cześć fali elektromagnetycznej określonej przez rzut wektora natężenia pola fali elektromagnetycznej na kierunek osi polaryzatora. Rzut wektora natężenia pola elektrycznego na kierunek tworzący z nim kąt wynosi Eocos. Ponieważ natężenie światła jest proporcjonalne do kwadratu amplitudy, to natężenie światła przechodzącego przez polaryzator wynosi:

gdzie: Io - natężenie światła padającego na polaryzator.

Powyższe równanie stanowi prawo Malusa.

3. Rozchodzenie się światła w dielektrykach.

Dielektryki są ośrodkami w których nie ma swobodnie poruszających się ładunków. Zewnętrzne pole elektryczne rozsuwa ładunki dodatnie i ujemne, tworząc w ten sposób dipole elektryczne. Pole elektryczne fali elektromagnetycznej indukuje dipole drgające z częstością taką samą jak częstość drgań pola tej fali. Z kolei każdy drgający dipol staje się źródłem promieniowania elektromagnetycznego - wytwarza falę wtórną nakładającą się na falę padającą.

Mechanizm ten powoduje, że wypadkowa fala elektromagnetyczna porusza się z mniejszą prędkością niż w próżni a kierunek jej rozchodzenia jest inny niż kierunek fali pierwotnej.

Stosunek prędkości fali w próżni c do prędkości monochromatycznej fali wypadkowej w danym ośrodku definiuje się jako współczynnik załamania światła n=c/. Określa on własności optyczne związane z oddziaływaniem fali elektromagnetycznej z materią.

Jeśli ośrodek w którym rozchodzi się światło jest niejednorodny to niektóre z indukowanych drgających dipoli wysyłają promieniowanie wtórne w przypadkowych kierunkach i światło ulega rozproszeniu. Przypadkowość ta ma jednak ograniczenie tzn drgający dipol elektryczny nie emituje fali elektromagnetycznej w kierunku wzdłuż którego sam drga. Dzięki tej właściwości można jakościowo określić kierunek polaryzacji światła liniowo spolaryzowanego, obserwując natężenie światła rozpraszanego przez ośrodek rozpraszający.

4. Odbicie i załamanie światła.

Światło przechodząc z jednego ośrodka do drugiego o innym współczynniku załamania ulega odbiciu i załamaniu. Kąt odbicia jest równy kątowi padania. Zależność tę opisuje prawo Snelliusa :

gdzie:  - kąt padania w ośrodku o współczynniku załamania n1,

 - kąt padania w ośrodku o współczynniku załamania n2

Powyższe prawo określa jedynie kierunki rozchodzenia się fal odbitej i załamanej w stosunku do kierunku rozchodzenia się fali padającej i płaszczyzny rozgraniczającej ośrodki.

Nie określa natomiast tego, jaka część natężenia padającego światła ulega odbiciu, a jaka część przechodzi do innego ośrodka. Tę właściwość określa współczynnik odbicia R, będący stosunkiem natężenia odbitego światła do natężenia światła Io padającego na granicę ośrodków. Wartość współczynnika odbicia R zależy od kąta padania i wartości współczynników załamania w obu ośrodkach a także zależy od polaryzacji fali padającej.

Geometria układu wyróżnia tu dwa graniczne przypadki polaryzacji liniowej.

Obrazuje to poniższy rysunek.

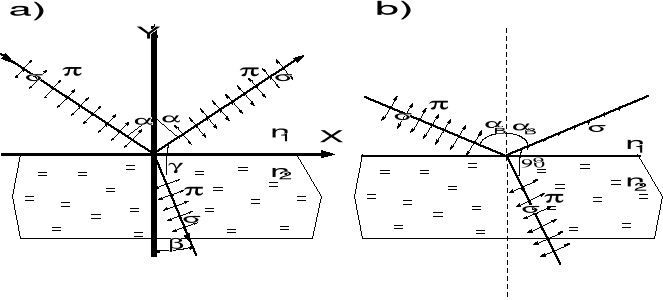
Rys. Odbicie i załamanie światła na granicy dwóch dielektryków. Strzałkami - dla polaryzacji

i kropkami dla polaryzacji zaznaczone są kierunki drgań wektora natężenia pola elektrycznego fali świetlnej. Rysunek b) przedstawia przypadek padania światła pod kątem Brewstera B.

Fala odbita ma wówczas polaryzację

Współczynniki odbicia dla obu polaryzacji tzn. i są określone przez wzory Fresnela:

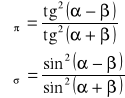
gdzie: i - kąty padania i odbicia powiązane ze sobą przez prawo Snelliusa.

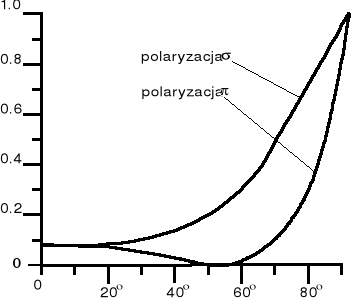
Wzory Fresnela otrzymuje się z równań Maxwella, stanowiących podstawowe równania opisujące własności pola elektromagnetycznego. Poniżej pokazane są wykresy zależności współczynników odbicia R, R od kąta padania:

5. Własności światła odbitego od powierzchni dielektryków.

Dal światła padającego na granicę rozdzielającą ośrodki pod kątem =0 współczynniki odbicia dla obu polaryzacji i są sobie równe a ich wartość wynosi:

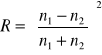
Ze wzoru tego wynika, że wartość współczynnika odbicia światła padającego prostopadle do powierzchni jest niezależna od tego z której strony pada światło na granicę ośrodków, tzn. jest taki sam dla światła przechodzącego z powietrza do szkła jak i od strony szkła do powietrza ( obrazują to powyższe wykresy).

Dla kątów padania większych od zera współczynniki odbicia stają się różne dla różnych polaryzacji.

Wraz ze wzrostem kąta padania wartości współczynników odbicia dla obu polaryzacji zmieniają się w różny sposób. Dla polaryzacji współczynnik odbicia rośnie do R=1

dla =90 co oznacza, że światło porusza się równolegle do granicy ośrodków i nie występuje fala załamana. Natomiast dla polaryzacji współczynnik odbicia najpierw maleje, dla kąta padania B osiąga wartość zerową ( czyli natężenie światła odbitego jest równe zero) a dopiero później wzrasta.

Kąt padania B dla którego nie ma fali odbitej o polaryzacji nazywa się kątem Brewstera.

Zerowanie się współczynnika odbicia R następuje w przypadku gdy suma kątów padania i odbicia wynosi 90. Warunek ten oznacza, że fala załamana i odbita są względem siebie prostopadłe. Na skutek tego, że indukowane dipole nie mogą wysyłać fali wtórnej w kierunku drgań własnych to w kierunku w którym powinna pojawić się fala odbita nie wysyłane są fale wtórne i stąd fala odbita nie występuje.

Odpowiadający kątowi Brewstera kąt załamania wynosi =90-B czyli po podstawieniu do prawa załamania otrzymuje się:

a stąd:

6. Całkowite wewnętrzne odbicie.

Odbicie światła na granicy dwóch ośrodków występuje zawsze oprócz przypadku zjawiska Brewstera. Przechodzenie światła do drugiego ośrodka i obserwowany przy tym efekt załamania może się natomiast odbywać tylko w pewnym zakresie kątów padania. Ograniczenie to ma miejsce, gdy światło pada od strony ośrodka o większym współczynniku załamania np. dla padania od strony szkła o wsp. załamania n1 na granicę z powietrzem, którego wsp. załamania wynosi n2=1. Wartości współczynnika odbicia światła osiąga wówczas wartość maksymalną R=1 dla kąta padania GR. Dla kątów większych od GR światło ulega całkowitemu wewnętrznemu odbiciu. Granicznym kątem padania jest kąt, dla którego fala załamana porusza się wzdłuż granicy rozdzielającej oba ośrodki skąd wniosek:

Wykonanie ćwiczenia.

1. Dokonujemy wzrokowej obserwacji stanu polaryzacji światła, przepuszczając wiązkę światła przez polaryzator oraz naczynie z koloidalną zawiesiną tj. herbatą.

Następnie obracając polaryzatoremu wokół osi wiązki (czyli zmieniając kierunek polaryzacji) obserwujemy smugę światła w naczyniu, patrząc z boku lub z góry naczynia.

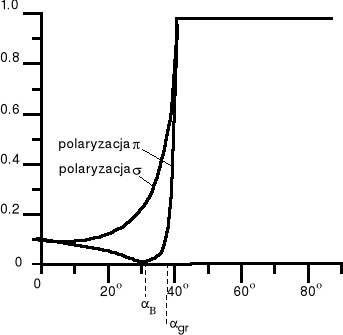
2. Dokonujemy pomiaru natężenia światła odbitego od powierzchni szklanej płytki dla różnych kątów padania, oświetlając płytkę światłem o polaryzacji . Szukamy kąta Brewstera w ten sposób, że obserwujemy przy jakim kącie padania natężenie światła (mierzone poprzez fotodetektor i odczytywane na mikroamperomierzu) spadnie do zera.

Wykonujemy wykres zależności fotoprądu od kąta padania. Z wykresu wyznaczamy graficznie kąt Brewstera.

W naszym przypadku otrzymaliśmy:

- kąt Brewstera B=56

3. Znając kąt Brewstera obliczamy współczynnik załamania szkła. Korzystamy ze wzoru:

gdzie: n1 - wsp. załamania powietrza n1=1

n2 - szukany wsp. załamania szkła.

Po podstawieniu i obliczeniu otrzymaliśmy:

nszkła=1,48

3. Dokonujemy pomiarów jak w punkcie 2 dla polaryzacji . Sporządzamy wykres zależności fotoprądu od kąta padania światła.

4. Przy użyciu dwóch polaryzatorów sprawdzamy słuszność prawa Malusa tzn. ustawiamy tak polaryzatory aby natężenie światła przechodzącego było maksymalne (kierunki osi polaryzatorów są wówczas równoległe). Znajdujemy kąt o jaki należy obrócić jeden z polaryzatorów aby natężenie światła spadło do połowy maksymalnej wartości.

Znaleziony kąt to =43

Dyskusja błędów.

Szacujemy graficznie niepewność pomiarową B z wykresu zależności fotoprądu od kąta padania, co pozwala nam jednocześnie oszacować niepewność pomiarową n.

n=0,12

nwzgl=8%

Ostatecznie:

nszkła=1,480,12

Laboratorium z Fizyki.

Strona nr 6

---