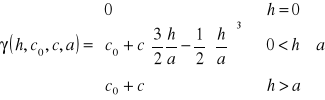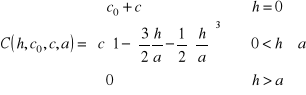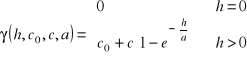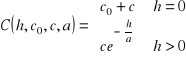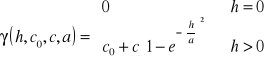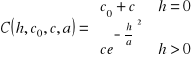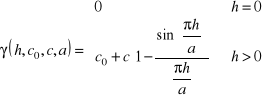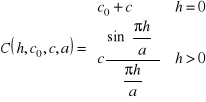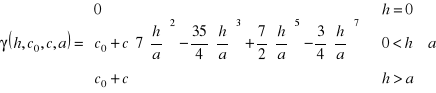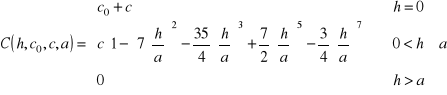Stacjonarność 2-go rzędu

Pole losowe jest stacjonarne 2 - rzędu, jeżeli:

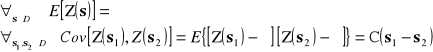
Wartość oczekiwana pola losowego jest stała w całej dziedzinie D, oraz funkcja kowariancji nie zależy od położenia a od wektora przesunięcia h pomiędzy Z(s₁) and Z(s₂) = Z(s₁ + h). Istnienie funkcji kowariancji pociąga za sobą istnienie skończonej wariancji C(0) = Cov[Z(s),Z(s+h)] = V[Z(s)] dla h = 0.

Funkcję kowariancji pola losowego stacjonarnego 2-go rzędu można zapisać jako:

Dla stałej i równej zero wartości oczekiwanej pola losowego:

Formuła na kowariancję upraszcza się do poniższego wzoru:

Stacjonarność wewnętrzna

Pole losowe jest stacjonarne wewnętrznie, jeżeli:

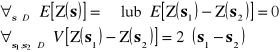
Zatem wartość oczekiwana oraz wariancja przyrostów pola losowego są niezależne od położenia a jedynie od wektora przesunięcia. Funkcja 2γ nazywa się wariogramem, γ - semiwariogramem. Semiwariogram jest podstawową funkcją używaną w geostatystyce do opisu struktury pola losowego. Ma przewagę w stosunku do kowariogramu (funkcji kowariancji) ponieważ opisuje szerszą klasę zjawisk oraz w procesie estymacji nie wymaga znajomości wartości oczekiwanej pola losowego. Dla powyższych założeń wariogram może zostać zapisany, jako:

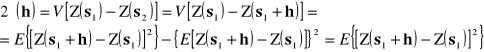
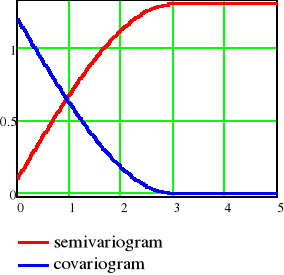
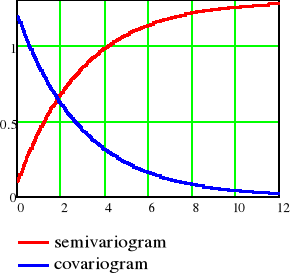
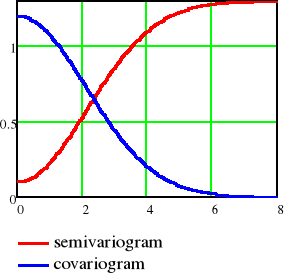
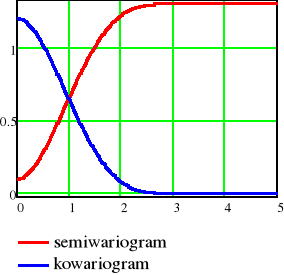
Podstawowa funkcja geostatystyki - semiwariogram ujawnia jak bardzo różnią się wartości Z(s) oraz Z(s+h), wraz ze wzrostem odległości h. Wykres semiwariogramu dostarcza informacji o ciągłości oraz przestrzennej zmienności pola losowego. Podobnie jak w I prawie geografii podanym przez Waldo Toblera w 1972, "wszystkie obiekty są powiązane, ale te bliższe bardziej niż te odległe", wykres semiwariogramu opisuje jak zmienia się podobieństwo atrybtów wraz ze wzrostem odległości, oczekujemy, że wraz ze wzrostem odległości wartości semiwariogramu również będą rosnąć.

Wykres typowego semiwariogramu dla pól losowych stacjonarnych drugiego rzędu przedstawiono na poniższym rysunku:

Związek między kowariancją a semiwariancją dla procesów stacjonarnych rzędu drugiego

Dla procesów stacjonarnych 2 rzędu (z funkcją kowariancji) występuje zależność między tymi dwiema funkcjami struktury. Wychodząc z definicji wariogramu i korzystając ze stacjonarności 2 - go rzędu możemy zapisać:

Co w wyniku daje nam:

Wielkości charakterystyczne semiwariogramu (funkcji kowariancji)

Semiwariogram charakteryzuje się pewnymi wielkościami i własnościami:

• zakres, strefa oddziaływania, promień autokorelacji (range) ိ w przypadku pól losowych stacjonarnych drugiego rzędu wygląd semiwariogramu jest bardzo charakterystyczny (semiwariogramy ograniczone, ang. bounded semivariogram), wartości semiwariogramu γ(h) rosną wraz ze wzrostem odległości h, osiągając pewną wartość progową (sill). Wartość progowa jest osiągana dokładnie lub jedynie asymptotycznie. Odległość h, przy której wykres semiwariogramu zaczyna sie stabilizować, osiąga próg, nazywa się zakresem lub strefą oddziaływania (range, zone of influence). Dla odległości h większych niż zakres a autokorelacja przestrzenna nie występuje (lub jest zaniedbywalna). Dla semiwariogramów osiągających próg jedynie asymptotycznie definiuje się zakres praktyczny (practical range) jako taką odległość h, dla której γ(h) = 0.95⋅
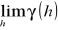
  . Nie wszytkie semiwariogramy osiągają wartość progową, niektóre rosną nieograniczenie (ang. unbounded semivariograms). Powodem tego może być między innymi: niestacjonarność procesu (trend, zmienna - zależna od położenia wartość oczekiwana), proces jest procesem wewnętrznie stacjonarnym.

• próg lub częściowy próg dla modeli z efektem samorodków (sill, partial sill) ိ wypłaszczenie jakie osiąga semiwariogram poza zakresem (asymptota pozioma)

• "efekt samorodków" (nugget effect) ိ bardzo często w praktyce wykres semiwariogramu nie przechodzi przez początek układu współrzędnych, przesunięcie wykresu semiwariogramu na osi rzędnych (y) w kierunku dodatnim nazywa się "efektem samorodków" i oznacza się zwyczajowo jako c_o. Zapisując powyższe w języku matematyki dostajemy:
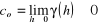
  . "Efekt samorodków" tłumaczony jest błędami pomiarowymi oraz tym, że dysponujemy jedynie skończoną liczbą obserwacji i nie możemy udzielić odpowiedzi jak zachowuje sie proces przy odległościach mniejszych niż minimalna odległość między obserwacjami w rozpatrywanej dziedzinie przestrzennej D. Efekt ten nazwano "efektem samorodków" ponieważ został zauważony po raz pierwszy w pokładach złota w Południowej Afryce a jego wystąpienie było powiązane z występującymi samorodkami złota.

• zachowanie semiwariogramu w początku układu współrzędnych ိ z punktu widzenia modelowania przestrzennej ciągłości oraz przestrzennego zróżnicowania procesu losowego bardzo ważna jest analiza zachowania się semiwariogramu w początku układu współrzednych, h→0. Można wyróżnić:

1. funkcję kwadratową - wskazuje wysoce gładkie pole losowe, kształt funkcji kwadratowej może również świadczyć o obecności dryftu (trendu)

2. funkcję liniową - pole losowe ciągłe ale nie różniczkowalne, proces zachowuje się mniej regularnie niż opisany powyżej

3. nieciągłość w początku układu współrzędnych ("efekt samorodków") ိ
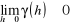
   , relacja ta wskazuje na nieregularny proces na niewielkich odległościach

4. funkcję liniową równoległą do osi odciętych ("czysty efekt samorodków") ိ zachowanie takie wskazuje na czystą losowość (biały szum), brak autokorelacji przestrzennej

Model sferyczny

gdzie poszukiwanymi parametrami modelu semiwariogramu teoretycznego są, θ = [c­­_o, c, a], c­­_o ≥ 0, c ≥ 0, a > 0. Model sferyczny jest często spotykanym w praktyce modelem teoretycznym semiwariogramu, zachowuje się liniowo przy zbliżaniu się do początku układu współrzędnych, co zgodnie z tym co napisano wyżej sugeruje dość regularną strukturę pola losowego. Osiąga próg (sill) dokładnie.

Model eksponencjalny

gdzie poszukiwanymi parametrami modelu semiwariogramu teoretycznego są, θ = [c­­_o, c, a], c­­_o ≥ 0, c ≥ 0, a > 0. Należy również do klasy modeli przejściowych (ograniczonych, tych, które osiągają próg), rośnie mniej gwałtownie niż wspomniany wyżej semiwariogram sferyczny. Osiąga próg jedynie asymptotycznie, stąd też zakres praktyczny (practical range) opisany wyżej (γ(h) = 0.95⋅σ²) wynosi 3⋅a.

Model gaussowski

gdzie poszukiwanymi parametrami modelu semiwariogramu teoretycznego są, θ = [c­­_o, c, a], c­­_o ≥ 0, c ≥ 0, a > 0. Zachowuje sie parabolicznie (funkcja kwadratowa) blisko początku układu współrzędnych, co zgodnie z tym co napisano powyżej sugeruje wysoce ciągły proces losowy. U Wackernage'a (Wackernagel 2003, str. 55) można znaleźć nawet stwierdzenie, że jest to model patologiczny, odpowiada deterministycznej funkcji losowej, która stoi w sprzeczności z losowością. Podobnie jak opisany powyżej model eksponencjalny, semiwariogram gaussowski osiaga próg jedynie asymptotycznie z zakresem praktycznym √3⋅a

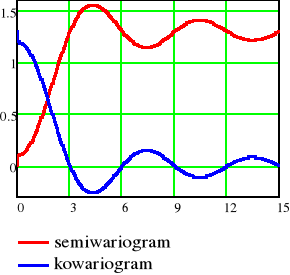
Model sinusowy z „efektem dziury”

Model kubiczny

Podstawowe warianty krigingu

kriging prosty (simple kriging) - stała i znana wartość oczekiwana pola losowego

kriging zwyczajny (ordinary kriging) - stała ale nieznana wartość oczekiwana pola losowego

kriging uniwersalny (universal kriging) - zmienna, zależna od położenia (trend) wartość oczekiwana pola losowego, najczęściej modelowana wielomianami niskiego stopnia (do 3-go)

Zasada konstruowania predyktorów w metodzie krigingu:

1.Nieobciążoność !!!

2. Minimalizacja średniokwadratowego błędu predykcji/estymacji !!!

Kriging zwyczajny (ordinary kriging)

Kriging zwyczajny jako dokładny predyktor

W krigingu zwyczajnym zakłada się stałą, ale nieznaną wartość oczekiwaną pola losowego (danych). Zakładamy, iż pole losowe (dane) podlegają dekompozycji na dwa składniki: wartość oczekiwana oraz zakłócenie. Taki model dekompozycji dotyczy zarówno obserwacji jak i wielkości predykowanych, czyli:


dla obserwowanych (1)


dla predykowanych

Predyktor krigingu zwyczajnego wyraża się za pomocą liniowego związku postaci (kombinacja liniowa obserwowanych danych):


(2)

Biorąc pod uwagę (1) oraz (2) błąd predykcji otrzymujemy w następującej postaci:


(3)

Stąd natychmiast otrzymujemy warunek na nieobciążoność predyktora postaci:


(4)

Poprzez powyższy warunek sumowania się wag krigingu do jedności nieznana wartość procesu losowego jest “usuwana” z procedury optymalizacyjnej. Tym razem procedura minimalizacji średnokwadratowego błędu predykcji jest procedrą warunkową - z warunkiem na nieobciążoność predyktora. Aby otrzymać optymalny w sensie minimum błędu predykcji zestaw współczynników λ wykorzystujemy metodę mnożników Lagrange'a - czyli budujemy funkcję Lagrange'a postaci:


(5)

gdzie: κ - mnożnik Lagrange'a,

Minimalizacja (5) ze względu na λ oraz κ prowadzi do następującego układu równań:


(6)

Rozwiązując powyższy układ równań ze względu na wektor wag krigingu λ oraz mnożnik Lagrange'a κ otrzymujemy:


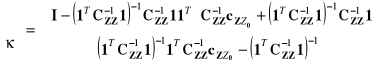
(7)

Wstawiając otrzymany wynik do formuły (2) dostajemy jawne przedstawienie predyktora krigingu zwyczajnego:


(8)

gdzie:


oraz wariancję predykcji postaci:


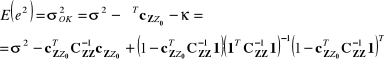
(9)

Kriging zwyczajny jako filtr

Zakładamy, że pole losowe jest stacjonarne rzędu drugiego (stała wartość oczekiwana, funkcja kowariancji zależna jedynie od wektora przesunięcia, skończona wariancja). Rozważamy tym razem model „trend, sygnał i szum”. Zatem obserwacje podlegają następującej dekompozycji:




gdzie: S - całkowity sygnał, suma wartości oczekiwanej μ oraz sygnału s. lokalizację oznaczamy przez u.

Dalej zakładamy, iż:




oraz, że:


, czyli brak korelacji między szumem i sygnałem.

Predykcji podlega całkowity sygnał, czyli „wolna” od szumu wersja Z, zatem (predykcja pojedynczej wielkości):




Wykorzystujemy liniowy (homogenicznie (jednorodnie) liniowy) predyktor całkowitego sygnału, czyli:




Błąd predykcji jest różnicą między predyktorem sygnału a jego nieznaną wartością, czyli:




Zatem wartość oczekiwana błędu predykcji jest równa:




Stąd, aby średnio nie popełniać błędu predykcji, czyli aby był on średnio równy „zero” dostajemy warunek nieobciążoności:




Wstawiając powyższy warunek do wzoru na błąd predykcij dostajemy:




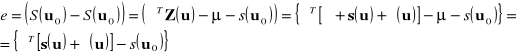
Wówczas średniokwadratowy błąd predykcji można przedstawić jako:




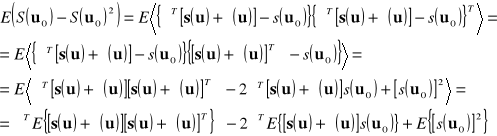
Czym są poszczególne elementy powyższego wzoru:










Minimalizacja średniokwadratowego błędu predykcji przy warunku nieobciążoności:









Powyższy układ równań w postaci macierzowej:




Odwrotność macierzy blokowej




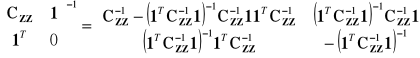
Zatem, rozwiązanie powyższego układu równań ze względu na wektor współczynników λ oraz mnożnik Lagrange'a κ można zapisać jako:




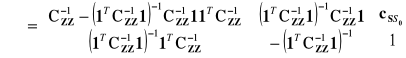
Biorąc powyższe pod uwagę, predyktor całkowitego sygnału można przedstawić, jako:




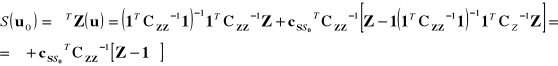
Proszę zwrócić uwagę na podobieństwo do predyktora krigingu zwyczajnego, jako dokładnego interpolatora!!!

Wariancję predykcji sygnału można, zatem zapisać jako:




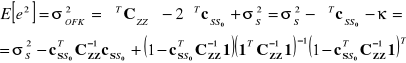
Przykład:

Korzystając z metody krigingu zwyczajnego dokonać predykcji w punkcie x₀, y₀.

Rozmieszczenie punktów:




Dane:




Przyjąć eksponencjalny model funkcji kowariancji z parametrami:

c₀ = 0.05

c = 1.20

a = 3.50




---