1. Ilość przedziałów klasowych :

k=5logN, R=X_max-X_min

Rozpiętość przedziałów klasowych

a) wskaźnik struktury

b) wskaźnik natężenia

2. Dominanta
   

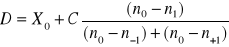
pozycja mediany

dla N nieparzystych

3. Kwartyle szeregów rozdzielczych przedziałowych:

;
;

4. Średnie klasyczne
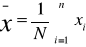
   , dla szeregu szczegółowego (wyliczającego)

, dla szeregu rozdzielczego punktowego

, dla szeregu rozdzielczego przedziałowego

a) suma odchyleń średniej arytmetycznej

b) średnia geometryczna
dla szeregu prostego

dla szeregu rozdzielczego

3. średnią chronologiczną
   

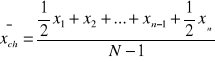
4. średnią harmoniczną
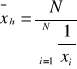
   dla szeregu szczegółowego

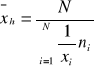
dla szeregu rozdzielczego punktowego

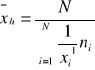
dla szeregu rozdzielczego wielowariantowego

5. POZYCYJNE MIARY ZMIANNOŚCI

1. odchylenie ćwiartkowe
   

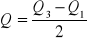
2. współczynnik zmienności
   

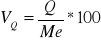
6. KLASYCZNE MIARY ZMIENNOŚCI (DYSPERSJI)

1. odchylenie przeciętne

• 
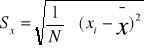
  dla szeregów prostych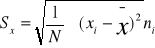

• 
  dla szeregów rozdzielczych punktowych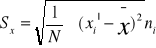

• 
  dla szeregów rozdzielczych przedziałowych

współczynnik zmienności :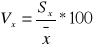

7. współczynniki koncentracji
   ,
   ,
   ,
   

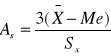
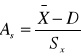
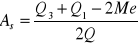
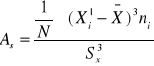
współczynnik koncentracji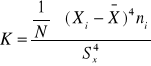
- k=3 dla rozkładu normalnego, k<3 dla rozkładu spłaszczonego

Do pomiaru nierównomierności podziału cechy w szeregu statystycznym wykorzystujemy współczynnik koncentracji Pearsona oraz krzywą Lorentza:

, gdzie
Fw_i i Fz_i - dystrybuanty empiryczne

k=0 rozkład równomierny, k=1 pełna koncentracja

8. Momenty centralne

- suma odchyleń od średniej arytmetycznej

- wariancja

- wykorzystywany do obliczeń współczynnika asymetrii

- wykorzystywany do obliczeń współczynnika koncentracji

momenty zwykłe

,
itd.

1. 
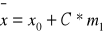
   - średni poziom badanej cechy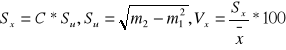

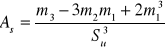
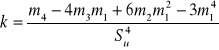
2. 
   

3. 
   

4. 
   

9. Rozkład dwumianowy:

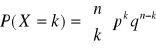
dla k całkowitych

• wartość oczekiwana (średnia) M.(X)=n*p

• wariancja D²(x)=n*p*q

• odchylenie standardowe
  

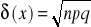
• współczynnik asymetrii
  
  

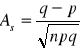
• współczynnik ekscesu (koncentracji)
  

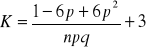
• dystrybuanta
  

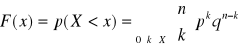
10. Estymator

Zgodny estymator limz'=z

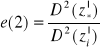
, D²=b²

11. Szacowanie średniej populacji na podstawie średniej z próby

1-a=0,90 to 2a=1,64

1-a=0,95 to 2a=1,96

1-a=0,99 to 2a=2,58

1. nieznane odchylenie standardowe populacji, duża próba (N>30)

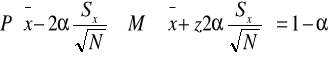
2. nieznane odchylenie standardowe populacji, mała próba (N<30)

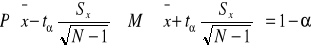
lub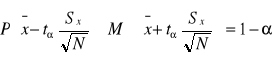

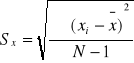
Ustalenia względnej precyzji szacunku danego parametru dokonujemy za pomocą następujących form:

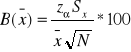
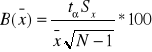
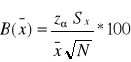
2. Szacowanie odchylenia standardowego populacji na podstawie próby

1. nieznane odchylenie standardowe, duża próba (N>30)

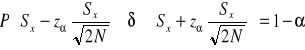
2. nieznane odchylenie standardowe, mała próba (N<30)

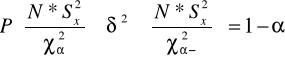
lub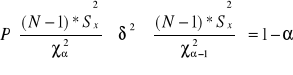

3. Szacowanie wskaźnika struktury (frakcji) populacji na podstawie próby - dokonujemy tylko gry N jest bardzo duże N>122.

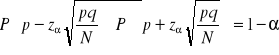
, gdzie

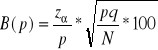
4. Ustalanie minimalnej liczebności próby: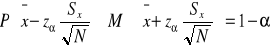

, gdzie d - zakładany błąd szacunku

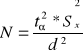
WERYFIKACJA

1. Test na zgodność średniej z próby ze średnią z populacji (zgodność średniej z populacji z wartością hipotetyczną):

1. N>30
   

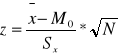
2. N<30
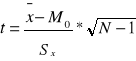
   lub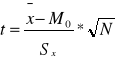
   

TEST DLA 2 ŚREDNICH

1. test na zgodność średnich z 2 populacji przy nieznanych odchyleniach standardowych populacji (N>30)

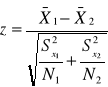
2. N<30

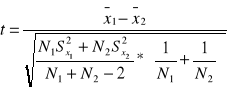
ta statystyka ma N₁+N₂-2 stopni swobody

3. 2 pomiary na tej samej próbie populacji Wyniki z próby losowej traktujemy jako różnicę pomiędzy parą obserwacji:

d_i=x_i-y_i

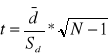
lub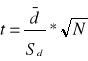

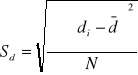
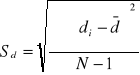
TEST ISTOTNOŚCI DLA WSKAŹNIKA STRUKTURY

,
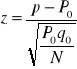
, P₀ - hipotetyczny wskaźnik struktury w populacji generalnej.

WERYFIKACJA HIPOTEZ STATYSTYCZNYCH TESTAMI NIEPARAMETRYCZNYMI

1. Test zgodności X² o postaci :

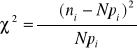
, gdzie pi - częstość teoretyczna (prawdopodobieństwo odpowiadające wartości podanej cechy w poszczególnym przedziale klasowym)

Uwaga! Test X2 ma tylko prawostronny obszar odrzucania!

2. Test X2 wykorzystany jako test niezależności :

,
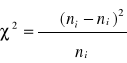
- liczebność teoretyczna

statystyka ta ma (k-1)(r-1)

TESTY ISTOTNOŚCI DLA WARIANCJI

• n<30

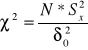
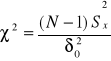
• n>30

TESTY WERYFIKUJĄCE HIPOTEZĘ O LOSOWOŚCI PRÓBY

Jeżeli x_i>Me a

X_i<Me b

X_i=Me pomijamy

---