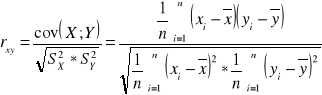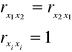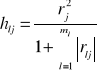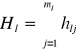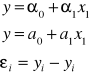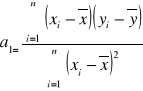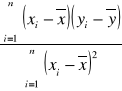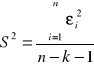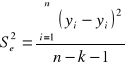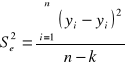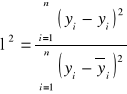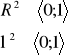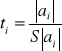Wzór	Opis
Kolokwium I
	Współczynnik korelacji Pearsona ( liniowy ) - zależność dodatnia - zależność ujemna - brak zależności lub - silna zależność liniowa
	Ogólna postać modelu ekonometrycznego
	Analiza macierzy współczynników korelacji - zależności
	Analiza macierzy współczynników korelacji - wzór na I eliminację zmiennych
	Analiza macierzy współczynników korelacji - wzór na 2 eliminację zmiennych
	Ilość możliwych kombinacji w metodzie współczynników informacyjnych Hellwiga m - ilość zmiennych objaśniających
	Metoda współczynników informacyjnych Hellwiga - wzór na wskaźnik indywidualny l - numer kombinacji j - numer zmiennej w badanej kombinacji ml - liczba zmiennych objaśniających w rozpatrywanej kombinacji
	Metoda współczynników informacyjnych Hellwiga - wzór na integralny pojemności informacyjnej
	Eliminacja zmiennych quasi-stałych Vi - współczynnik zmienności
	Eliminacja zmiennych quasi-stałych - wzór według którego eliminujemy zmienne z model
Kolokwium II
	Model ekonometryczny liniowy z jedną zmienną objaśniającą - postać ogólna
	Model ekonometryczny liniowy z jedną zmienną objaśniającą - wzór na a1
	Model ekonometryczny liniowy z jedną zmienną objaśniającą - wzór na a0
	Model liniowy ekonometryczny z jedną zmienną objaśniającą
=	Wzór na obliczanie parametru a1
	Wzór na obliczanie parametru a0
	Model ekonometryczny z więcej niż jedną zmienną objaśniającą
	Oceny modelu ekonometrycznego
	Oszacowanie parametrów strukturalnych
	Wariancja resztowa n - liczebność k - liczba zmiennych objaśniających - i-ta reszta S^2 - wariancja resztowa - odchylenie reszt
	Macierz odwrotna
	Wyznacznik macierzy Mij - minor odpowiadający elementowi ij, podwyznacznik macierzy A powstały przez skreślenie i-tego wiersza i j-tej kolumny
	Wyznaczanie reszty modelu
	Macierz wariancji i kowariancji parametrów strukturalnych modelu
	Weryfikacja modelu ekonometrycznego - wariancja resztowa k - liczba zmiennych objaśniających
	Weryfikacja modelu ekonometrycznego - wariancja resztowa k - liczba szacowanych parametrów
	Weryfikacja modelu ekonometrycznego - współczynnik zbieżności - współczynnik zbieżności określa jaka część całkowitej zmienności ( w procentach ) zmiennej objaśnianej nie została wyjaśniona przez dany model ekonometryczny ( przez zmienne objaśniające występujące w modelu ) Model ekonomiczny jest lepiej dopasowany do danych empirycznych jeżeli ℓ^2 jest bliższe zero
	Weryfikacja modelu ekonometrycznego - współczynnik determinacji - współczynnik determinacji określa jaka część całkowitej zmienności zmiennej objaśnianej została wyjaśniona przez dany model ekonometryczny ( przez zmienne objaśniające występujące w modelu ). Współczynnik determinacji jest odwrotnością współczynnika zbieżności Model ekonomiczny jest lepiej dopasowany do danych empirycznych jeżeli R^2 jest bliższe jedności
	Weryfikacja modelu ekonometrycznego - współczynnik zmienności losowej - odchylenie standardowe reszt o ile przeciętnie odchylają się wartości teoretyczne zmiennej objaśniającej od wartości empirycznych tych zmiennych Model ekonomiczny jest lepiej dopasowany do danych empirycznych jeżeli Se przyjmuje mniejszą wartość
	Zakres wartości i
	Badanie istotności parametrów strukturalnych modelu Jeżeli ti ≤ tα to nie ma podstaw do odrzucenia H0 - parametr ai jest nieistotny, a zmienna xi nieistotnie wpływa na zmienną objaśniającą i może zostać wyeliminowana z modelu Jeżeli ti > tα to H0 odrzucamy na rzecz H1 - parametr ai jest istotny, a zmienna xi istotnie wpływa na zmienną objaśniającą
	Weryfikacja hipotezy o istotności współczynnika korelacji wielorakiej R - współczynnik determinacji
Fα,m1=k;m2=n-k-1	Weryfikacja hipotezy o istotności współczynnika korelacji wielorakiej k - liczba zmiennych objaśniających n - liczebność F - statystyka Fishera Jeżeli F≤Fα to nie ma podstaw do odrzucenia H0. Współczynnik korelacji wielorakiej (R) jest nieistotny, a model jest źle dobrany do danych empirycznych Jeżeli F>Fα H0 odrzucamy na rzecz H1. Współczynnik korelacji wielorakiej (R) jest istotny, a model jest dobrze dopasowany do danych empirycznych. Jeżeli R^2 jest bliższe 1 - oznacza to dobre dopasowanie modelu
	Przedziały ufności
Kolokwium III

Ekonometria - wzory

- 5 -

---