WOJSKOWA AKADEMIA TECHNICZNA
LABORATORIUM FIZYCZNE
Grupa szkoleniowa: E5D9 Podgrupa: 1 Prowadzący: dr inż. Wiśniewski
Łukasz Madej Ocena z przygotowania Ocena końcowa:
Dawid Kruk do ćwiczeń:..................... ...........................
Sprawozdanie z Pracy Laboratoryjnej nr 21
Temat pracy: Badanie drgań relaksacyjnych
I. Wstęp teoretyczny
Drganiami relaksacyjnymi nazywamy drgania elektryczne, w których wzrosty i spadki napięcia zachodzą w sposób wykładniczy. Nie są to więc drgania harmoniczne. Zazwyczaj do ich wytwarzania stosuje się proces ładowania i rozładowywania kondensatora.
Zależności napięcia na okładkach kondensatora od czasu dana jest wzorem
podczas ładowania:

podczas rozładowywania:
Cykliczne przełączanie klucza w obwodzie tak, aby kondensator już to ładował się, już to rozładowywał wymusi powstanie w obwodzie drgań relaksacyjnych. (W ćwiczeniu funkcję klucza spełnia neonówka)
Okres drgań w tym ćwiczeniu laboratoryjnym dany jest wzorem:
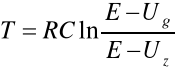
Uz - napięcie zapłonu neonówki;
Ug - napięcie gaśnięcia
Poprzez podłączanie różnych oporników i kondensatorów otrzymamy całą rodzinę drgań relaksacyjnych. Możliwe będzie także znalezienie pojemności nieznanego kondensatora.
Cel ćwiczenia:
Celem ćwiczenia jest zapoznanie się ze zjawiskiem drgań relaksacyjnych w obwodzie elektrycznym. W ramach zadania ma nastąpić wyznaczenie pojemności nieznanego kondensatora na podstawie uzyskanych wcześniej wyników ze znanymi kondensatorami.
II. Opracowanie wyników pomiarów
Tabela pomiarowa:
R [kΩ] |
C [nF] |
T1 [s] |
T2 [s] |
T3 [s] |
T4 [s] |
T5 [s] |
Tśr [s] |
500 |
5,6 |
6,497 |
6,700 |
6,492 |
6,409 |
6,495 |
6,519 |
|
8,2 |
7,477 |
7,995 |
7,576 |
7,576 |
7,503 |
7,625 |
|
10 |
8,030 |
8,174 |
8,198 |
8,334 |
8,201 |
8,187 |
|
14,7 |
11,351 |
11,435 |
11,296 |
11,540 |
11,170 |
11,358 |
|
15,8 |
11,632 |
11,632 |
11,637 |
11,739 |
11,733 |
11,675 |
|
17,3 |
13,0073 |
13,001 |
13,036 |
12,998 |
12,875 |
12,983 |
|
12,73 |
9,895 |
9,975 |
9,934 |
9,878 |
9,973 |
9,931 |
600 |
5,6 |
7,594 |
7,530 |
7,597 |
7,538 |
7,634 |
7,579 |
|
8,2 |
9,203 |
9,171 |
9,095 |
9,108 |
9,097 |
9,135 |
|
10 |
10,492 |
10,375 |
10,402 |
10,372 |
10,717 |
10,472 |
|
14,7 |
13,778 |
13,834 |
13,658 |
13,708 |
13,711 |
13,738 |
|
15,8 |
14,193 |
14,439 |
14,412 |
14,352 |
14,432 |
14,366 |
|
17,3 |
15,313 |
15,231 |
16,013 |
16,138 |
15,754 |
15,690 |
|
12,93 |
12,013 |
12,372 |
12,372 |
12,409 |
12,375 |
12,308 |
1. Obliczenia
1.1 Z użyciem rezystora R3
Obliczenie wartości średnich
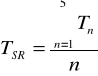
Wyniki zamieszczone w tabeli pomiarowej.
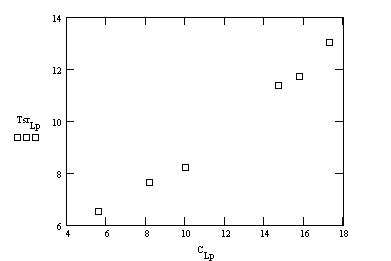
Wykres zależności T = f (C)
Obliczam współczynniki a oraz b metodą Gaussa najmniejszych kwadratów
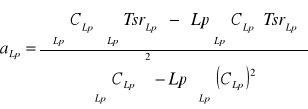
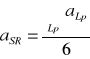
a śr = 0,87

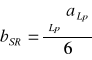
b śr = -1,18
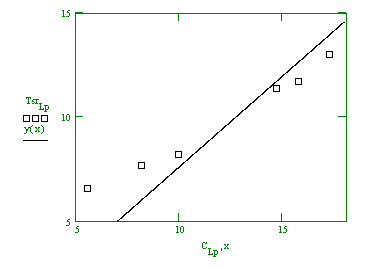
Wykres przedstawiający naniesione punkty eksperymentalne i doświadczalnie wyznaczoną prostą.
Obliczenie odchyleń standartowych σa oraz σ b
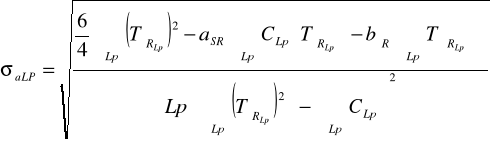
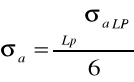
![]()
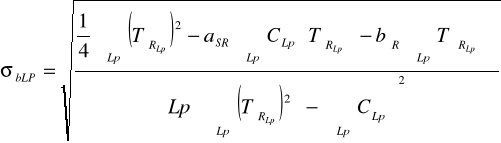

![]()
Obliczenia nieznanej pojemności CX
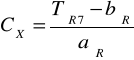
CX = 12,73 nF
Obliczenie średniego błędu kwadratowego σ TX
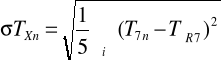
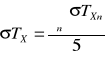
![]()
Obliczenie średniego błędu kwadratowego CX

![]()
Wyznaczenie przedziału ufności ΔCX
p = 0,98 p - zadany przedział ufności
![]()
ΔCX = 1,82
1.2 Z użyciem rezystora R4
Obliczenie wartości średnich
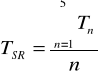
Wyniki zamieszczone w tabeli pomiarowej.
Wykres zależności T = f (C)
Obliczam współczynniki a oraz b metodą Gaussa najmniejszych kwadratów


a śr = 1,06
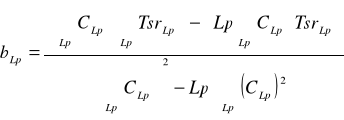

b śr = -1,38
Wykres przedstawiający naniesione punkty eksperymentalne i doświadczalnie wyznaczoną prostą.

Obliczenie odchyleń standartowych σa oraz σ b

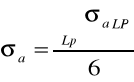
![]()
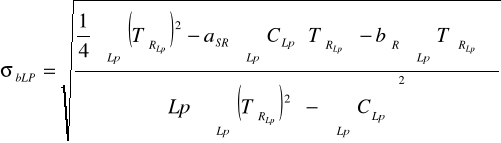

![]()
Obliczenia nieznanej pojemności CX

CX = 12,93 nF
Obliczenie średniego błędu kwadratowego σ TX


![]()
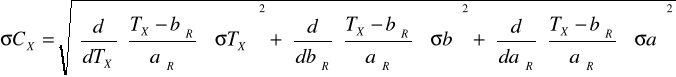
Obliczenie średniego błędu kwadratowego CX
![]()
Wyznaczenie przedziału ufności ΔCX
p = 0,98 p - zadany przedział ufności
![]()
ΔCX = 1,73 nF
Ri [kΩ] |
aŚr |
bŚr |
Cx [nF] |
σaśr |
σbśr |
σTx |
σCx [nF] |
p |
ΔCX [nF] |
R3 = 500 |
0,87 |
-1,18 |
12,73 |
0,09 |
1,15 |
0,03 |
1,86 |
0,98 |
1,82 |
R4 = 500 |
1,06 |
-1,38 |
12,93 |
0,10 |
1,31 |
0,13 |
1,77 |
0,98 |
1,73 |
III. Wnioski
Pomiary zostały przeprowadzone dla dwóch rezystancji 500kΩ i 600kΩ. Dla każdej pojemności kondensatora przeprowadzonych zostało pięć pomiarów okresów drgań. Czasy zamieszczone są w tabeli wyników pomiarów i podane są dla 1000 impulsów. Na ich podstawie przeprowadzone zostały obliczenia. Przeprowadzono pięć pomiarów czasu i na ich podstawie wyznaczono pojemność tego kondensatora (wynik zapisany w powyższej tabeli).
Z rysunków wynik, że dla wszystkich pojemności kondensatorów okresy drgań układają się na prostej. Na podstawie wykresów można stwierdzić, że wzrost rezystancji powoduje także wzrost okresu drgań, a co za tym idzie częstotliwość maleje ( f = 1/T ).
Myślę, że otrzymane wyniki są w pełni zadowalające. Znaleziona pojemność nieznanego kondensatora okazała dość się podobna dla obu serii pomiarów. Wynikające rozbieżności mieszczą się w dopuszczalnych granicach błędu.
Ćwiczenie w porównaniu z innymi było dość nudne i monotonne. Wkład studenta ograniczał się jedynie do powtórzeń tych samych czynności. Stąd można wyciągnąć wniosek, że mały udział studenta w doświadczeniu oraz duża liczba powtórzeń tego samego pomiaru sprawiają że takie rodzaje ćwiczeń są bardzo nie lubiane.
![]()
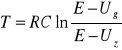
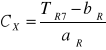

![]()
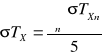
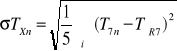
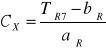
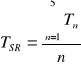
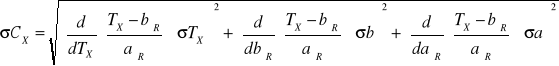
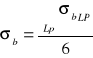

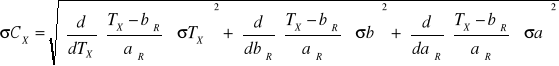
![]()
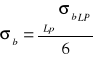
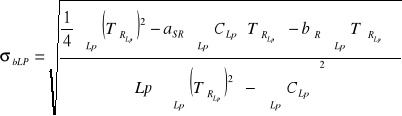
![]()

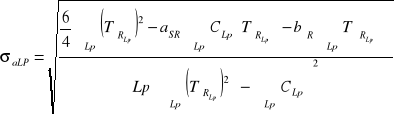
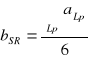
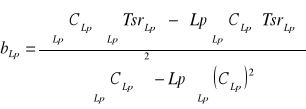
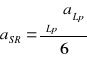
![]()
![]()
![]()

![]()
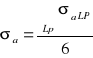
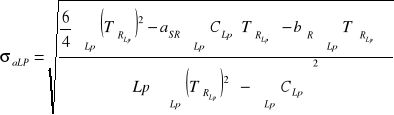




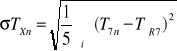

![]()
![]()
![]()
Wyszukiwarka