Zad. 1 (Num.Methods using Matlab, 7.1.1)

Rozważamy całkę oznaczoną funkcji f(x) w ustalonym przedziale [a, b] = [0, 1]. Dla obliczeń zastosuj wzory kwadratur:

a) punktu środkowego,

b) metody trapezów (2 węzły równoodległe),

c) metody Simpsona (3 węzły równoodległe),

d) metody 3/8 Simpsona (4 węzły równoodległe),

e) metody Boole'a (5 węzłów równoodległych),

Oszacuj błędy kwadratur numerycznych. Oblicz błędy porównując wartości kwadratur z obliczeniami analitycznymi.

Całkuj następujące funkcje:

a) f(x) = sin(πx)

b) f(x) = 1 + e^-xcos(4x)

c) f(x) = sin(√x)

Notatki metodyczne.

Celem jest utrwalenie podstawowych metod całkowania numerycznego, postaci błędu kwadratury oraz zrozumienie wymagań co do częstości próbkowania węzłami kwadratury x_k funkcji podcałkowej f(x).

Dla każdej z metod całkowania (kwadratury) należy:

1. naszkicować przedział całkowania, naszkicować położenie węzłów kwadratury, naszkicować przebieg funkcji podcałkowej zaznaczając jej wartości w węzłach kwadratury;

2. naszkicować w oparciu o wartości funkcji wyliczone w węzłach kwadratury przebieg wielomianu interpolacyjnego opartego na tych punktach; jak dobrze - czy źle - przybliża on funkcję podcałkową? Skąd taka jakość przybliżenia? Czy to wielomian interpolujący będzie podlegał całkowaniu w tej kwadraturze?

3. Wyliczyć wartość kwadratury (korzystając ze wzoru na kwadraturę) i wartość analityczną całki oznaczonej (użyć MATLABa do tej ostatniej operacji); ile wynosi błąd absolutny obliczenia całki przy pomocy kwadratury?

4. Używając oszacowania dla błędu kwadratury, wylicz wartość tego błędu; należy oszacować wielkość odpowiedniej pochodnej funkcji podcałkowej, wchodzącej do wyrażenia na błąd (wziąć kres górny lub dolny w przedziale całkowania); pomocnym będzie też zrobienie wykresu tej pochodnej i skomentowanie związku pomiędzy wykresem pochodnej a wielkością błędu kwadratury dla danej funkcji podcałkowej;

Zad. 2 (Num.Methods using Matlab, 7.1.4)

Scałkuj wielomian interpolacyjny Lagrange'a oparty na 2 węzłach x_o i x₁, a tym samym wyprowadź wzór na metodę trapezów dla obliczenia całki oznaczonej

Wyprowadź też wzór na oszacowanie błędu metody trapezów, korzystając ze wzoru na błąd E₁(x) w metodzie interpolacji wielomianem. Wielomian interpolacyjny Lagrange'a P₁(x) ma postać:

Notatki metodyczne.

Celem jest zapoznanie się z metodą wyznaczania wzorów na kwadraturę w oparciu o wielomian interpolacyjny.

1. Należy przypomnieć sobie metodę interpolacyjną Lagrange'a: funkcje bazowe oparte na węzłach interpolacji, sposób wykorzystania funkcji bazowych i wartości funkcji w węzłach interpolacji do stworzenia wielomianu interpolacyjnego; należy także przypomnieć sobie oszacowanie wielkości błędu interpolacji;

2. Jaką interpretację ma całkowanie wielomianu interpolującego oraz funkcji błędu?

3. Program w MATLABie, wyznaczający żądane wielkości ma postać:

wzor_kwadratury = 1/2*(f1+f0)*(x1-x0)

blad = -1/12*D2fDx2*(x1-x0)^3

Zad. 3 (Num.Methods using Matlab, 7.1.8)

Znając wzory na kwadratury numeryczne:

a) trapezów

b) Simpsona

dla przedziału całkowania [x₀, x₁], wyprowadź wzory na te kwadratury w innym przedziale [a, b]. Czy dokładność tych kwadratur uległa zmianie ?

Notatki metodyczne.

Typowe zadanie analityczne - odpowiadające na pytanie: jeśli określiliśmy wzory kwadratury dla jednego przedziału, to czy będą one obowiązywać także w innym przedziale ? Twierdząca odpowiedź umożliwia wyprowadzenie wzorów w dogodnym przedziale, a następnie użycie ich w innym przedziale.

1. Co odpowiada zamianie przedziału całkowania (jakie odwzorowanie?)

2. Jaka jest struktura wzorów odpowiedzialnych za dokładność całkowania? Czy zamiana zmiennych w całce coś zmieni?

Zad. 4 (Num.Methods using Matlab, 7.1.10)

Wyprowadź zamknięty wzór kwadratury Newtona-Cotesa, korzystając ze wzoru interpolacyjnego Newtona dla wielomianu P₅(x) stopnia 5, używając 6 równoodległych węzłów x_k = x₀ + kh, k=0,1,...,5. Podaj oszacowanie błędu tej kwadratury.

Wskazówki metodyczne.

Typowy przykład na obliczenia wzoru kwadratury. Celowym jest użycie symbolicznego pakietu MATLABa.

1. Należy wypisać wzór na wielomian interpolacyjny P₅(x) oparty o węzły interpolacji x_k; podstawowym będzie tutaj wyprowadzenie wzorów na współczynniki a_k w oparciu o różnice dzielone korzystające z wartości funkcji f(x_k); podobnie należy wyprowadzić wzór na błąd E₅(x);

2. Należy scałkować wielomian P₅(x) wyraz po wyrazie, i zebrać podobne wyrazy; ostatecznie, należy scałkować błąd E₅(x);

Otrzymuje się następujące wyniki (podanym niżej programem MATLABa):

Q₅(x) = 5/288*h*(19*f0+19*f5+75*f4+75*f1+50*f3+50*f2)

Błąd = -275/12096*D6fDx6*h^7

Zad. 5 (Hamming, 15.4.2)

Znajdź wzór kwadratury dla całki oznaczonej typu:

Jest to przykład kwadratury, w której całkowalna osobliwość (jądro całkowe K(x), w tym przypadku K(x) = ln(x)) jest włączona w wagi w_i kwadratury.

Oblicz wartość następujących całek i porównaj z wynikami obliczeń stosujących metodę Simpsona (raczej nie powinno dąć się wykonać takiego porównania - dlaczego ?):

a)

b)

c)

Przewodnik metodyczny.

Celem jest opanowanie metody współczynników nieoznaczonych (bezpośredniej) dla wyprowadzania wzorów kwadratów. Poważniejszym celem jest zrozumienie celu i metody włączenia jądra we współczynniki wagowe kwadratury w celu poprawienia (czy wręcz umożliwienia) całkowania numerycznego.

1. Przypomnij sobie zasadę wyprowadzenia wzoru kwadratury metodą bezpośrednią.

2. Czy podana kwadratura ma zadane węzły? Co jest szukane przy wyprowadzeniu wzoru?

3. Czy mamy do czynienia z całkowaniem klasy funkcji? Jakie jest jądro całkowalne K(x)? Jakie wartości i gdzie (dla jakich x_k) należy obliczyć przy obliczaniu wartości całki oznaczonej przy pomocy kwadratury?

4. Czy proponowana kwadratura jest typu otwartego czy zamkniętego? A kwadratura Simpsona oparta na tych samych węzłach? Jak wygląda wzór kwadratury Simpsona? Czy można go użyć do obliczeń podanej klasy funkcji podcałkowej?

5. Czy dla każdej funkcji f(x)ln(x) podana całka oznaczona będzie istniała?

6. Korzystając z funkcji ezplot() spróbuj naszkicować kilka funkcji typu f(x)*log(x) - czy całka oznaczona dla tych funkcji będzie istniała? Jak f(x) musi zachowywać się dla 0⁺ ?

7. Wyprowadź kwadraturę metodą bezpośrednią: napisz układ 3 równań, rozwiąż całki oznaczone, rozwiąż układ dla znalezienia współczynników wagowych kwadratury;

8. Dla każdego z podanych przykładów (a-c): naszkicuj funkcję f(x), f(x)*log(x); zaznacz węzły kwadratury na f(x); Jakiego pola szukamy (całka oznaczona)? Dla której z funkcji f(x) oczekujesz lepszych, a dla której gorszych wyników? Dlaczego? Jak wygląda błąd kwadratury? Od czego on zależy (jak dobrze wielomian P₂(x) interpoluje f(x)?)?

Wynik obliczenia wzoru kwadratury jest:

Stopień dokładności kwadratury jest N=2.

Poniższy program pokazuje, jak to zrealizować w MATLABie.

Należy zwrócić uwagę, jak MATLAB (jego pakiet symboliczny) został wykorzystany do:

1. ułożenia i rozwiązania układu równań metody bezpośredniej,

2. obliczenia stopnia dokładności kwadratury,

3. obliczeń wielomianów interpolujących,

4. sporządzenia interesujących wykresów pozwalających na analizę rozwiązań;

Zad. 6

Znajdź wzór kwadratury dla całki oznaczonej typu:

Jest to przykład kwadratury, w której całkowalna osobliwość (jądro całkowe K(x), w tym przypadku K(x)=√x) jest włączona w wagi kwadratury.

Oblicz wartości następujących całek i porównaj z wynikami obliczeń stosujących metodę 3/8 Simpsona (dlaczego błędy metody Simpsona są takie duże ?):

a)

b)

c)

Notatki metodyczne.

1. 
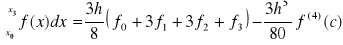
   Przypomnij sobie wzór metody 3/8 Simpsona (kwadratura Newtona-Cotesa, oparta na 4 węzłach odległych o h)

2. Wyprowadź wzór na podaną kwadraturę, stosując metodę bezpośrednią. Jaki jest powód, iż dążymy do włączenia funkcji K(x) = √x do wag w_i kwadratury? Dla podanych przypadków, jak wygląda funkcja podcałkowa K(x)*f(x) oraz jej 4-ta pochodna? Jaki będzie to miało wpływ na dokładność obliczeń? Gdzie jest sedno problemu (jak zachowuje się funkcja podcałkowa, a jak jej wielomian interpolujący P₃(x) - naszkicuj to) ?

3. Naszkicuj wielomian interpolujący P₃(x) dla każdej z funkcji f(x), nanieś na rysunki węzły interpolacji, naszkicuj f⁽⁴⁾(x) na tym samym wykresie. Jakie wnioski wyciągniesz co do dokładności opracowanej kwadratury?

4. Scałkuj analitycznie każdy z przykładów (jeśli to możliwe, możesz też użyć rozwinięcia f(x) w szereg Taylora w funkcji podcałkowej); scałkuj metodą 3/8 Simpsona oraz scałkuj opracowaną kwadraturą. Jak zmieniają się błędy?

Wyprowadzony wzór to:

Int(f; x₀, x₃) = 1/105*(4*f(0) + 18*f(1/3) + 36*f(2/3) + 12*f(1))

Ma on dokładność rzędu N=3.

Rozwiązanie zadania przedstawia następujący program:

% lab.4 zad6. plik: lab4_z6.m

% matoda bezposrednia dla kwadratury:

% I(K(x)f(x);0,1) = w0*f(0) + w1*f(1/3) + w2*f(2/3) + w3*f(1)

% szukamy dla ogolnego przypadku wezlow w odleglosci h

% przypadki K(x): P(x), sin(pi*x), tan(x)

syms x h f0 f1 f2 f3 x0 x1 x2 x3

% dla wielomianu: f=1, f=x, f=x^2, f=x^3, sprawdzenie dla f=x^4

% prawe strony

b0 = int(x^(1/2)*1, 0, 3*h);

b1 = int(x^(1/2)*x, 0, 3*h);

b2 = int(x^(1/2)*x^2, 0, 3*h);

b3 = int(x^(1/2)*x^3, 0, 3*h);

B = [b0; b1; b2; b3];

% macierz ukladu rownan

A = sym([...

1, 1, 1, 1;

0*h, h, 2*h, 3*h;

(0*h)^2, h^2, (2*h)^2, (3*h)^2;

(0*h)^3, h^3, (2*h)^3, (3*h)^3]);

W = A\B

% ogolny wzor kwadratury

IKW = [f0 f1 f2 f3]*W; IKW = simple(IKW);

disp('Ogolny wzor kwadratury: '), pretty(IKW)

% sprawdzenie dla int(x^0.5, 0, 3h), f(x)=1

I = sym([1 1 1 1])*W, b0

if (I == b0), disp('Kwadratura zgodna z wynikiem analitycznym'), end

% Nasz konkretny wzor dla h=1/3

h = sym(1/3);

W = subs(W), disp('Wzor kwadratury jest: '), KW = [f0,f1,f2,f3]*W

% mozna go zapisac: KW = 1/105*(4f0 + 18f1 + 36f2 + 12f3)

% sprawdzenie dokladnosci kwadratury

b4 = int(x^(1/2)*x^4, 0, 1), I4KW = [0, 1/3, 2/3, 1].^4 * W, E4 = b4-I4KW

if (E4), disp('Stopien dokladnosci N=3'), end

close all

% rozwiazanie dla I=int(sin(pi*x)*x^0.5, 0,1)

% wykres funkcji podcalkowej i jej 4-tej pochodnej

K = x^(1/2); f = sin(pi*x); F = K*f;

figure(1), ezplot(F,[0,1]), legend('Funkcja podcalkowa Kf')

figure(2), ezplot(diff(F,4), [0,1]), legend('Czwarta pochodna Kf')

% wielomian interpolujacy

x0 = 0; x1 = 1/3; x2 = 2/3; x3 = 1;

% TABLICA ROZNIC DZIELONYCH DLA K(x)*f(x)

F0 = [sin(pi*x0), sin(pi*x1), sin(pi*x2), sin(pi*x3)].*([x0, x1, x2, x3].^(1/2));

F1 = 1/(1*h)*[F0(2)-F0(1), F0(3)-F0(2), F0(4)-F0(3)];

F2 = 1/(2*h)*[F1(2)-F1(1), F1(3)-F1(2)];

F3 = 1/(3*h)*[F2(2)-F2(1)];

P1 = F0(1) + F1(1)*(x-x0);

P2 = P1 + F2(1)*(x-x0)*(x-x1);

P3 = P2 + F3(1)*(x-x0)*(x-x1)*(x-x2);

% wykres roznicy wielomianu interpolujacego K*f i samej K*f

figure(3), ezplot(F-P3,[0,1]), legend('Roznica f.podcalk.K(x)f(x) i jej wielom.interp.P3')

% teraz tylko dla funkcji f(x) - reszte zalatwia wagi

% TABLICA ROZNIC DZIELONYCH DLA f(x)

F0 = [sin(pi*x0), sin(pi*x1), sin(pi*x2), sin(pi*x3)];

F1 = 1/(1*h)*[F0(2)-F0(1), F0(3)-F0(2), F0(4)-F0(3)];

F2 = 1/(2*h)*[F1(2)-F1(1), F1(3)-F1(2)];

F3 = 1/(3*h)*[F2(2)-F2(1)];

P1 = F0(1) + F1(1)*(x-x0);

P2 = P1 + F2(1)*(x-x0)*(x-x1);

P3 = P2 + F3(1)*(x-x0)*(x-x1)*(x-x2);

% wykres roznicy wielomianu interpolujacego f i samej f

figure(4), ezplot(f-P3,[0,1]), legend('Roznica f.podcalk f(x). i jej wielom.interp.P3')

% obliczenie wartosci calki 3 metodami

IAnalit = int(x^(1/2)*taylor(sin(pi*x),15), 0, 1), IAnalit = eval(IAnalit)

ff0 = [sin(pi*x0), sin(pi*x1), sin(pi*x2), sin(pi*x3)].*([x0, x1, x2, x3].^(1/2));

ISimps38 = 3*h/8*(ff0(1)+3*ff0(2)+3*ff0(3)+ff0(4)), ISimps38=eval(ISimps38)

IKwadr = F0*W, IKwadr = eval(IKwadr)

disp('Bledy absolutne kwadratur')

RS = IAnalit - ISimps38, RK = IAnalit - IKwadr

% to samo dla funkcji f(x)=tan(x)

% rozwiazanie dla I=int(tan(x)*x^0.5, 0,1)

% wykres funkcji podcalkowej i jej 4-tej pochodnej

K = x^(1/2); f = tan(x); F = K*f;

figure(5), ezplot(F,[0,1]), legend('Funkcja podcalkowa Kf')

figure(6), ezplot(diff(F,4), [0,1]), legend('Czwarta pochodna Kf')

% wielomian interpolujacy

x0 = 0; x1 = 1/3; x2 = 2/3; x3 = 1;

% TABLICA ROZNIC DZIELONYCH DLA K(x)*f(x)

F0 = [tan(x0), tan(x1), tan(x2), tan(x3)].*([x0, x1, x2, x3].^(1/2));

F1 = 1/(1*h)*[F0(2)-F0(1), F0(3)-F0(2), F0(4)-F0(3)];

F2 = 1/(2*h)*[F1(2)-F1(1), F1(3)-F1(2)];

F3 = 1/(3*h)*[F2(2)-F2(1)];

P1 = F0(1) + F1(1)*(x-x0);

P2 = P1 + F2(1)*(x-x0)*(x-x1);

P3 = P2 + F3(1)*(x-x0)*(x-x1)*(x-x2);

% wykres roznicy wielomianu interpolujacego K*f i samej K*f

figure(7), ezplot(F-P3,[0,1]), legend('Roznica f.podcalk.K(x)f(x) i jej wielom.interp.P3')

% teraz tylko dla funkcji f(x) - reszte zalatwia wagi

% TABLICA ROZNIC DZIELONYCH DLA f(x)

F0 = [tan(x0), tan(x1), tan(x2), tan(x3)];

F1 = 1/(1*h)*[F0(2)-F0(1), F0(3)-F0(2), F0(4)-F0(3)];

F2 = 1/(2*h)*[F1(2)-F1(1), F1(3)-F1(2)];

F3 = 1/(3*h)*[F2(2)-F2(1)];

P1 = F0(1) + F1(1)*(x-x0);

P2 = P1 + F2(1)*(x-x0)*(x-x1);

P3 = P2 + F3(1)*(x-x0)*(x-x1)*(x-x2);

% wykres roznicy wielomianu interpolujacego f i samej f

figure(8), ezplot(f-P3,[0,1]), legend('Roznica f.podcalk f(x). i jej wielom.interp.P3')

% obliczenie wartosci calki 3 metodami

IAnalit = int(x^(1/2)*taylor(tan(x),15), 0, 1), IAnalit = eval(IAnalit)

ff0 = [tan(x0), tan(x1), tan(x2), tan(x3)].*([x0, x1, x2, x3].^(1/2));

ISimps38 = 3*h/8*(ff0(1)+3*ff0(2)+3*ff0(3)+ff0(4)), ISimps38=eval(ISimps38)

IKwadr = F0*W, IKwadr = eval(IKwadr)

disp('Bledy absolutne kwadratur')

RS = IAnalit - ISimps38, RK = IAnalit - IKwadr

Metody Numeryczne - Zajęcia 4 - Zadania do rozwiązania na laboratorium

DOC: zad-lab-4-przewodnik Strona 2 z 8

syms x x0 x1 f0 f1 N D2fDx2

L10 = (x-x1)/(x0-x1);

L11 = (x-x0)/(x1-x0);

P1 = L10*f0 + L11*f1;

wzor_kwadratury = int(P1, x0, x1);

wzor_kwadratury = simple(wzor_kwadratury);

N=1;

E1 = (x-x0)*(x-x1)*D2fDx2/(N*(N+1));

blad = int(E1, x0, x1);

blad = simple(blad);

% lab4. zad 4

syms x0 k h f0 f1 f2 f3 f4 f5 D6fDx6

% tablica roznic dzielonych

F0 = [f0, f1, f2, f3, f4, f5];

F1 = 1/(1*h)*[F0(2)-F0(1), F0(3)-F0(2), F0(4)-F0(3),F0(5)-F0(4), F0(6)-F0(5)];

F2 = 1/(2*h)*[F1(2)-F1(1), F1(3)-F1(2), F1(4)-F1(3),F1(5)-F1(4)];

F3 = 1/(3*h)*[F2(2)-F2(1), F2(3)-F2(2), F2(4)-F2(3)];

F4 = 1/(4*h)*[F3(2)-F3(1), F3(3)-F3(2)];

F5 = 1/(5*h)*[F4(2)-F4(1)];

% wspolczynniki

a0 = F0(1); a0 = simple(a0);

a1 = F1(1); a1 = simple(a1);

a2 = F2(1); a2 = simple(a2);

a3 = F3(1); a3 = simple(a3);

a4 = F4(1); a4 = simple(a4);

a5 = F5(1); a5 = simple(a5);

% wielomiany interpolacyjne

P0 = a0; P1 = P0 + a1*(x-x0); P2=P1+a2*(x-x0)*(x-x0-h);

P3 = P2 + a3*(x-x0)*(x-x0-h)*(x-x0-2*h);

P4 = P3 + a4*(x-x0)*(x-x0-h)*(x-x0-2*h)*(x-x0-3*h);

P5 = P4 + a5*(x-x0)*(x-x0-h)*(x-x0-2*h)*(x-x0-3*h)*(x-x0-4*h);

P5=simplify(P5);

% kwadratura

wzor = int(P5, x0, x0+5*h); wzor = simple(wzor), pretty(wzor)

% blad

E6 = (x-x0)*(x-x0-h)*(x-x0-2*h)*(x-x0-3*h)*(x-x0-4*h)*(x-x0-5*h)*D6fDx6/(6*5*4*3*2);

E6int = int(E6,x0,x0+5*h); E6int=simple(E6int), pretty(E6int)

% lab4. zad5, plik lab4_z5.m

% wyprowadzenie wzoru na kwadrature:

%

% -int(f(x)*log(x), 0, 1) = w0*f(0) + w1*f(1/2) + w2*f(1)

%

syms x f0 f1 f2 D3fDx3 h x0 x1 x2

% wyrazy wolne dla metody bezposredniej

% f=1, f=x, f=x^2

a0 = -int(1*log(x),0,1);

a1 = -int(x*log(x),0,1);

a2 = -int(x^2*log(x),0,1);

B = [a0;a1;a2];

% macierz wspolczynnikow

A = sym( ...

[ 1, 1, 1; ...

0, 1/2, 1; ...

0, (1/2)^2, (1)^2]);

% rozwiązanie

W = A\B % macierz (wektor) wspolczynnikow

w0 = W(1), w1 = W(2), w2 = W(3)

% obliczenie rzedu dokladnosci funkcji - dla f=x^3

I3 = -int(x^3*log(x),0,1)

IKw3 = w0*0^3 + w1*(1/2)^3 + w2*(1)^3

E3 = I3 - IKw3

if (E3), disp('E3 rozne od zera, wiec dokladnosc kwadratury N=2'), end

blad = E3/(3*2*1)*h^3*D3fDx3

% przyklady obliczen kwadratury dla roznych funkcji

% a) sin(x)*log(x)

% b) x^(3/2)*log(x)

disp('Obliczenia dla (a): sin(x)*log(x)')

a=1.0e-10; b=1;

Ia_teoret = -int(sin(x)*log(x), a, b), ITeoret=eval(Ia_teoret)

% wykres funkcji podcalkowej

close all

figure(1)

ezplot(sin(x)*log(x), [0,1]), title('funkcja podcalkowa = K(x)*sin(x), K(x)=log(x)')

% wykres wielomianu interpolujacego f(x)

x0 = sym(0); x1 = sym(1/2); x2= sym(1);

F0 = [sin(x0), sin(x1), sin(x2)];

F1 = 1/(1/2)*[F0(2)-F0(1), F0(3)-F0(2)];

F2 = 1/1*[F1(2)-F1(1)];

P2 = F0(1) + F1(1)*(x-x0) + F2(1)*(x-x0)*(x-x1);

figure(2)

ezplot(sin(x),[0,1]), hold on

ezplot(P2, [0,1])

plot([eval(x0),eval(x1),eval(x2)], eval(F0), 'o')

title('wykres funkcji f(x)=sin(x) i jej wielomianu interpolujacego P2(x)')

legend('f(x)=sin(x)', 'P2(x)', 'o - wezly interpolacji')

% obliczenia numeryczne

Ia_numer = F0*W, INumer = eval(Ia_numer)

Ra = INumer - ITeoret

% teraz obliczenia dla drugiej funkcji f(x)*K(x) = x^(3/2)*log(x)

disp('Obliczenia dla (b): x^(3/2)*log(x)')

a=0; b=1;

Ib_teoret = -int(x^(3/2)*log(x), a, b), ITeoret=eval(Ib_teoret)

% wykres funkcji podcalkowej

figure(3)

ezplot(x^(3/2)*log(x), [0,1]), title('funkcja podcalkowa = K(x)*x''^(3/2), K(x)=log(x)')

% wykres wielomianu interpolujacego f(x)

x0 = sym(0); x1 = sym(1/2); x2= sym(1);

F0 = [ x0^(3/2), x1^(3/2), x2^(3/2)];

F1 = 1/(1/2)*[F0(2)-F0(1), F0(3)-F0(2)];

F2 = 1/1*[F1(2)-F1(1)];

P2 = F0(1) + F1(1)*(x-x0) + F2(1)*(x-x0)*(x-x1);

figure(4)

ezplot(x^(3/2),[0,1]), hold on

ezplot(P2, [0,1])

plot([eval(x0),eval(x1),eval(x2)], eval(F0), 'o')

title('wykres funkcji f(x)=(x)''^(3/2) i jej wielomianu interpolujacego P2(x)')

legend('f(x)=(x)^(3/2)', 'P2(x)', 'o - wezly interpolacji')

% obliczenia numeryczne

Ib_numer = F0*W, INumer = eval(Ib_numer)

Rb = INumer - ITeoret

---