Nr ćwicz. 108	Data: 14.01.98	Arkadiusz Sitek	Wydział Elektryczny	Semestr: I	Grupa: T4
prowadzący: prof. dr hab. Danuta Wróbel					Przygotowanie:	Wykonanie:	Ocena ostat.:

Temat: Wyznaczanie modułu Younga metodą ugięcia.

Wstęp teoretyczny:

Gdy na pręt podłużny działa siła prostopadle do jego długości, doznaje on ugięcia, a wielkość tzw. strzałki ugięcia S (rys. 1.) jest zawsze proporcjonalna do siły F, a także zależy od wymiarów geometrycznych, sposobu mocowania pręta i rodzaju materiału z którego jest on wykonany.

Rys. 2. Element pręta zgiętego

Rys. 1. Ugięcie pręta

Zgodnie z prawem Hooke'a wydłużenie jest proporcjonalne do siły i długości początkowej oraz odwrotnie proporcjonalne do powierzchni przekroju

gdzie: E - moduł Younga,
- siła rozciągająca badaną warstwę elementarną.

Taka sama siła, lecz przeciwnie skierowana, działa na warstwę elementarną położoną symetrycznie poniżej warstwy neutralnej N. Moment siły
względem warstwy N wynosi

Całkowity moment M sił działających na wszystkie warstwy zawarte między przekrojami 1 i 2 obliczam całkując powyższe równanie względem y po całej grubości

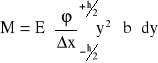
(1)

Jeśli oznaczę

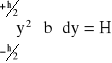
(2)

to równanie (1) mogę napisać w postaci

(3)

Równanie to otrzymałem rozpatrując odkształcenie pręta, którego bezpośrednią przyczyną jest siła F przyłożona do jego końca. Moment tej siły względem przekroju 2 wynosi
lub zaniedbując wielkość
jako małą w porównaniu z x

(4)

Kąt
jest zawarty między stycznymi do pręta w punktach, gdzie przekroje 1 i 2 przecinają górną powierzchnię. Na podstawie rysunku mogę napisać następujący związek

Wstawiając powyższe równanie do wzoru (3) i porównując wzory (3) i (4) otrzymuję elementarną strzałkę ugięcia

Całkowitą strzałkę ugięcia otrzymuję całkując powyższe równanie po całej długości pręta

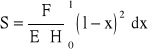
Po scałkowaniu, wyrażenie na całkowitą strzałkę ugięcia przyjmuje postać

Wartość współczynnika H zależy od kształtu i rozmiarów geometrycznych pręta. Gdy przekrój jest prostokątem o wysokości h i szerokości b, to całkowanie równania (2) prowadzi do wyniku

Całkowanie podobnego wyrażenia dla przekroju kołowego daje

Podstawiając wartości współczynników H otrzymuję odpowiednio dla obu przekrojów strzałki ugięcia

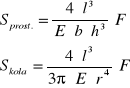
Otrzymane powyżej wzory odnoszą się do pręta jednostronnie obciążonego i jednym końcem umocowanego. Równania te można łatwo dostosować do sytuacji, gdy pręt jest swobodnie oparty dwoma końcami i obciążony w środku. Zachowuje się on wtedy tak, jak gdyby był zamocowany w środku, a na jego końce działały siły
skierowane ku górze. Siła
działa wtedy na pręt o długości
.

Po uwzględnieniu tych warunków w poprzednich wzorach uzyskuję wzory na strzałki ugięcia prętów

Rys. 3. Ugięcie pręta

dwustronnie podpartych

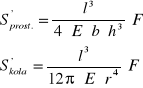
Z powyższych wzorów obliczam moduł Younga dla przekroju prostokątnego:

(5)

i dla przekroju kołowego:

(6)

Tabela pomiarowa:

Lp.	obciążenie [g]	wysokość h [mm]	strzałka s [mm]
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
14.
15.
16.
17.

Lp.	obciążenie [g]	wysokość h [mm]	strzałka s [mm]
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
14.
15.
16.
17.

Analiza pomiarów:

Pręt o przekroju kwadratowym:

Lp.	m [g]	h przy ros. obc. [mm]	h przy mal. obc. [mm]	h średnie [mm]	strzałka DS [mm]
1.	200	614,6	614,7	614,65	0,35
2.	400	614,25	614,3	614,27	0,73
3.	900	613,1	613,2	613,15	1,85
4.	1400	611,8	611,85	611,87	3,13
5.	1900	610,7	610,7	610,7	4,3

Pręt o przekroju kołowym:

Lp.	m [g]	h przy ros. obc. [mm]	h przy mal. obc. [mm]	h średnie [mm]	strzałka DS [mm]
1.	200	614,45	614,35	614,4	0,6
2.	400	613,8	613,7	613,75	1,25
3.	900	612,4	612,3	612,35	2,65
4.	1400	610,8	610,8	610,8	4,2
5.	1900	609,35	609,35	609,35	5,65

Lp.	m [g]	F [N]	DS [mm]	E [N/m^2]	DE [N/m^2]
pręt o przekroju prostokątnym
1.	200	1,962	0,35	9,88	5,9
2.	400	3,924	0,73	9,47	2,9
3.	900	8,829	1,85	8,41	1,2
4.	1400	13,734	3,13	7,73	0,7
5.	1900	18,639	4,3	7,64	0,6
pręt o przekroju kołowym
1.	200	1,962	0,6	9,79	3,8
2.	400	3,924	1,25	9,4	2
3.	900	8,829	2,65	9,97	1,3
4.	1400	13,734	4,2	9,79	1
5.	1900	18,639	5,65	9,88	0,9

Obliczenia:

W celu obliczenia moduły Younga korzystam ze wzorów (5) i (6):

Siłę uginającą pręt wyznaczam ze wzoru:

Przykładowe obliczenia dla pręta prostokątnego pomiar nr 1:

Rachunek błędu:

Błąd wyznaczenia modułu Younga dla pręta o przekroju prostokątnym liczony metodą różniczki logarytmicznej:

Błąd wyznaczenia modułu Younga dla pręta o przekroju kołowym liczony metodą różniczki logarytmicznej:

Wynik końcowy:

Dla pręta o przekroju prostokątnym (aluminium):

Dla pręta o przekroju kołowym (miedź):

Wnioski:

Badany pręt o przekroju prostokątnym wykonany był z aluminium. Otrzymana wartość modułu Younga zgadza się w granicach błędu z wartością tablicową która wynosi .

Pręt o przekroju kołowym wykonany był z miedzi. Wartość tablicowa modułu Younga dla miedzi wynosi co zgadza się z uzyskanym wynikiem.

Im mniejsza wartość moduły Younga tym większemu odkształceniu ulega ciało pod wpływem działającej siły (np. miękka guma posiada moduł Younga równy zaledwie ).

Jak wynika z wykresu bardzo duży wpływ na ugięcie ma również przekrój pręta. Pomimo iż moduł Younga dla pręta o przekroju prostokątnym jest mniejszy niż tego o przekroju kołowym, ulega on mniejszemu ugięciu.

---