IV.1.Siły przekrojowe w prętowych ustrojach statycznie wyznaczalnych.

Definicje:

Pręt - bryła, której jeden wymiar (długość) jest nieporównywalnie duży w stosunku do pozostałych.

Oś pręta - miejsce geometryczne punktów, będących środkami ciężkości przekrojów pręta dowolnymi płaszczyznami przecinającymi jego tworzące

Przekrój poprzeczny pręta - przekrój płaszczyzną prostopadłą do osi pręta

Układ statycznie wyznaczalny - układ, dla którego można jednoznacznie wyznaczyć reakcje na podstawie równań równowagi sił =>

• liczba reakcji równa jest liczbie niezależnych równań równowagi

• liczba stopni swobody zapewniających geometryczną niezmienność układu równa się 0

Układ statycznie niewyznaczalny - układ, dla którego z równań równowagi otrzymuje się nieskończenie wiele rozwiązań na siły reakcji =>

• liczba reakcji jest większa od liczby niezależnych równań równowagi

• liczba stopni swobody zapewniających geometryczną niezmienność układu równa się 0

Układ chwiejny - układ, dla którego równania równowagi stanowią sprzeczny układ algebraicznych równań

• liczba reakcji jest mniejsza od liczby niezależnych równań równowagi

• liczba stopni swobody jest większa od 0

Siły przekrojowe

Założenia:

1. Założenie o continuum materialnym - każdy punkt geometryczny ciała ma przypisaną masę, która jest w sposób ciągły rozłożona w objętości konstrukcji.

2. Założenie o równowadze statycznej - zdolność powracania ustroju do położenia równowagi, z którego został wyprowadzony przez działanie dowolnej przyczyny.

3. Zasada zesztywnienia - wpływ przemieszczeń na obliczanie reakcji i sił wewnętrznych jest pomijalnie mały.

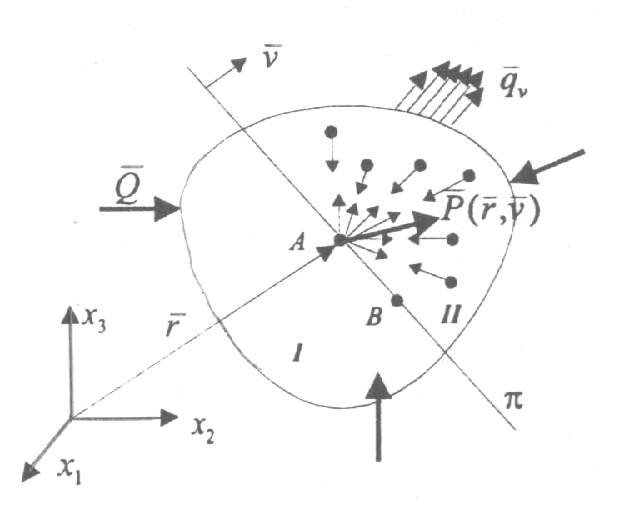
Weźmy pod uwagę bryłę sztywną pozostającą w równowadze statecznej, poddaną oddziaływaniu pewnego układu sił zewnętrznych

Wewnątrz wybieramy dowolny punkt A i prowadzimy przez niego płaszczyznę π o wersorze normalnym ν, która dzieli naszą bryłę na dwie części I i II. Przyjmujemy, że punkt A należy do I. Na punkt A działa pęk wektorów sił z jakimi wszystkie punkty materialne części II oddziałują na niego. Tworzą one zbieżny układ sił, którego suma stanowi wypadkową tego układu zaczepioną w punkcie A - to jest właśnie owa siła wewnętrzna. Siła ta jest funkcją :

• Położenia punktu - bo gdy inny punkt to inne siły

• Wektora normalnego płaszczyzny podziału

Siła wewnętrzna - funkcja wektorowa określająca wypadkową sił międzycząsteczkowych.

I tu pada pytanie jak ją wyznaczyć ? Skorzystamy z następujących twierdzeń:

Twierdzenie 1 ( o układach sił wewnętrznych i zewnętrznych ):

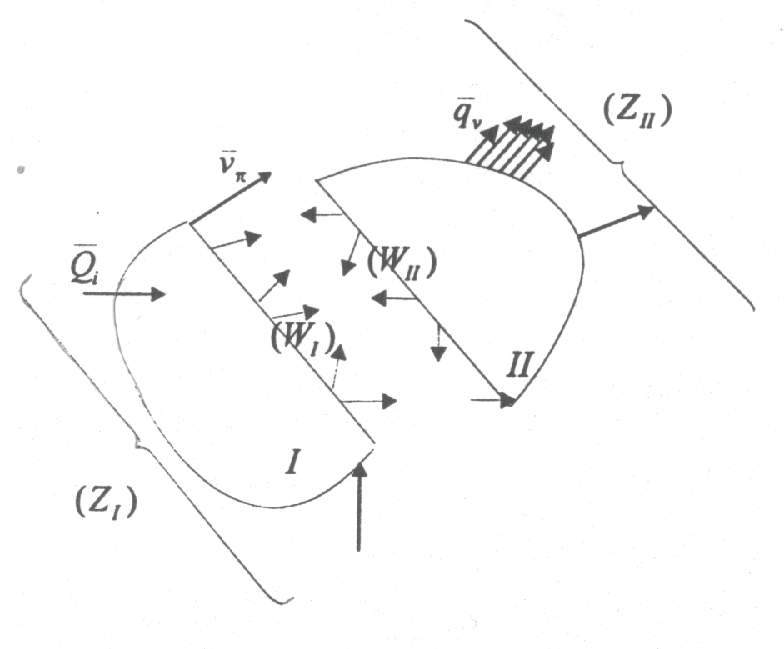
Układ sił wewnętrznych przyłożonych do części I jest równoważny układowi sił zewnętrznych przyłożonych do części II

Twierdzenie 2 ( o układach równoważnych ):

Jeżeli dwa układy są równoważne to :

• Sumy obu układów są sobie równe

• Momenty liczone względem tego samego punktu są równe

⇒
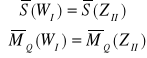
jest to układ zredukowany w punkcie Q

Stąd otrzymujemy siły wewnętrzne w konstrukcjach prętowych

W konstrukcjach prętowych układ zredukowany sił wewnętrznych odnosić się będzie do przekroju poprzecznego pręta, ze środkiem redukcji w środku ciężkości przekroju poprzecznego.

Układ zewnętrzny może zredukować się w szczególnych przypadkach do :

1. Wypadkowej prostopadłej do przekroju poprzecznego pręta - siła podłużna ( osiowa, normalna ) N

2. Wypadkowej leżącej w płaszczyźnie przekroju poprzecznego - siła poprzeczna ( tnąca, ścinająca ) Q

3. Pary sił leżących w płaszczyźnie przekroju - moment skręcający

4. Pary sił w płaszczyźnie prostopadłej do płaszczyzny przekroju - moment zginający

Przypomnieć sobie jeszcze należałoby jakie znamy układy prętowe płaskie i przestrzenne. Metody rozwiązywania danego układu, twierdzenia dotyczące danych układów ( np. kratownic )

---