Wyznaczanie podstawowych parametrów ruchu punktu. Metoda 1
ϕP, λP - odpowiednio: szerokość i długość geograficzna punktu P na płycie ............
ϕX , λX - odpowiednio: szerokość i długość geograficzna bieguna obrotu płyty..............
v - wektor prędkości X na płycie, jest prostopadły do XP
R - promień Ziemi 6371 km
ω - prędkość kątowa wokół bieguna P
a - odległość kątowa między biegunem obrotu a punktem X
cosa = cosb⋅cosc + sinb ⋅sinc⋅cosA
b = 90 - ϕX c = 90 - ϕP A = λP - λX
v - prędkość płyty (wartość wektora):
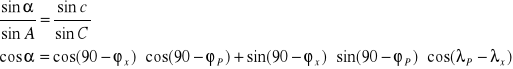
![]()
![]()
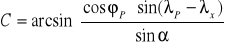
Wynik: ν = ………………………… β = …………………………
Uwagi:
1. Proszę pamiętać o znakach przy wartościach wprowadzanych współrzędnych:
ujemne wartości dla szerokości geograficznej południowej i długości geograficznej zachodniej.
2. Bok trójkąta sferycznego nie może mieć wartości ujemnej.
3. W wyznaczaniu prędkości liniowej konieczne jest stosowanie miary kątowej w radianach.
Wyznaczenie pełnej informacji o wektorze ruchu płyt. Metoda 2:
DANE:
Dysponujemy informacją o położeniu danego punktu i bieguna rotacji E:
ϕP, λP -odpowiednio: szerokość i długość geograficzna bieguna obrotu płyty ……….
ϕX, λX - odpowiednio: szerokość i długość geograficzna punktu P na płycie…………
R - promień Ziemi = 6371 km
![]()
(lub ω) to wektor prędkości (kątowej) rotacji płyt .………………………. [°/mln lat]
to pozycja wektora analizowanego punktu P,
Należy wyznaczyć wektor prędkości liniowej
![]()
![]()
Etapy obliczeń:
1. Proszę przeliczyć wszystkie wartości kątowe [°] na radiany.
2. Przeliczamy położenia współrzędne wektorów na układ kartezjański:
Px = cosϕ ∙ cosλ
Py = cosϕ ∙ sinλ
Pz = sinϕ
Oraz:
Ex = cosϕ ∙ cosλ
Ey = cosϕ ∙ sinλ
Ez = sinϕ
Należy pamiętać o znakach: ujemne wartości dla szerokości geograficznej południowej i długości geograficznej zachodniej.
3. Obliczamy składowe wektora prędkości kątowej (radiany!):
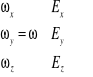
4.Następnie obliczmy iloczyn wektorowy, co pozwala wyznaczyć składowe wektora prędkości w układzie kartezjańskim:
![]()
5. Ostatni etap: przeliczenie współrzędnych wektora na układ współrzędnych płaskich:
,
gdzie:
T=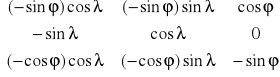
6. Ostateczny wynik: ze składowych wektora prędkości w lokalnym układzie współrzędnych wyznaczamy wartości wektora w kierunku określonym przez azymut. Uzyskujemy wartość wektora:
![]()
oraz jego azymut, azymut ruchu: 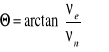
Wynik .................................................................................
Wyniki ze stacji EPN
Proszę podać parametry ruchu dla swojej stacji azymut oraz vx, vy, vz (składowe wektora
w dowolnym układzie systemu ITRS a nie ETRS!). Informacje w serwisie:
Składowe są podane w układzie geocentrycznym należy je przetransformować do układu topocentrycznego (podobnie jak w poprzednim zadaniu) i podać wyniki: vn, ve,vd.
Proszę zrobić zestawienie:
Zestawienie wyników
Metoda |
azymut wektora prędkości |
wartość wektora prędkości |
wartość składowej vn wektora prędkości |
wartość składowej ve wektora prędkości |
Wartość składowej vd wektora prędkości |
Model 1 |
|
|
X |
X |
X |
Model 2 |
|
|
|
|
|
Pomiar geodezyjny |
|
|
|
|
|
Komentarz:
Proszę napisać jak uzyskane wyniki z metody 1 mają się do tych z metody 2.
Jak ww. mają się z kolei do wyników pomiarów na stacji EPN (wieloletni trend podawany w serwisie http://www.epncb.oma.be/). W tym przypadku proszę porównać wyniki dla wszystkich trzech składowych wektora, wyznaczonych w metodzie 2 z tymi opublikowanymi w ww. serwisie. Ponadto proszę o interpretację wyników i podanie przyczyn ewentualnych rozbieżności pomiędzy modelowymi i pomierzonymi parametrami ruchu oraz odnieść uzyskane wyniki do tych wyznaczonych z pomiaru dla stacji KRAW http://www.epncb.oma.be/_networkdata/siteinfo4onestation.php?station=KRAW i wyniki po rozwinięciu:
…………….........................................................................................................................................
....................................................................................................................................................................
....................................................................................................................................................................
………........................................................................................................................................................
....................................................................................................................................................................
............................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
1
![]()
β - azymut wektora prędkości, β = 90-C
Dane do ćwiczenia:
Latitude of Euler pole: 50.6193232793378 [deg.]
Longitude of Euler pole: -112.274193489415 [deg.]
Angular velocity: 0.233720447153884 [deg./m.y.]
Rotation vector omega:-0.000981,-0.002395,0.003153
Wyszukiwarka