Miary efektywności zarządzania portfelem inwestycyjnym

Końcowym elementem procesu zarządzania portfelem inwestycyjnym jest ocena uzyskanych rezultatów, czyli ocena efektywności (rentowności) portfela.

Ogólnie biorąc ocena efektywności portfela polega na optymalizacji dwóch parametrów portfela za pomocą syntetycznej miary, uwzględniającej zarówno dochód, jak i ryzyko.

Dokonuje się tego poprzez porównanie stopy zwrotu z ocenianego portfela ze stopą zwrotu z innego portfela o równoważnym ryzyku, bądź też jej podzielenie przez pewną miarę ryzyka.

W zależności od sposobu uwzględnienia elementu ryzyka, tj. poprzez iloraz lub różnicę, miary efektywności dzielą się na wskaźnikowe i rezydualne (różnicowe).

Do pierwszej grupy należą przede wszystkim wskaźniki Sharpe'a i Treynora, natomiast do drugiej - wskaźnik Jensena.

Wskaźnik Sharpe'a

Ogólnie biorąc wskaźnik Sharpe'a jest to stosunek osiągniętych wyników inwestycyjnych do całkowitego poziomu ryzyka.

Miara ta jest określana często jako relacja dodatkowej stopy zwrotu do zmienności, lub inaczej, jest równa premii za ryzyko przypadającej na jednostkę podjętego ryzyka.

Wartość wskaźnika Sharpe'a jest obliczana w następujący sposób:

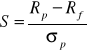
gdzie:

S - wskaźnik Sharpe'a.

R_p - przeciętna stopa zwrotu badanego portfela w analizowanym okresie,

R_f - przeciętna stopa zwrotu z instrumentu wolnego od ryzyka w analizowanym okresie,

σ_p - odchylenie standardowe badanego portfela w analizowanym okresie.

Wskaźnik Sharpe'a wyrażony jest wielkością niemianowaną. Jego interpretacja jest następująca: lepsze są te inwestycje, dla których wskaźnik jest większy.

Wskaźnik Sharpe'a można przedstawić graficznie (wykres 1).

Wykres 1. Wskaźnik Sharpe'a w ujęciu graficznym

Najlepszy portfel (A) usytuowany jest na najwyżej położonej półprostej, która wychodzi z punktu R_f. Jest to równoznaczne ze stwierdzeniem, że jest to półprosta o największym nachyleniu. Nachylenie to jest wyrażone właśnie wskaźnikiem Sharpe'a.

Ogólnie biorąc, za pomocą wskaźnika Sharpe'a możemy uszeregować portfele inwestycyjne od najbardziej do najmniej efektywnych, przy czym najbardziej efektywnym jest portfel, który leży na linii o największym nachyleniu w układzie ryzyko całkowite - zwrot dodatkowy.

Wskaźnik Sharpe'a może mieć wartości ujemne. Występuje to w sytuacji, gdy w danym okresie stopa zwrotu portfela jest niższa niż stopa zwrotu z instrumentu wolnego od ryzyka.

Wskaźnik Treynora

Drugą, obok wskaźnika Sharpe'a, miarą efektywności portfela jest podobny wskaźnik opracowany przez J. Treynora, różniący się jedynie sposobem zdefiniowania ryzyka.

Wskaźnik Treynora można obliczyć za pomocą następującego wzoru:

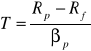
gdzie:

T - wskaźnik Treynora,

β_p - współczynnik beta badanego portfela w analizowanym okresie,

pozostałe oznaczenia jak w poprzednim wzorze.

Wskaźnik Treynora wyrażany jest w procentach. Im większa wartość wskaźnika, tym lepszy portfel dla wszystkich inwestorów (pomijając ich stosunek do ryzyka).

W ujęciu graficznym wskaźnik Treynora można przedstawić jako współczynnik kierunkowy prostej łączącej punkt reprezentujący w przestrzeni (R, β) wybrany portfel z punktem o odciętej zero i rzędnej równej stopie zwrotu wolnej od ryzyka (R_f) - wykres 2.

Wykres 2. Wskaźnik Treynora w ujęciu graficznym

Podobnie jak w przypadku wskaźnika Sharpe'a, portfel o większym nachyleniu jest korzystniejszy dla inwestora niezależnie od jego skłonności do ryzyka, ponieważ większa wartość wskaźnika umożliwia zawsze uzyskanie wyższej użyteczności.

Rankingi według wskaźnika Treynora są podobne do rankingów według wskaźnika Sharpe'a, ponieważ miary te różnią się jedynie sposobem definiowania ryzyka.

Wskaźnika Treynora, podobnie jak i Sharpe'a, nie można używać do porównywania stóp zwrotu uzyskanych w różnych okresach. Miara ta jest bowiem wrażliwa na ogólne tendencje całego rynku akcji.

Wskaźnik Jensena

Wskaźnik Jensena jest ulepszeniem wskaźnika Treynora uwzględniającym w ocenie koniunkturę panującą na giełdzie. Wartość tworzoną przez zarządzającego portfelem mierzą tu odchylenia danego portfela od stanu równowagi postulowanego przez model rynku kapitałowego (CAPM).

W przypadku wskaźnika Jensena i innych miar różnicowych, ryzyko korygowane jest poprzez odjęcie dochodów, jakich przy tym ryzyku należało oczekiwać na mocy pewnego modelu od dochodów faktycznie osiągniętych przez zarządzającego portfelem.

W uproszczeniu można powiedzieć, że obliczając wskaźnik Jensena od stopy zwrotu z danego portfela odejmuje się stopę zwrotu z indeksu rynku akcji, jednak tylko w tej części, w jakiej zarządzający portfelem faktycznie inwestuje w akcje.

Wskaźnik Jensena liczymy za pomocą następujących wzorów:

gdzie:

J - wskaźnik Jensena,

R_w - stopa zwrotu z portfela wzorcowego,

R_m - rynkowa stopa zwrotu (np. z indeksu giełdy),

β_p - współczynnik beta portfela,

pozostałe oznaczenia jak w poprzednich wzorach.

Wzór na stopę zwrotu portfela wzorcowego jest taki sam jak równanie linii rynku papierów wartościowych (SML) w modelu CAPM.

Interpretacja graficzna wskaźnika Jensena przedstawiona jest na wykresie 3.

Wykres 3. Wskaźnik Jensena w ujęciu graficznym

Dodatni wskaźnik Jensena, czyli stopa zwrotu z portfela przekraczająca stopę oczekiwaną jest oznaką posiadania przez zarządzającego portfelem informacji poufnej lub umiejętności wyboru ze zbioru możliwości inwestycyjnych aktywów niedowartościowanych.

Natomiast wskaźnik ujemny oznacza ponoszenie nadmiernych kosztów na analizę papierów wartościowych, zbyt wysokich w stosunku do płynących z tej analizy korzyści.

Zerowy wskaźnik Jensena jest postulowany przez hipotezę rynków efektywnych, tzn. brak możliwości osiągania ponadprzeciętnych dochodów, czyli „pokonania rynku”, bierze się w myśl tej hipotezy z braku występowania na rynkach finansowych informacji mających jeszcze jakiś wpływ na ceny akcji.

D

C

B

A

R_f

R

σ

A, B, C, D - portfele

D

C

B

A

R_f

R

β

A, B, C, D - portfele

R

β

R_p

R_m

R_w

R_f

β_m

β_p

M

J

SML

---