Podstawy automatyki

Dla:

• T₁=1;

• T₂=2;

• T₃=1;

Szukane:

h(t), g(t), P(ω), Q(ω), A(ω), φ(ω), L(ω);

Obliczenia:

Liczymy transmitancje

G(s)=
;

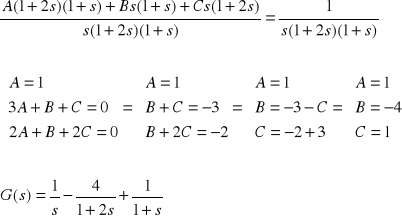
Liczymy transmitancje charakterystyczną:

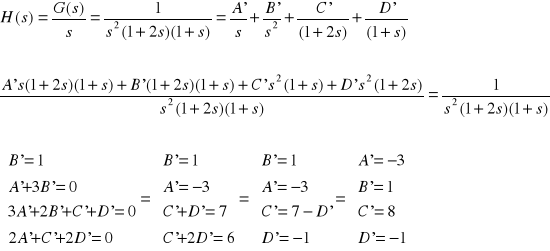
Odwrotną transmitancje G(s) i H(s):

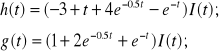
Liczymy transmitancje widmową (s=jω):

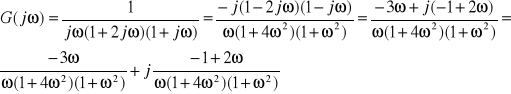
G(jω)=P(ω)+jQ(ω);

P(ω)=
;

Q(ω)=
;

Z wzoru Eulera:

P²(ω)+jQ²(ω)=A(ω)e^jφ(ω)

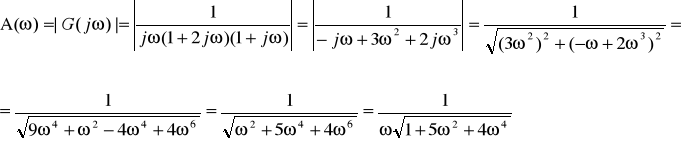
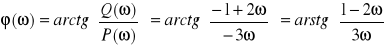
Obliczamy postać logarytmiczną:

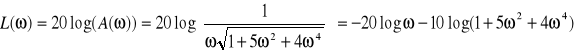
Wykresy:

Dla

Dla

Dla P(ω)=
;

Dla Q(ω)=

Dla

Dla

Dla

Ω
∞

g(t)
0

Ω
∞

h(t)
∞

ω

ω

ω

ω

ω

ω

ω

Ω
∞

P(ω)
0

Ω
∞

Q(ω)
0

ω

ω

ω

ω

ω

ω

Ω
0

A(ω)
∞

Ω
∞

A(ω)
0

Ω
0

Q(ω)
-∞

Ω
0

P(ω)
-3

Ω
0

g(t)
4

Ω
0

h(t)
0

Ω
0

φ(ω)
π/2

Ω
∞

φ(ω)
-π/2

ω

ω

φ

ω

ω

ω

ω

Ω
∞

L(ω)
-∞

Ω
0

L(ω)
∞