Politechnika Krakowska Fizyka Techniczna II Rok |
Marcin Bernady |
Rok akad.: 1999/2000 |
Data: 23.11.1999 |
||
Grupa 2 Zespół 3 |
|
Nr ćwicz.: 40 |
Ocena:
|
Podpis:
|
|
Dyfrakcja i Interferencja Światła Lasera na Szczelinach
Źródłami światła mogą być ciała, których atomy zostały wzbudzone na wyższy poziom energetyczny o energii E2 i powracając do stanu o niższej energii E1 emitują kwanty promieniowania elektromagnetycznego o energii hν odpowiadającej różnicy:
![]()
gdzie h jest stałą Plancka, ν - częstotliwością promieniowania. Podczas emisji spontanicznej, która zachodzi bez czynnika z zewnątrz, atomy źródła wysyłają promieniowanie niezależnie od siebie, w przypadkowych kierunkach, z różnymi fazami i o różnych płaszczyznach polaryzacji. Światło to jest więc światłem niespójnym.
Atomy znajdujące się w niższym energetycznie stanie E1 mogą zostać pobudzone do przejścia do stanu wyższego energetycznie E2 w procesie absorpcji promieniowania elektromagnetycznego o energii hν odpowiadającej różnicy poziomów obu stanów. Możliwy jest jeszcze trzeci rodzaj przejść zwany emisją wymuszoną. W procesie tym padający foton pobudza atom do przejścia z wyższego do niższego stanu energetycznego. Liczba fotonów wzrasta, gdyż oprócz fotonu padającego (wymuszającego) pojawia się jeszcze foton wyemitowany przez atom (wymuszony), posiadający tę samą energię i fazę oraz rozprzestrzeniający się w tym samym kierunku. Wiązka promieniowania powstała w wyniku emisji wymuszonej będzie posiadać duże natężenie, będzie stosunkowo mało rozbieżna, monochromatyczna i spójna. Zjawisko to znalazło zastosowanie w urządzeniach zwanych laserami.
W warunkach równowagi termodynamicznej liczba atomów znajdujących się w stanie podstawowym znacznie przewyższa liczbę atomów w stanach wzbudzonych. W takich warunkach absorpcja światła padającego będzie znacząco większa od emisji wymuszonej. W celu osiągnięcia przewagi drugiego rodzaju przejść, trzeba doprowadzić do zwiększenia ilości atomów wzbudzonych, czyli do inwersji obsadzeń. Wówczas przy odpowiednich warunkach pojedynczy foton może wymusić lawinową emisję fotonów identycznych z wymuszającym.
W laserach inwersję obsadzeń poziomów energetycznych uzyskuje się w procesie tzw. pompowania. Bombardując atomy w stanie E0 strumieniem elektronów o odpowiednio dużej energii kinetycznej lub pobudzając je promieniowaniem, wzbudzamy je do poziomu E2. Jest on poziomem krótkożyjącym i atomy przechodzą z niego do stanu podstawowego lub na długożyjący (metatrwały) poziom E1. Poziom metatrwały zapełnia się i zostaje osiągnięta inwersja obsadzeń.
Do uzyskania inwersji obsadzeń konieczne jest istnienie trzech poziomów energetycznych, z których jeden jest długożyjącym.
Każdy laser składa się z trzech zasadniczych elementów: materiału aktywnego, układu pompującego i układu zwierciadeł (rezonatora). Rezonator, to układ dwóch zwierciadeł, pomiędzy którymi umieszcza się materiał aktywny. Poprzez wielokrotne odbicia od zwierciadeł, rezonator ma na celu zapobiec opuszczeniu układu przez fotony i zapewnić lawinowy rozwój emisji wymuszonej. Jedno ze zwierciadeł jest częściowo przepuszczalne, aby wiązka mogła wydostać się na zewnątrz. Fotony rozchodzące się w innych kierunkach niż prostopadły do zwierciadeł, opuszczają układ i wiązka wychodząca na zewnątrz jest prawie równoległa (skolimowana).
Z falową naturą światła związane są zjawiska interferencji i dyfrakcji.
Zjawisko polegające na uginaniu się promieni świetlnych padających na przeszkody lub przechodzących przez szczeliny nazywamy dyfrakcją. Efekty dyfrakcyjne są silne wówczas, gdy rozmiary obiektów znajdujących się na drodze fali świetlnej są porównywalne z jej długością λ. Jeśli za wąską szczelinę o szerokości a, na którą pada fala świetlna o długości λ umieścimy ekran w odległości L>>a, to będziemy na nim obserwować układ jasnych i ciemnych prążków o zmieniającym się natężeniu. Powstanie takiego obrazu dyfrakcyjnego możemy wytłumaczyć na podstawie zasady Huyghensa i zjawiska interferencji. Położenia ciemnych prążków są dane warunkiem:
![]()
gdzie n jest liczbą całkowitą, a - szerokością szczeliny.
Z zależności tej widać, że obraz dyfrakcyjny światła na jednej szczelinie zależy od stosunku λ/a. Zmieniając szerokość szczeliny możemy zmieniać położenie pierwszego ciemnego prążka.
Zjawisko dyfrakcji można łatwo zaobserwować w przypadku światła lasera. Jest ono bowiem w wysokim stopniu monochromatyczne i skolimowane, w przeciwieństwie do źródeł konwencjonalnych i nie zachodzi zacieranie się obrazu dyfrakcyjnego poprzez nakładanie się na siebie obrazów dyfrakcyjnych różnych długości fal czy też wytworzonych przez odległe punkty powierzchni światła.
Interferencja fal polega na nakładaniu się dwu lub więcej fal harmonicznych o tej samej długości, prowadzącym do powstania ustalonego w czasie przestrzennego rozkładu obszarów wzmocnienia i osłabienia fali wypadkowej. Zjawisko to możemy zaobserwować, gdy światło pada na dwie szczeliny. Jeśli długość fali świetlnej λ jest większa od szerokości każdej ze szczelin, to przechodzące przez nie i ugięte fale dają obraz interferencyjny składający się na przemian z jasnych i ciemnych prążków o prawie jednakowym natężeniu. W określonym punkcie P ekranu obserwujemy prążek jasny, jeśli dociera do niego równocześnie maksimum pierwszej i drugiej fali. Wówczas bowiem zachodzi sumowanie się amplitud fal wypadkowych. W przypadku, gdy w rozważanym punkcie P spotyka się minimum jednej i maksimum drugiej fali, dochodzi do wygaszenia fal.
Zjawiska interferencji i dyfrakcji rzadko występują oddzielnie. Dla realnych szczelin, których są większe lub porównywalne z długością fali świetlnej natężenie uzyskanego obrazu interferencyjnego będzie modulowane przez czynnik dyfrakcyjny. Uzyskane prążki interferencyjne będą miały wyraźnie zmieniające się natężenie, zależne od obrazu dyfrakcyjnego od pojedynczej szczeliny.
Dyfrakcja światła lasera na jednej szczelinie
Wyniki pomiarów zamieszczam poniżej w tabeli.
y [mm] |
U [V] |
-23 |
0,06 |
-22 |
0,07 |
-21 |
0,07 |
-20 |
0,07 |
-19 |
0,08 |
-18 |
0,09 |
-17 |
0,09 |
-16 |
0,09 |
-15 |
0,11 |
-14 |
0,14 |
-13 |
0,13 |
-12 |
0,13 |
-11 |
0,19 |
-10 |
0,25 |
-9 |
0,25 |
-8 |
0,27 |
-7 |
0,46 |
-6 |
0,77 |
-5 |
0,79 |
-4 |
1,00 |
-3 |
3,00 |
-2 |
9,50 |
-1 |
16,7 |
0 |
23,0 |
1 |
22,7 |
2 |
16,4 |
3 |
7,90 |
4 |
3,30 |
5 |
1,00 |
6 |
0,90 |
7 |
0,70 |
8 |
0,30 |
9 |
0,20 |
10 |
0,28 |
11 |
0,16 |
12 |
0,12 |
13 |
0,15 |
14 |
0,14 |
15 |
0,09 |
16 |
0,08 |
17 |
0,09 |
18 |
0,09 |
19 |
0,07 |
20 |
0,05 |
21 |
0,07 |
Na podstawie tych danych został narysowany wykres zależności natężenia światła, które jest proporcjonalne do mierzonego napięcia, od odległości od głównego max
![]()
Korzystając z wykresu odczytujemy położenia kolejnych minimów:
n = 1 y1 = 5 mm
n = 2 y2 = 9 mm
n = 3 y3 = 12 mm
n = 4 y4 = 16 mm
n = 5 y5 = 20 mm
Dla, których to obliczamy szerokość szczeliny a, zgodnie z wzorem
![]()
oraz błędy pomiarowe
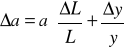
gdzie:
L = (1,070 ± 0,005) m - odległość układu pomiarowego od źródła światła
λ = 670 nm - długość fali światła lasera
Δy = ± 1 mm
Zatem szerokość szczeliny, dla poszczególnych minimów wynosi
a1 = (143 ± 29) μm błąd procentowy - 20%
a2 = (159 ± 18) μm błąd procentowy - 11%
a3 = (179 ± 15) μm błąd procentowy - 8,4%
a4 = (179 ± 15) μm błąd procentowy - 8,4%
a5 = (179 ± 15) μm błąd procentowy - 8,4%
Wartość średnia szerokości szczeliny : aśr = (167,8 ± 16,3) μm.
Dyfrakcja światła lasera na siatce dyfrakcyjnej
Wyniki pomiarów zamieszczam poniżej.
y [mm] |
U [V] |
0 |
6,30 |
10 |
6,60 |
20,5 |
0,69 |
-10 |
8,20 |
-20,5 |
0,50 |
Mając położenie prążków dyfrakcyjnych pierwszego i drugiego rzędu można obliczyć stałą siatki dyfrakcyjnej, zgodnie ze wzorem
![]()
oraz błędy pomiarowe
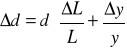
n = 1 d1 = (6,96 ± 0,73) μm
n = 2 d2 = (11,0 ± 0,6) μm
Zatem stała siatki wynosi : dśr = (8,98 ± 2,86) μm.
Dyfrakcja światła lasera na układzie dwóch siatek dyfrakcyjnych
W doświadczeniu użyliśmy dwóch siatek dyfrakcyjnych, nawzajem do siebie prostopadłych. Stanowią one model dwuwymiarowej sieci krystalicznej. Światło ulega na tym układzie dyfrakcji, podobnie jak promieniowanie rentgenowskie na atomach kryształu.
Wnioski
1. Szerokość szczeliny wyniosła 167,8 μm, zatem spełnione są nierówności:
![]()
![]()
oraz
![]()
![]()
2. Również stała siatki spełnia nierówność
![]()
![]()
3. Błędy wynikają z niedokładności pomiarowych związanych z przyrządami pomiarowymi, ale również związane są z parametrami wiązki lasera, które nie były idealne.
1
5
Wyszukiwarka