Nr ćwiczenia: 14	Imię i nazwisko:	Nr zespołu: VIII	Data 11.03.98r.
Wydział Inżynierii Elektrycznej Gr. 12	Temat ćwiczenia: Wyznaczanie współczynnika lepkości dynamicznej cieczy.	Ocena	Podpis

Tarcie wewnętrzne (lepkość) jest zjawiskiem międzycząsteczkowym i polega na oddziaływaniu sąsiednich warstw cieczy na siebie w czasie przepływu.

Wyobraźmy sobie dwie sąsiadujące ze sobą warstwy cieczy odległe od siebie o małą skończoną odległość Δx i płynącą z bardzo małą różnicą prędkości ΔV.

A V+ΔV B

Δx

C V D

Warstwa AB o większej prędkości przyspiesza ruch warstwy wolniejszej CD i dzięki temu sama doznaje hamowania, siła tarcia działająca pomiędzy tymi warstwami wyraża się wzorem:

s -powierzchnia warstw

η -współczynnik lepkości cieczy

Współczynnik lepkości cieczy η jest to stosunek ciśnienia stycznego p wywołującego przesuwanie się jednych warstw cieczy po drugich do gradientu /spadku/ prędkości V w cieczy
.

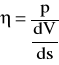
s - odstęp warstw liczony prostopadle do wektora prędkości .

η jest dla danej cieczy (należącej do grupy cieczy, zwanych newtonowskimi) wielkością stałą, zależną w wysokim stopniu od temperatury.

η- współczynnik lepkości

K- stała Boltzmana

T- temperatura bezwzględna

B- tzw. Energia aktywacji

Jednostką współczynników lepkości jest 1 N*m/m².

Gęstością lub masą właściwą (dla ciał jednorodnych) nazywamy stosunek masy do objętości.

Wyznaczanie współczynnika lepkości dynamicznej cieczy na podstawie prawa Stokesa.

Prawo Stokesa podaje wielkość oporu W, jakiego doznaje mała kulka poruszająca się w bardzo lepkiej cieczy (tak lepkiej, że opory bezwładne są małe w porównaniu z oporami tarcia), jako funkcję prędkości kulki V, jej promienia r i współczynnika lepkości cieczy η:

W=6*Π*η*r*V.

W przypadku kulki spadającej pionowo ruchem jednostajnym w ośrodku lepkim opór ten jest zrównoważony wypadkową ciężaru kulki G

G=
ρ₁g

I parcia hydrostatycznego P

P=
πr³ρ₂g

gdzie:

ρ₁ ,ρ₂ -odpowiednio gęstość kulki i gęstość cieczy,

g - przyspieszenie ziemskie

Warunek równowagi sił ma postać:

6πηVr =
πr³g(ρ₁-ρ₂)

skąd:

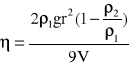
W celu wyznaczenia η musimy zmierzyć promień kulki r, gęstość kulki i cieczy ρ₁ i ρ₂ oraz prędkość ruchu V.

Tabl. Wyznaczanie gęstości oleju.

h1 [cm]	h2 [cm]	h3 [cm]	h1-h3 [cm]	h2-h3 [cm]	ρw [kg/m^3]	τ [^oC]	ρo [kg/m^3]
36,1	-40,5	12,5	23,6	28	997,296	24	840,578

Kulka 1	2r [mm]	T [s]	S1 [cm]	S2 [cm]	S1-S2 [cm]	η [Ns/m^2]	ηo [Ns/m^2]	2R [cm]
1	2,55	59,90	33,9	11,3	22,6	0,150	0,139	7,4
2	2,55	60,10				0,150	0,139
3	2,54	57,10				0,142	0,131
4	2,54	57,40				0,142	0,131
5	2,56	59,20				0,149	0,138
6	2,55	59,00				0,147	0,136
7	2,54	58,20				0,144	0,133
8	2,56	58,40				0,147	0,136
9	2,55	59,10				0,148	0,137
10	2,55	58,50				0,146	0,135
Kulka 2
1	2,35	61,60				0,131	0,122
2	2,36	61,80				0,132	0,123
3	2,35	60,10				0,128	0,119
4	2,35	60,00				0,127	0,118
5	2,36	58,40				0,125	0,116
6	2,34	59,50				0,125	0,116
7	2,35	60,00				0,127	0,118
8	2,35	60,10				0,128	0,119
9	2,35	59,50				0,126	0,117
10	2,36	59,60				0,127	0,118
Kulka 3
1	2,30	60,10				0,122	0,114
2	2,31	60,00				0,123	0,114
3	2,30	60,10				0,122	0,114
4	2,30	61,00				0,124	0,115
5	2,30	60,50				0,123	0,114
6	2,31	60,00				0,123	0,114
7	2,30	60,10				0,122	0,114
8	2,30	60,20				0,122	0,114
9	2,29	60,50				0,122	0,114
10	2,30	60,50				0,123	0,114

Wniosek:

Liczba Reynoldsa dla każdej z kulek wyszła nam mniejsza od 0,4 zatem możemy dla nich uznać prawo Stokesa za wiarygodne. Siły lepkości odgrywają znaczącą rolę w ruchu cieczy, gdyż liczby Reynoldsa wyszły nam bardzo małe.

Wyznaczanie współczynnika lepkości dynamicznej cieczy

---