Politechnika Śląska w Gliwicach
Laboratorium Podstaw Miernictwa
Błędy Systematyczne i Przypadkowe
Grupa : 1
Sekcja : 6
Danuta Kapica
Jerzy Mańka
Piotr Bugiel
Gliwice 1996 -12-10
Wprowadzenie
Celem ćwiczenia jest poznanie charakteru błędów systematycznych i przypadkowych, sposobów ich doświadczalnego wyznaczania oraz metod stosowanych w procesie opracowywania wyników pomiaru.
Przebieg ćwiczenia
2.1 Charakterystyka błędów systematycznych i przypadkowych
Błąd systematyczny jest to błąd, który przy wielokrotnym wykonywaniu pomiaru tej samej wartości wielkości mierzonej w tych samych warunkach ma wartość stałą lub zmienia się według określonego prawa. Błędy przypadkowe mają wartość zmieniającą się losowo, dla każdego pomiaru tej samej wielkości mają nieznaną przypadkową wartość.
2.2 Przetwornik indukcyjnościowy
Przetwornik indukcyjnościowy służy do przetwarzania przesunięć mechanicznych na wielkości elektryczne. Zmieniając położenie rdzenia, zmieniamy impedancje Z1 i Z2, przez co zmienia się równowaga mostka. Jest to przyczyną zmian napięcia Uwy. W ćwiczeniu wykonaliśmy trzy serie pomiarów napięcia niezrównoważenia mostka będących miarą przesunięcia rdzenia. W każdej serii odczytywaliśmy napięcie dla przesunięć co jeden centymetr. Schemat układu pomiarowego przedstawia rysunek 1, a otrzymane wyniki przedstawia rysunek 2, oraz poniższa tabela.
Przesunięcie [cm] |
Napięcie 1 seria [V] |
Napięcie 2 seria [V] |
Napięcie 3 seria [V] |
Napięcie średnie [V] |
1 |
1.7 |
1.7 |
1.7 |
1.7 |
2 |
1.8 |
1.8 |
1.8 |
1.8 |
3 |
1.8 |
1.8 |
1.8 |
1.8 |
4 |
1.6 |
1.6 |
1.6 |
1.6 |
5 |
1 |
1.1 |
1.1 |
1.066667 |
6 |
0.3 |
0.3 |
0.3 |
0.3 |
7 |
-0.6 |
-0.6 |
-0.6 |
-0.6 |
8 |
-1.3 |
-1.3 |
-1.3 |
-1.3 |
9 |
-1.8 |
-1.8 |
-1.8 |
-1.8 |
10 |
-2 |
-2 |
-2 |
-2 |
11 |
-1.9 |
-1.9 |
-1.9 |
-1.9 |
12 |
-1.6 |
-1.6 |
-1.6 |
-1.6 |
13 |
-1 |
-1.1 |
-1.1 |
-1.066667 |
14 |
-0.6 |
-0.5 |
-0.5 |
-0.5333334 |
15 |
-0.2 |
-0.2 |
-0.2 |
-0.2 |
Rysunek 1 : Schemat układu pomiarowego.
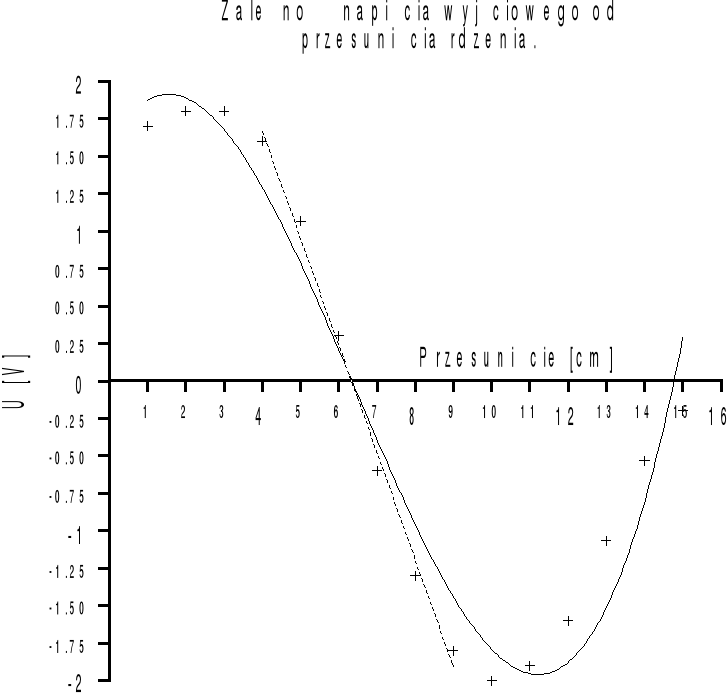
Rysunek 2 : Zależność napięcia nierównowagi mostka od przesunięcia rdzenia.
Na wykresie Zostały zaznaczone punkty odpowiadające wartościom średnim napięcia z trzech serii. Krzywa aproksymująca otrzymane wyniki jest opisana równaniem trzeciego stopnia w postaci:
Dodatkowo w liniowej części aproksymowaliśmy charakterystykę linią prostą o równaniu:
Największą odchyłkę od krzywej aproksymującej otrzymaliśmy dla przesunięcia 9 [cm] i wyniosła 0.45 [V].
L.P. |
U [V] |
1 |
0.93 |
2 |
0.95 |
3 |
0.90 |
4 |
0.89 |
5 |
0.87 |
6 |
0.89 |
7 |
0.89 |
8 |
0.90 |
9 |
0.92 |
10 |
0.94 |
11 |
0.90 |
12 |
0.93 |
13 |
0.90 |
14 |
0.89 |
15 |
0.93 |
Następnie wykonaliśmy 15 - krotny pomiar Uwy dla jednej wartości przesunięcia (5 [cm]). Wyniki otrzymane przedstawia tabela obok. Z otrzymanego zbioru wartości obliczyliśmy :
Następnie dla parametrów N = 15, t = 1.96, α = 0.95 obliczyliśmy :
Korzystając z zależności :
<a -3σ ; a +3σ> ≈ <xśr - 3Sx ; xśr + 3Sx>
wykonaliśmy test na to, czy nasze pomiary nie są obarczone błędem grubym. Na podstawie uzyskanego w ten sposób przedziału ufności - <0,8413 ; 0,9787 > - stwierdziliśmy, że wszystkie pomiary nie są obarczone błędem grubym (wszystkie wartości otrzymane z pomiarów mieszczą się o obliczonym przedziale ufności.
2.3 Przetwornik elektrokonduktometryczny
Rysunek 3 : Schemat układu pomiarowego.
Przetwornik ten stosowany jest do pomiarów stężenia elektrolitów. W ćwiczeniu tym wykonaliśmy pomiary prądu i napięcia płynącego pomiędzy elektrodami zanurzonymi w wodzie dla różnych temperatur. Schemat układu pomiarowego wykorzystanego w tej części ćwiczenia przedstawia rysunek 3.
W tej części ćwiczenia otrzymane wyniki zostały przybliżone prostą. Ze względu na niewielką ilość pomiarów narysowaliśmy charakterystykę tylko dla przedziału temperatur, dla którego dokonaliśmy pomiarów.
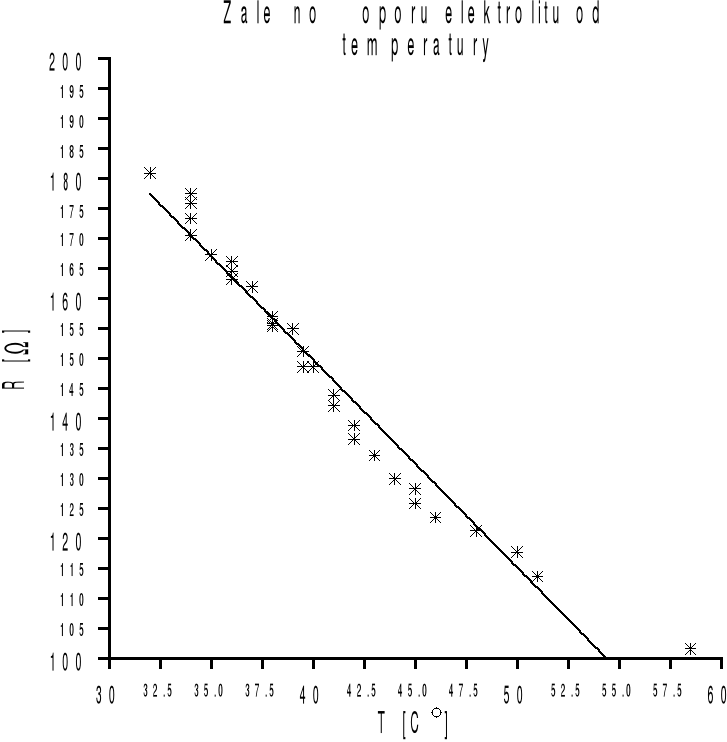
Rysunek 4 : Zależność rezystancji elektrolitu od temperatury.
Błędy popełnione przy obliczaniu oporu elektrolitu przedstawia poniższa tabela. Błąd został obliczony za pomocą metody różniczki zupełnej.
L.P. |
Napięcie [V] |
Prąd [A] |
Opór [W] |
Błąd [W] |
1 |
9.9 |
0.0975 |
101.5385 |
4.6391 |
2 |
10 |
0.0880 |
113.6364 |
5.3461 |
3 |
10 |
0.0850 |
117.6471 |
5.6055 |
4 |
10 |
0.0825 |
121.2121 |
5.8402 |
5 |
10 |
0.0810 |
123.4568 |
5.9899 |
6 |
10 |
0.0795 |
125.7862 |
6.1469 |
7 |
10 |
0.0780 |
128.2051 |
6.3116 |
8 |
10 |
0.0770 |
129.8701 |
6.4260 |
9 |
10.1 |
0.0755 |
133.7748 |
6.6313 |
10 |
10.1 |
0.0740 |
136.4865 |
6.8207 |
11 |
10.2 |
0.0735 |
138.7755 |
6.9138 |
12 |
10.3 |
0.0725 |
142.0690 |
7.0773 |
13 |
10.5 |
0.0730 |
143.8356 |
7.0651 |
14 |
10.4 |
0.0700 |
148.5714 |
7.4694 |
15 |
10.4 |
0.0700 |
148.5714 |
7.4694 |
16 |
10.1 |
0.0680 |
148.5294 |
7.6882 |
17 |
10.2 |
0.0675 |
151.1111 |
7.8025 |
18 |
10.3 |
0.0665 |
154.8872 |
8.0050 |
19 |
10.2 |
0.0655 |
155.7252 |
8.1464 |
20 |
10.1 |
0.0650 |
155.3846 |
8.2012 |
21 |
10.2 |
0.0650 |
156.9231 |
8.2367 |
22 |
10.2 |
0.0650 |
156.9231 |
8.2367 |
23 |
10.2 |
0.0630 |
161.9048 |
8.6168 |
24 |
10.3 |
0.0620 |
166.1290 |
8.8580 |
25 |
10.2 |
0.0625 |
163.2000 |
8.7168 |
26 |
10.2 |
0.0620 |
164.5161 |
8.8189 |
27 |
10.2 |
0.0610 |
167.2131 |
9.0298 |
28 |
10.4 |
0.0610 |
170.4918 |
9.1105 |
29 |
10.4 |
0.0600 |
173.3333 |
9.3333 |
30 |
10.2 |
0.0580 |
175.8621 |
9.7206 |
31 |
10.2 |
0.0575 |
177.3913 |
9.8450 |
32 |
10.2 |
0.0575 |
177.3913 |
9.8450 |
33 |
10.4 |
0.0575 |
180.8696 |
9.9357 |
Następnie przeprowadziliśmy test polegający na sprawdzeniu czy w czasie, który upłynął pomiędzy pierwszymi pięcioma pomiarami, a ostatnimi pięcioma pomiarami wartość wielkości mierzonej uległa zmianie . W tym celu obliczyliśmy średnie z pięciu pierwszych i pięciu ostatnich pomiarów (xśr1, xśr2). Dla N1 = N2 = 5 otrzymaliśmy :
Oszacowaliśmy także łącznie wariancje z obu próbek :
Dla założonych parametrów (α, t, N1, N2) badamy czy spełniona jest następująca nierówność :
Jeśli jest ona spełniona, to wartość wielkości mierzonej nie uległa zmianie. W przeciwnym razie możemy stwierdzić z prawdopodobieństwem (1- α), że wielkość wartości mierzonej uległa zmianie. W naszym przypadku dla N1 = N2 = 5, α = 0.95, t = 1.96, po podstawieniu otrzymujemy :
-7,97 ≤ xśr1 - xśr2 ≤+7,97
-7,97 ≤ -61,47 ≤+7,97
Więc w naszym przypadku, wartość wielkości mierzonej zmieniła się w trakcie wszystkich pomiarów.
Wnioski
Przetwornik indukcyjnościowy
Pomiary napięcia nierównowagi mostka są obarczone błędami przypadkowymi wynikającymi z niedokładności ustawienia rdzenia oraz odczytu wskazań miernika. Wykonaliśmy kilka serii pomiarów dla tych samych przesunięć aby zmniejszyć wpływ powyższych błędów na wynik pomiaru. Aproksymując otrzymaną charakterystykę krzywą trzeciego stopnia popełniamy największy błąd rzędu kilkunastu procent. Dla części charakterystyki odpowiadającej przesunięciom od 4 do 9 [cm] aproksymując otrzymane punkty prostą uzyskujemy błąd pomijalnie mały.
3.2 Przetwornik elektrokonduktometryczny
Błędy w tej części ćwiczenia wynikają z metody wybranej do pomiaru napięcia i prądu. Zastosowaliśmy tutaj metodę poprawnie mierzonego prądu, co spowodowało, że pomiar napięcia był obarczony błędem systematycznym. Również aproksymacja prostą otrzymanej charakterystyki rzeczywistej wnosi dodatkowe błędy nie przekraczające jednak kilku procent. Ponieważ nie dysponowaliśmy odpowiednimi danymi nie mogliśmy obliczyć współczynnika korekcyjnego. Oszacowaliśmy tylko błąd odczytu wynikający z niedokładności miernika.
Laboratorium Podstaw Miernictwa : „Błędy systematyczne i przypadkowe”
Grupa : 1, Sekcja : 6
7
7
Wyszukiwarka