Politechnika Warszawska Wydział Elektryczny Zakład Elektrotechniki Teoretycznej		Laboratorium Elektrotechniki Teoretycznej
Rok Semestr Gr.	Data godz.	Ćwiczenie nr 1 Temat: Badani obwodów jednofazowych RLC przy wymuszeni sinusoidalnym.
Zespół nr :		Prowadzący:	Ocena: 4 pkt/4

1. Cel ćwiczenia:

Celem ćwiczenia jest zapoznanie z rozkładem napięć, prądów i mocy w obwodach złożonych z rezystorów, cewek i kondensatorów w różnych układach połączeń, a następnie wykonanie koniecznych obliczeń na liczbach zespolonych oraz narysowanie wykresów wektorowych, a także obserwacja i analiza

2. Wprowadzienie teoretyczne:

Dwójniki skonstruowane z elemetnów RLC podlegają prawom Kirchhoffa (prądowemu i napięciowemu).

Przy połączeniu szeregowym napięcia na poszczególnych elementach się dodają z uwzględnieniem odpowiednich zależności między prądem płynącym przez dany element a napięciem będącym na nim. Napiecie i prad na oporności są ze sobą w fazie. W przypadku cewki napiecie „wyprzedza” prąd o kąt 90 stopni zaś na kondenatorze „opóźnia” się o ten kąt.

Dla połączenia równoległegona wszystkich elementach jest to samo napięcie. Suma wektorowa prądów daje nam prąd całkowity. Można mówić o charakterze obwodu całokitego:

• Charakter indukcyjny jest wtedy gdy napięcie podawane na obwód wyprzedza prad całkowity.

• Charakter pojemnościowy jest wtedy gdy napięcie podawane na obwód opóźnia się względem prądu cąłkowitego.

• Charakter rezystancyjny gdy te napięcie jest w fazie z prądem wypadkowym.

Przy pomiarach kozysta się z tego że watomierz pokazuje wyłącznie moc czynną. Pozłużyć to może do obliczania rezystancji obwodu a docelowo do obliczania rezystancji uzwojenia cawki.

Całkowita moc wydzielana w układzie z elementami rezystancyjnymi, indukcyjnymi i pojemnościowymi nazywana jest mocą pozorną. Sama zaś moc na elementach indukcyjnych i pojemnościowych jest nazywana mocą bierną. Jedynie moc czynna jest zamieniana na ciepło.

3. Wykonanie ćwiczenia:

3.1 Badanie obwodów RLC bez sprzężeń magnetycznych

1. Obwód szeregowy RLC

W tym obwodzie będzie płynął jeden prąd I ,który wywoła spadki napięcia na poszczególnych elementach. Przy czym napięcie na opornikach zawsze jest w fazie z prądem płynącym przez te oporności. Natomiast napięcie na cewce wyprzeda prąd o 90º, a napięcie na kondensatorze musi się opóźniać w stosunku do prądu o kąt 90º (przypadek idealny).

2. Obwód równoległy GLC

W tym układzie napięcie będzie identyczne(wartość i kąt) na wszystkich elementach, natomiast prąd płynący przez cewkę będzie opóźniał się w stosunku do tego napięcia o kąt 90º (przypadek idealny) a odwrotnie będzie na kondensatorze tzn. prąd będzie wyprzedzał napięcie o kąt 90º.

3. Obwód szeregowo-równoległy RLC

W tym napięcia n oporniku i kondensatorze są w fazie i mają tą samą wartość. Jak wiemy prąd płynący przez rezystor jest zawsze w fazie z napięciem ,a prąd w kondensatorze wyprzedza napięcie o 90º. Po dodaniu wektorowo obu tych prądów uzyskamy prąd główny. Mając ten prąd możemy wyznaczyć napięcie na cewce wiedząc że będzie wyprzedzać prąd o 90º (przypadek idealny). Dodając wektorowo wszystkie napięcia wyznaczymy napięcie zasilające.

Dodatkowo należy zauważyć że rezystancje wewnętrzne cewek będą powodować że przesunięcia fazowe między prądem a napięciem nie będą wynosić dokładnie 90º czy -90º co zostało uwidocznione na wykresach.

Potrzebne wzory:

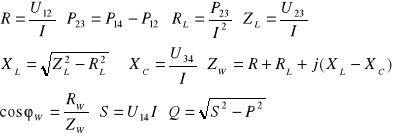
1.Przypadek a)

Pomiary
Uz	I	P14	P12	U12	U23	U34	U14
[V]	[A]	[W]	[W]	[V]	[V]	[V]	[V]
35	0,55	16,5	14,25	25,2	20,5	35	33,2

Tabela obliczeniowa:

Obliczenia
R	P23	RL	ZL	XL	ZL(zesp.)	XC	ZW(zesp.)	cosφw	φw	S	Q
[Ω]	[W]	[Ω]	[Ω]	[Ω]	[Ω]	[Ω]	[Ω]		o	[VA]	[var]
47,11	2,25	7,438	37,273	36,523	7,438+j36,523	63,64	54,848-j27,117	0,896	-26,31	18,26	7,82

2.Przypadek b)

Pomiary
Uz	I	P	I1	I2	I3	U14
[V]	[A]	[W]	[A]	[A]	[A]	[V]
23,3	0,62	12,5	0,45	0,54	0,32	20,7

Tabela obliczeniowa:

Obliczenia
R	PL	RL	XL	URL	UxL	XC	Z14(zesp.)	cosφw	φw	S	Q
[Ω]	[W]	[Ω]	[Ω]	[V]	[V]	[Ω]	[Ω]		o	[VA]	[var]
46	3,185	10,922	27,411	5,8981	14,80194	64,69	23,94+j11,19	0,906	25,05	12,83	2,9

3.Przypadek c)

Pomiary
Uz	I	P14	P12	I4	I5	U12	U24	U14
[V]	[A]	[W]	[W]	[A]	[A]	[V]	[V]	[V]
23,4	0,52	10,5	0,25	0,41	0,29	19	19	20,9

Tabela obliczeniowa:

Obliczenia
RL	ZL	XL	R	XC	PR	Z24(zesp.)	Z14(zesp.)	cosφw	φw	S	Q
[Ω]	[Ω]	[Ω]	[Ω]	[Ω]	[W]	[Ω]	[Ω]		o	[VA]	[var]
0,9246	36,538	36,53	46,341	65,517	10,25	30,9-j21,8	31,8+j14,73	0,907	24,85	10,87	2,8

2.2 Badanie obwodów ze sprzężeniami magnetycznymi:

Badania przeprowadziliśmy w układach pomiarowych przedstawionych poniżej, gdzie U_Z jest napięciem fazowym zasilacza trójfazowego. W przypadku d) sprzężenia ujemnego należało szeregowo ze źródłem napięcia włączyć rezystor R = 15Ω, w celu ograniczenia prądu płynącego przez małą rezystancję wypadkową.

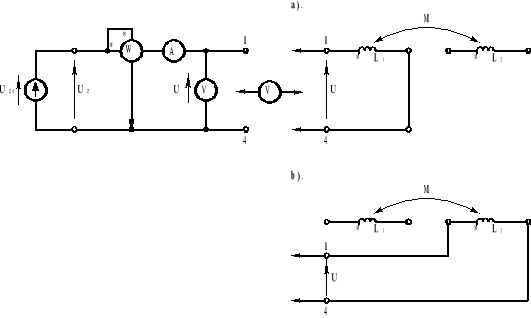
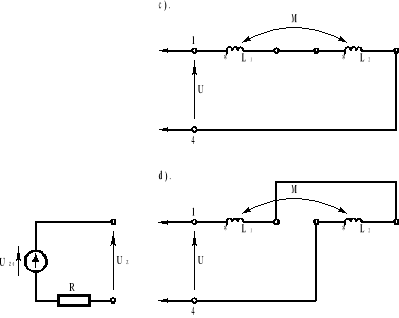
Otrzymane pomiary zamieszczone są w poniższej tabelce

	UZ	P	I	U	U1	U2
		V	W	A	V	V	V
a	11,7	1,5	0,49	10,3	10,3	8,5
b	11,67	2,25	0,56	9,95	9,89	9,95
c	47	5	0,68	43,5	23,8	21,4
d	23,1	4	0,92	5,6	3,86	2,5

Z otrzymanych pomiarów wyliczyliśmy następujące parametry cewek

	Z1	R1	XL1	L1	Z2	R2	XL2	L2	ZW	RW	LW	M	k
		Ω	Ω	Ω	H	Ω	Ω	Ω	H	Ω	Ω	H	H	-
a	21,02	6,25	20,07	0,064								0,055
b					17,77	7,17	16,26	0,052				0,056
c	35	6,25	20,07	0,064	31,47	7,17	16,26	0,052	63,97	10,81	0,2	0,043	0,75
d	4,2	6,25	20,07	0,064	2,72	7,17	16,26	0,052	6,09	4,73	0,12	0,052	0,9

Indukcyjność pierwszej cewki jest większa od indukcyjności drugiej, a rezystancja pierwszej jest mniejsza od drugiej. Sprzężenie magnetyczne dla cewek włączonych pojedynczo są ze sobą porównywalne, natomiast przy cewkach włączonych ze sprzężeniem magnetycznym sprzężenie to jest mniejsze dla sprzężenia dodatniego. Jest to efektem większej eksploatacji pierwszej cewki.

4. Wnioski:

(obliczenia teoretyczne dla Uzaś=Uzmierzone=20,7V)

	Szeregowy		Równoległy		Szeregowo-równoległy
Wyniki	zmierzona	obliczona	zmierzona	obliczona	zmierzona	obliczona
UR [V]	25,2	25,58	20,7=zaś	20,7	19	21,62
UL [V]	20,5	20,24	20,7	20,7	19	17,77
UC [V]	35	34,56	20,7	20,7	19	21,62
I [A]	0,55	0,543	0,62	0,65	0,52	0,587

Układ połączeń	Element
		R [Ω]	ZL [Ω]	XC [Ω]
Obwód szeregowy	47,11	7,438 + j36,523	63,64
Obwód równoległy	46	10,922 + j27,411	64,69
Obwód szeregowo-równoległy	46,341	0,9246 + j36,53	65,517
Średnia:	46,484	6,4482 + j33,488	64,616

W obwodzie szeregowym można było zauważyć, iż napięcia na elementach RLC dają napięcie zasilające, natomiast w obwodzie równoległym, że prądy płynące przez trzy gałęzie dają w sumie całkowity prąd I. Potwierdza to oba prawa Kirchhoffa (prądowe i napięciowe). Przy rozpatrywaniu obwodów trzeba było zwracać uwagę na zwroty napięć i prądów na elementach ponieważ napięcie na idealnej cewce wyprzedza prąd o a na kondensatorze napięcie opóźnia się w stosunku do prądu płynącego przez ten element o .

Jak już wcześniej zostało powiedziane cewka posiada również oprócz reaktancji - rezystancję która wynika z oporności drutu z którego jest wykonana. Ten parametr sprawia że cewce daleko jest do idealności i trzeba to uwzględnić w pomiarach, obliczeniach i wykresach.

Badaliśmy również obwody ze sprzężeniami magnetycznymi. W tej konfiguracji impedancja wypadkowa cewek wyraża się inaczej niż przy cewkach bez sprzężeń magnetycznych. Impedancja taka wynosi
i zależy od wzajemnego nawinięcia cewego względem siebie. Wartości R₁ oraz R₂ to rezystancje rzeczywistych cewek X_L1 i X_L2 to reaktancje tych cewek a X_M to reaktancja wzajemna cewek.

Gdy cewki są nawinięte zgodnie tzn. zwrot prądu w obydwu cewkach jest jednakowo skierowany względem początku nawijania to znak indukcyjności wzajemnej M jest taki sam jak przy indukcyjności własnej L i dodaje się do każdej z cewek. Natomiast jeśli zwroty w obydwu cewkach są inaczej skierowane w stosunku do gwiazdek to znak przy indukcyjności M. jest przeciwny do znaku przy L. Obrazują to wykresy. Jak widać połącznie zgodne jak i przeciwne znacznie zmienia właściwości obu cewek a więc i całego układu. Jak widać wartość ta będzie na pewno mniejsza niż w przypadku sprzężenia zgodnego.

Przy takiej konfiguracji gdzie prąd nie płynął przez jedną z cewek można było traktować taki obwód jak układ symulujący transcormator w stanie jałowym. Pomiary wykazują, że napięcie jest indukowane na drugim uzwojeniu. Można było również policzyć współczynnik sprzężenia.

W ćwiczeniu należało dla sprzężenia przeciwnego dołączyć szeregowo do obwodu rezystancję, która ogranicza prąd przy małej impedancji wypadkowej cewek.

Można powiedzieć, że pomiary wykazują słuszność praw wyprowadzonych z teorii. Drobne odchyły od wyników teoretycznych można tłumaczyc klasą urządzeń pomiarowych lub czynnikiem ludzkim

---