N A P R Ę Ż E N I A P O D F U N D A M E N T E M B E Z P O Ś R E D N I M

Naprężenia pod fundamentem oblicza się w celu oceny spodziewanego osiadania

podłoża. Stan naprężeń w ośrodku gruntowym pod geometrycznym środkiem bezpośredniego,

prostokątnego fundamentu, posadowionego w wykopie zmienia się w trakcie realizacji

inwestycji.

1. Przed rozpoczęciem inwestycji w gruncie istnieją naprężenia pierwotne, których źródłem

jest ciężar własny gruntu

i

i

n

1

i

h

m

g

s

g

×

=

å

=

gdzie: h – głębokość od powierzchni terenu [m],

i – numer warstwy geotechnicznej,

n – ilość warstw geotechnicznych,

m

i

– miąższość kolejnej warstwy [m],

g

i

– ciężar objętościowy warstwy [kN/m

3

].

W przypadku, gdy warstwa geotechniczna znajduje się poniżej zwierciadła wody gruntowej

należy uwzględnić wypór wody działający na szkielet gruntowy i do obliczenia naprężeń

przyjąć ciężar objętościowy gruntu

g’ = (1 – n) (g

s

-

g

w

).

Dla przykładu przedstawionego na rysunku 1, naprężenia pierwotne w poziomie

posadowienia wynoszą:

1

γ

D

γ

D

×

=

s

naprężenia pierwotne na głębokości z poniżej poziomu posadowienia (głębokość h poniżej

powierzchni terenu) są równe:

(

)

'

γ

m

z

r

m

γ

D

2

1

1

1

1

r

h

×

-

+

×

+

×

=

s

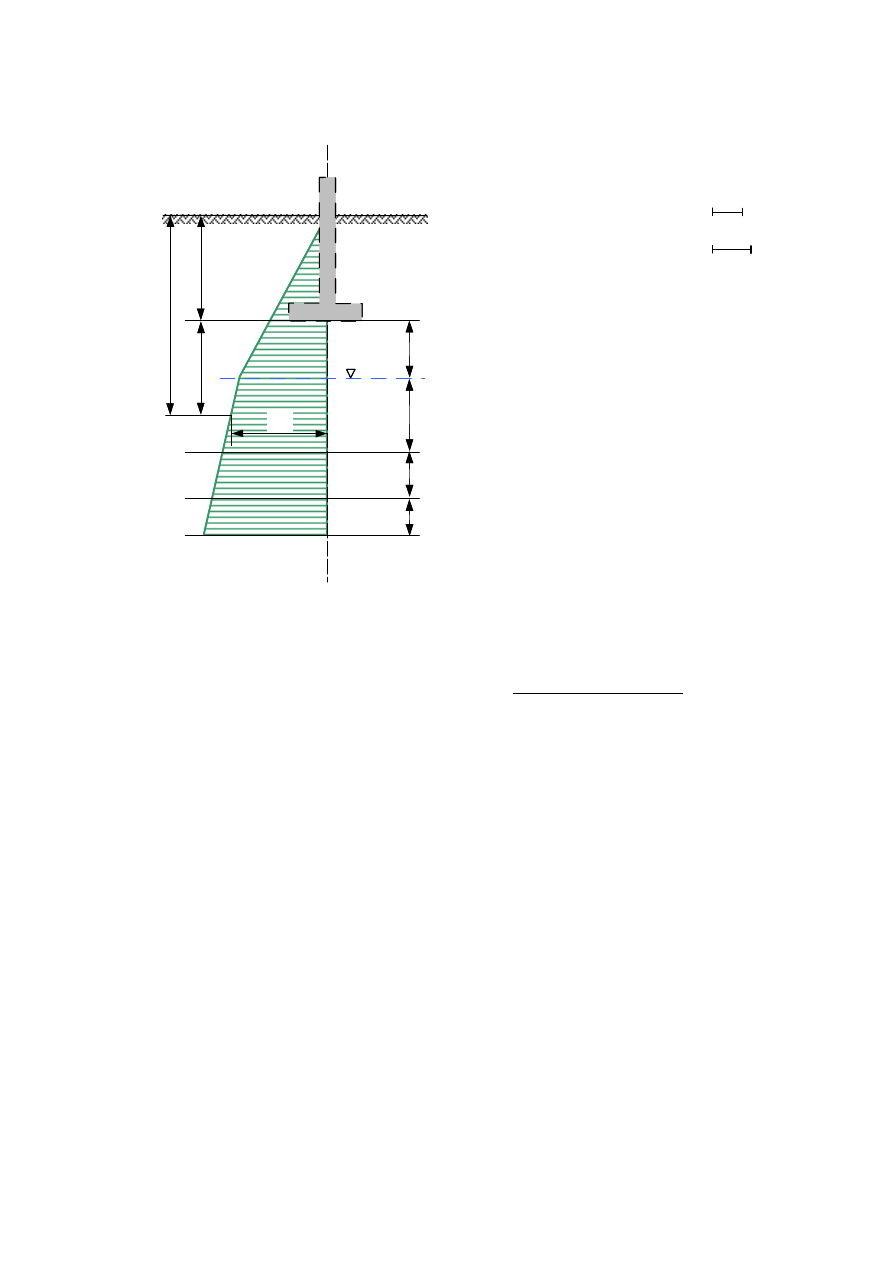
Rys. 1 Wykres naprężeń pierwotnych

2. Po wykonaniu wykopu fundamentowego następuje odprężenie gruntu i istniejące w tym

stanie naprężenia pionowe w gruncie noszą nazwę naprężeń minimalnych (rysunek 2).

Naprężenia minimalne w dnie wykopu są równe zero, zaś na głębokości z > 0 poniżej

poziomu posadowienia wynoszą:

s

z

h

m

z

-

s

s

s

g

=

gdzie:

m
z

σ - naprężenia minimalne [kPa],

g

h

σ - naprężenia pierwotne [kPa],

s

z

σ - naprężenia wtórne [kPa].

Naprężenia wtórne w poziomie posadowienia są równe naprężeniom pierwotnym na tym

poziomie:

g

s

s

D

s

0

z

=

=

Na głębokości z > 0 naprężenia wtórne oblicza się ze wzoru:

o

s

0

z

s

z

η

×

=

=

s

s

D

z

m

1

m

2

m

3

m

4

σ

h

γ

zwg

h

z = 0

Podziałka głębokości:

1 m

20 kPa

Podziałka naprężeń:

γ

1

γ

1

γ

4

'

γ

3

'

γ

2

'

D

z

m

1

m

2

m

3

m

4

zwg

h

z = 0

Podziałka głębokości:

1 m

20 kPa

Podziałka naprężeń:

γ

1

γ

1

γ

4

'

γ

3

'

γ

2

'

σ

h

γ

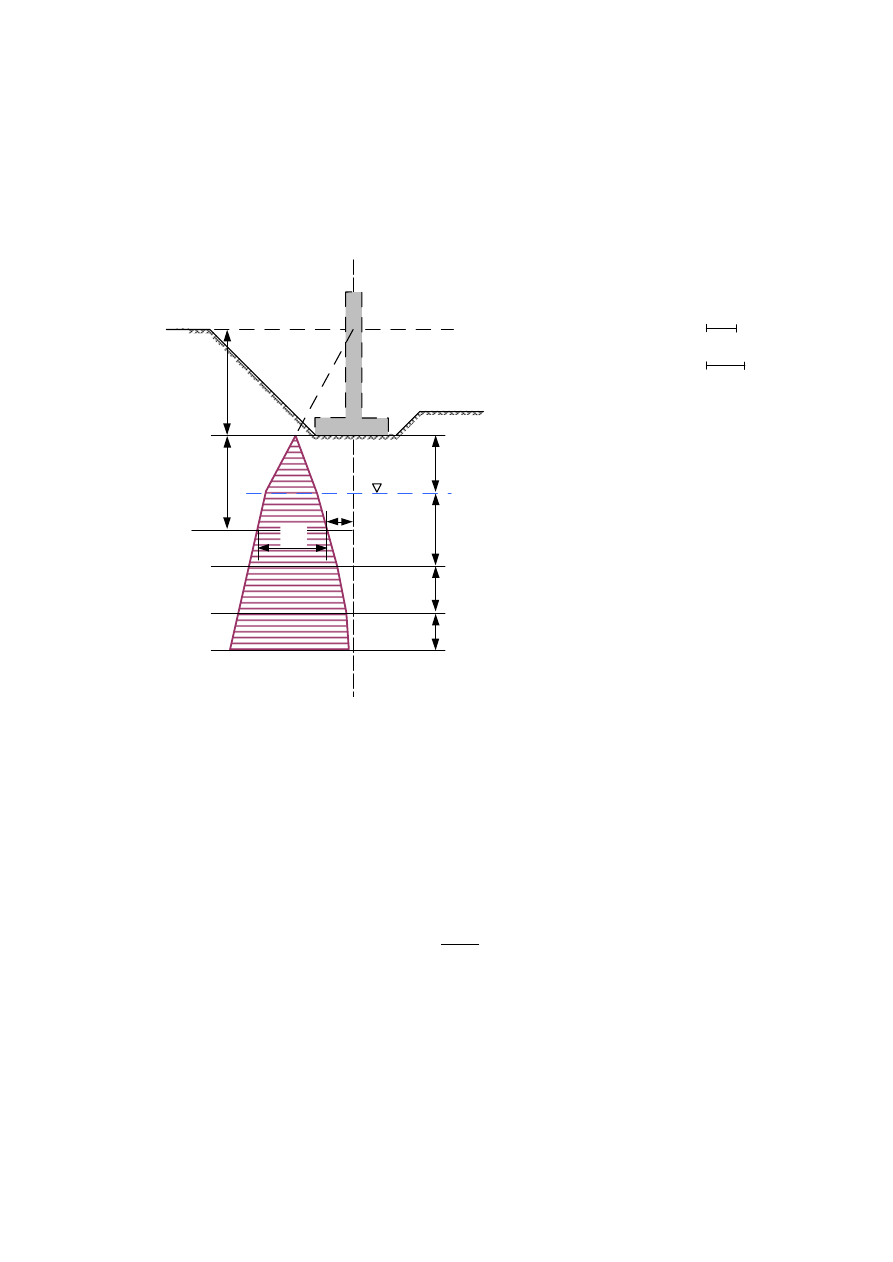
gdzie:

h

o

– współczynnik zanikania naprężeń dla metody punktów środkowych.

Rys. 2 Wykres naprężeń minimalnych

3. W dalszych etapach realizacji inwestycji siła Q, pochodząca od ciężaru fundamentu oraz

nadziemnych części obiektu budowlanego (ciężar ścian, stropów itd) systematycznie rośnie.

4. Po zakończeniu inwestycji i wyposażeniu obiektu jednostkowe obciążenie działające na

podłoże gruntowe wynosi:

B

L

Q

q

×

=

gdzie:

Q – obciążenie od fundamentu i budowli [kN],

L, B – wymiary fundamentu [m].

D

z

m

1

m

2

m

3

m

4

zwg

σ

z

s

Podziałka głębokości:

1 m

20 kPa

Podziałka naprężeń:

z = 0

σ

z

m

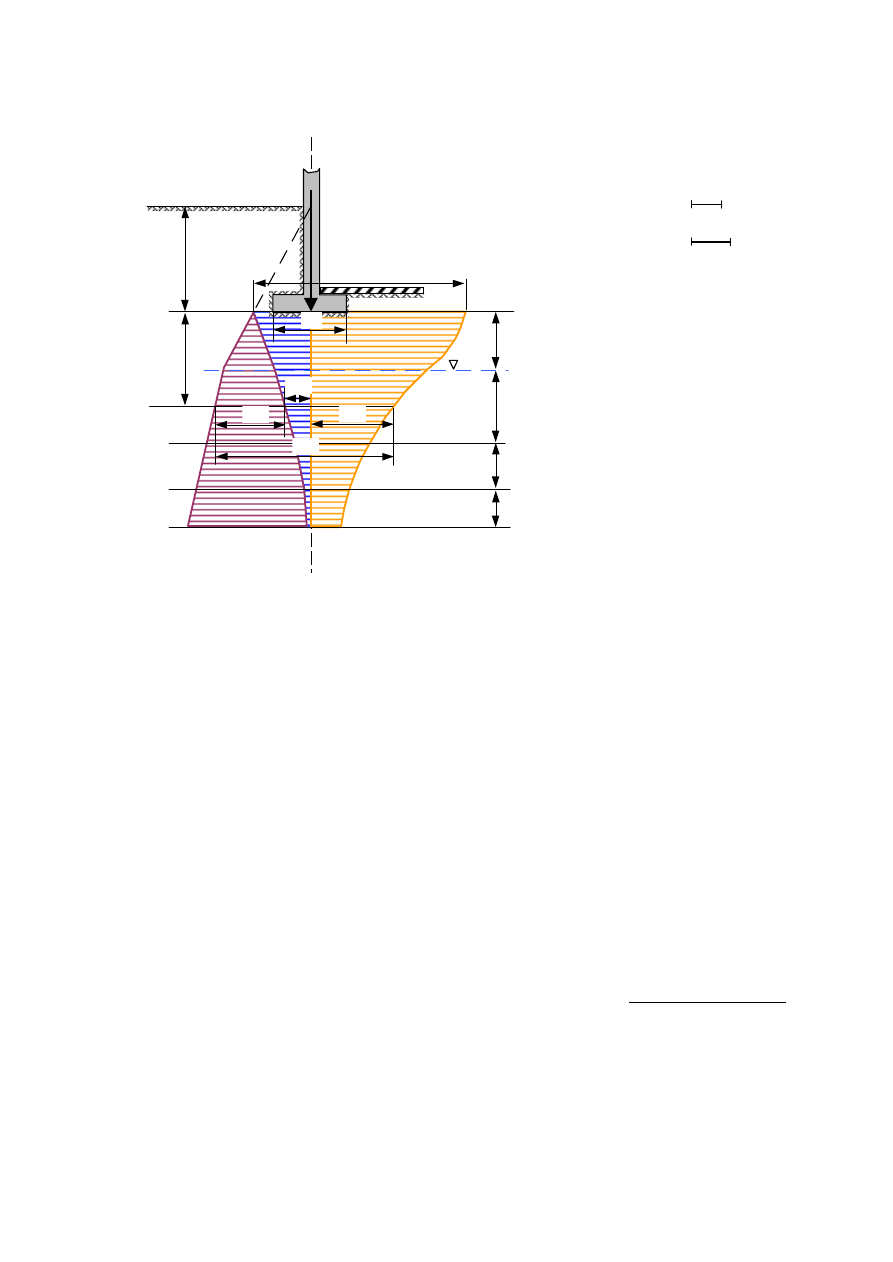
Rys 3. Wykres naprężeń wtórnych, dodatkowych i całkowitych

W poziomie posadowienia jednostkowe obciążenie podłoża q jest równe:

d

0

z

s

0

z

q

=

=

+

=

s

s

, czyli:

s

0

z

d

0

z

q

=

=

-

=

s

s

gdzie

s

0

z

=

s

- naprężenie wtórne [kPa],

d

0

z

=

s

- naprężenie dodatkowe [kPa].

Na głębokości z > 0 naprężenie dodatkowe oblicza się według wzoru:

o

d

0

z

d

z

h

s

s

×

=

=

Po oddaniu obiektu do eksploatacji w ośrodku gruntowym panują naprężenia całkowite

(rysunek 3), które oblicza się ze wzorów:

d

z

r

h

t

z

s

s

s

+

=

, lub

d

z

s

z

m

h

t

z

s

s

s

s

+

+

=

D

z

m

1

m

2

m

3

m

4

zwg

z = 0

q = Q/LB

Q

Podziałka głębokości:

1 m

20 kPa

Podziałka naprężeń:

σ

z

m

σ

z

s

σ

z

d

B

σ

z

t

W przypadku, gdy w pobliżu rozpatrywanego fundamentu znajduje się obiekt wywierający

nacisk na podłoże należy dodatkowo obliczyć naprężenia od tego obiektu, posługując się

metodą punktów narożnych.

Wykres naprężeń pod fundamentem należy sporządzić do głębokości z

max

, do której będą

obliczane osiadania podłoża.

Głębokość podłoża budowlanego z

max

wyznacza się według warunku:

g

s

s

z

d

max

z

3

.

0

£

Najprościej wartość z

max

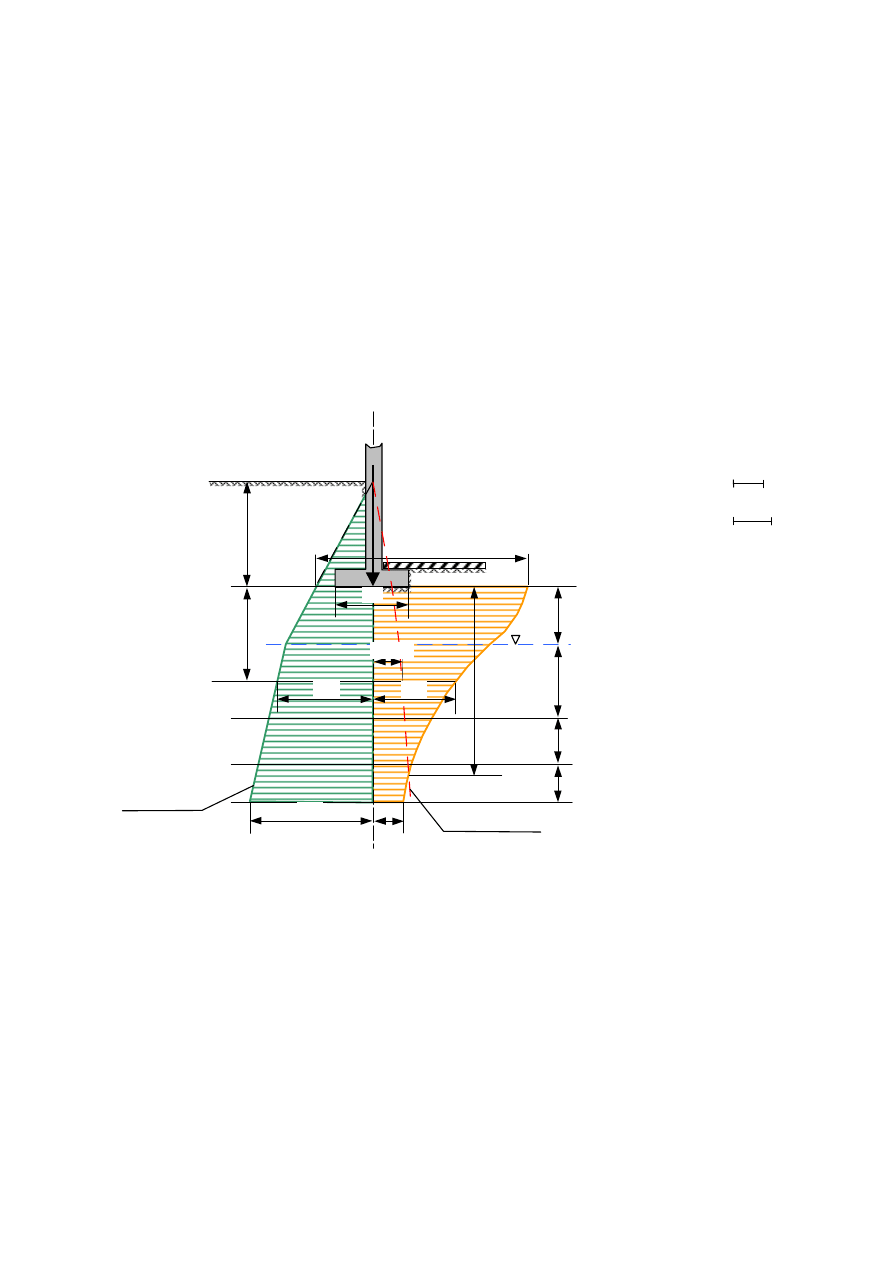
można wyznaczyć graficznie, stosując konstrukcję wykreślną jak na

rysunku 4.

Rys. 4 Wyznaczenie głębokości podłoża budowlanego (z

max)

Jeśli jednak głębokość z

max

wyznaczona graficznie wypadnie w obrębie warstwy

geotechnicznej „słabej”, o module ściśliwości pierwotnej M

o

co najmniej dwukrotnie

mniejszym niż w bezpośrednio głębiej zalegającej warstwie geotechnicznej, to głębokość

podłoża budowlanego ( z

max

) należy powiększyć do spągu tej warstwy.

D

z

m

1

m

2

m

3

m

4

zwg

z = 0

q = Q/LB

Q

Podziałka głębokości:

1 m

20 kPa

Podziałka naprężeń:

wykres naprężeń
pierwotnych

linia pomocnicza
0.3σ

h

γ

z

max

0.3σ

h

γ

σ

h

γ

σ

z

d

B

0.3σ

h

γ

σ

h

γ

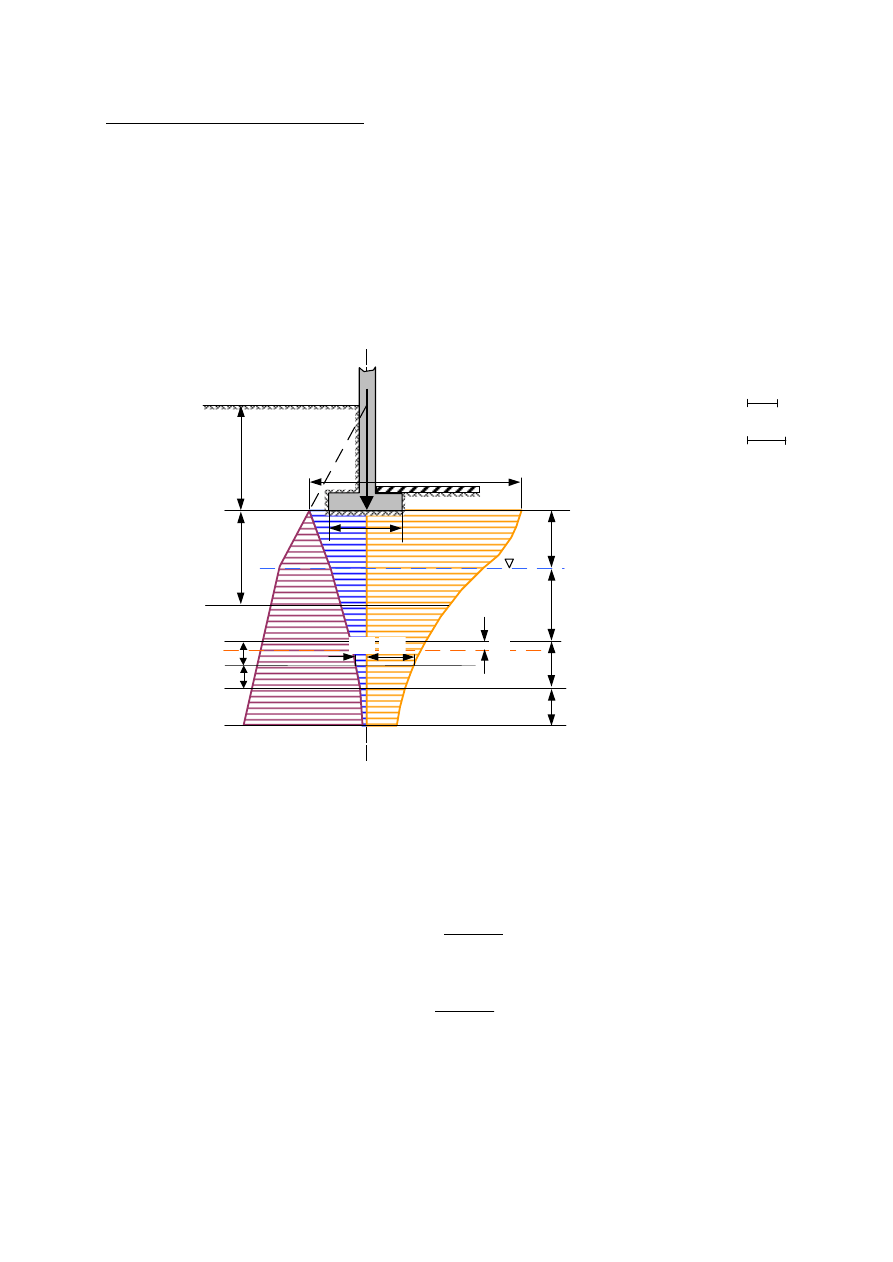
Obliczanie osiadania fundamentów.

Obliczanie osiadania zaleca się przeprowadzić metodą naprężeń. Osiadanie S

i

warstwy należy

wyznaczyć jako sumę osiadania wtórnego S

i

” w zakresie naprężenia wtórnego

s

z

s

, z

zastosowaniem modułu ściśliwości wtórnej gruntu M (lub modułu wtórnego odkształcenia E,

w zależności od metody obliczania), oraz osiadania pierwotnego S

i

’ w zakresie naprężenia

dodatkowego

s

z

d

, z zastosowaniem modułu ściśliwości pierwotnej gruntu M

o

(lub E

o

).

Rys. 5 Schemat obliczenia osiadania pojedyńczej warstwy podłoża

Osiadanie S

i

warstwy podłoża o miąższości m

i

oblicza się wg wzorów:

'

i

''

i

i

S

S

S

+

=

i

i

s

zi

''

i

M

m

S

×

=

s

l

oi

i

d

zi

'

i

M

m

S

×

=

s

w których:

"

i

S – osiadanie wtórne warstwy i, [cm],

'

i

S – osiadanie pierwotne warstwy i, [cm],

D

z

m

1

m

2

m

3

m

4

zwg

z = 0

q = Q/LB

Q

Podziałka głębokości:

1 m

20 kPa

Podziałka naprężeń:

m

3

/2

m

3

/2

σ

z3

s

σ

z3

d

B

S

3

d

zi

s

zi

,

s

s

– odpowiednio wtórne i dodatkowe naprężenie w podłożu pod fundamentem,

w połowie grubości warstwy, [kPa],

M

i

, M

oi

– edometryczny moduł ściśliwości, odpowiednio wtórnej i pierwotnej,

ustalony dla gruntu warstwy i, kPa,

m

i

– grubość warstwy i, cm,

l

- współczynnik uwzględniający stopień odprężenia podłoża po wykonaniu wykopu,

którego wartość należy przyjmować:

l

= 0 – gdy czas wznoszenia budowli (od wykonania wykopów fundamentowych do

zakończenia stanu surowego, z montażem urządzeń stanowiących obciążenie

stałe) nie trwa dłużej niż 1 rok,

l

= 1.0 – gdy czas wznoszenia budowli jest dłuższy niż 1 rok.

Warstwy o grubości większej niż połowa szerokości B fundamentu należy dzielić dodatkowo

na części o miąższości nie przekraczającej 0.5B.

Całkowite osiadanie podłoża pod fundamentem bezpośrednim, a zatem osiadanie całej

budowli oblicza się sumując osiadania wszystkich warstw cząstkowych według wzoru:

å

=

=

n

1

i

i

S

S

gdzie:

i – numer warstwy cząstkowej;

n – ilość warstw,

S

i

– osiadanie warstwy i–tej.