1

4

. OSCYLATOR HARMONICZNY PROSTY,

TŁUMIONY I WYMUSZONY. REZONANS.

1. PODSTAWOWE POJĘCIA

Ruch (drgania) harmoniczny (perjondyczny) – ruch powtarzający się w regularnych odstępach

czasu. Może być tłumiony, gdy jakaś zewnętrzna siła tłumi ruch powodując stopniowe zmniejszanie
się jego amplitudy lub też wymuszony, gdy zewnętrzna siła wymusza drgania.

Okres drgań T to czas trwania jednego pełnego cyklu (drgnięcia) – najkrótszy czas, po którym

ruch zaczyna się powtarzać.

Częstość drgań ν jest liczbą cyklów (drgań) na jednostkę czasu [Hz] – odwrotność okresu.

ν = T

-1

(1)

Amplituda – wartość bezwzględna maksymalnego wychylenia (przemieszczenia).
W ruchu harmonicznym siła działająca na punkt materialny w dowolnym jego położeniu zależy

od energii potencjalnej wg równania:

F = -dU/dx (2)

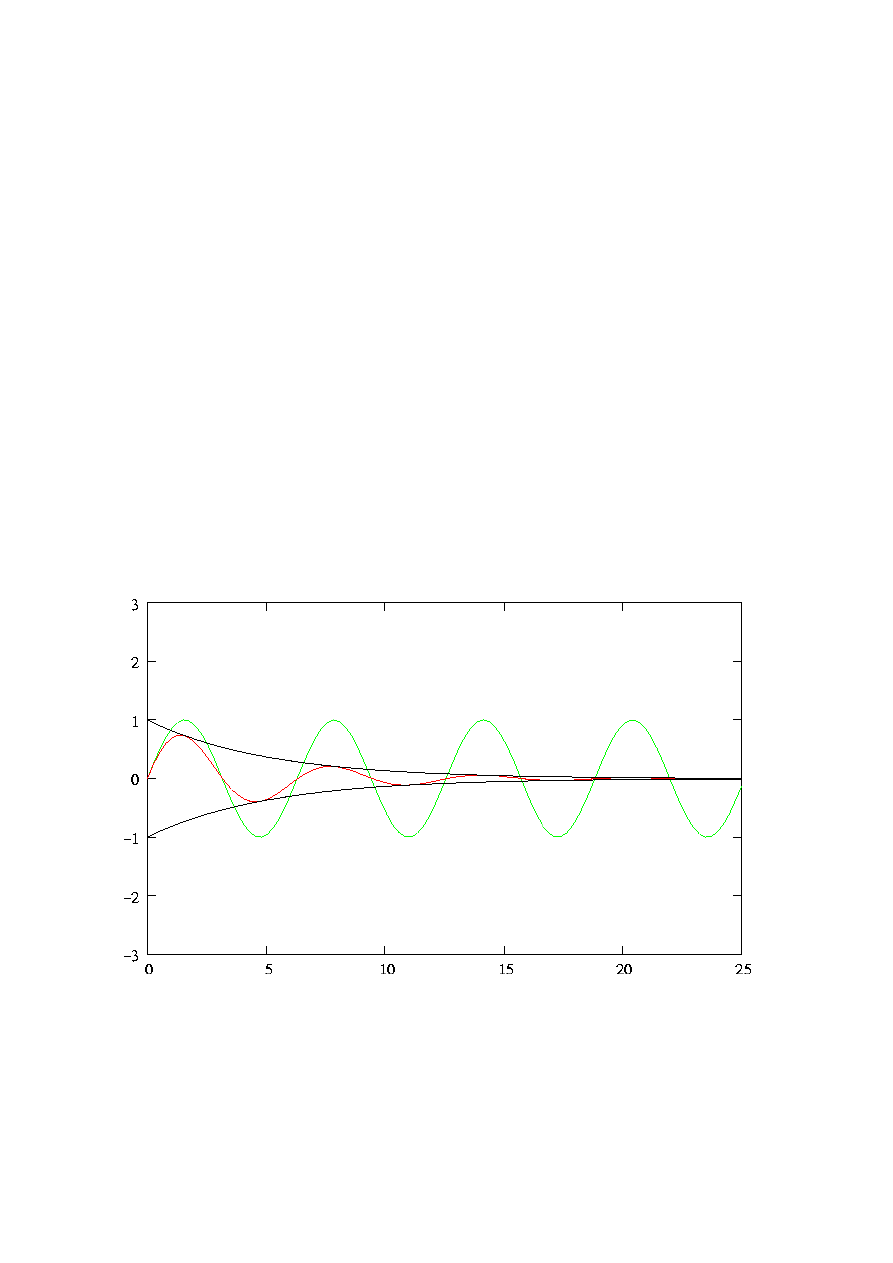
Rys. 1 – Położenie w ruchu harmonicznym nietłumionym (zielony), tłumionym (czerwony),

obwiednia ruchu tłumionego (czarny). [Wikipedia]

Skupiłem się na drganiach na przykładzie wahadeł.

Oscylacje na poziomie atomowym pewnie pojawią się w modelach atomu.

Jak nie to jeszcze to uzupełnię.

2

2. OSCYLATOR HARMONICZNY PROSTY

Energia potencjalna punktu materialnego poruszającego się w tą o z powrotem wokół punktu

równowagi można opisać wzorem:

U(x) = ½ k x

2

(3)

gdzie k to tzw. współczynnik sprężystości określający jak szybko następuje powrót do stanu

równowagi.

Natomiast siła działająca na omawiany punkt (wg równania 2):

F(x) = -k x (4)

– zależność znana jako prawo Hook’a.
Z drugiej zasady Newtona możemy wyprowadzić równanie ruchu (różniczkowe) oscylatora

harmonicznego prostego:

0

2

2

2

2

=

+

=

−

x

m

k

dt

x

d

dt

x

d

m

kx

(5)

Przekształćmy je do postaci:

x

m

k

dt

x

d

−

=

2

2

(6)

Widać teraz, że rozwiązaniem x(t) równania jest funkcja, której druga pochodna jest równa jej

samej ze stałym współczynnikiem k/m i o przeciwnym znaku. Przyjmijmy więc rozwiązanie próbne:

(

)

ϕ

ω

+

=

t

A

x

(7)

Po podwójnym zróżniczkowaniu otrzymamy:

(

)

ϕ

ω

ω

+

−

=

t

a

dt

dx

cos

2

2

2

(8)

co po przyrównaniu do wzoru 6 daje zależność:

m

k

=

2

ω

(9)

Okres ruchu

T równy jest

ω

π

/

2

, co po podstawieniu da nam:

k

m

T

π

ω

π

2

2 =

=

(10)

ω jest więc częstością kołową (kątową) o wymiarze s

-1

i jednostce rad/s.

A to oczywiście amplituda.

Czynnik

(

)

ϕ

ω

+

t

nazywamy fazą ruchu, a

ϕ

– fazą początkową.

3

Rozważmy zależność przemieszczenia, prędkości i przyspieszenia od czasu:

(

)

(

)

(

)

ϕ

ω

ω

ϕ

ω

ω

ϕ

ω

+

−

=

=

+

−

=

=

+

=

t

A

a

t

A

v

t

a

x

dt

dv

dt

dx

cos

sin

cos

2

(11)

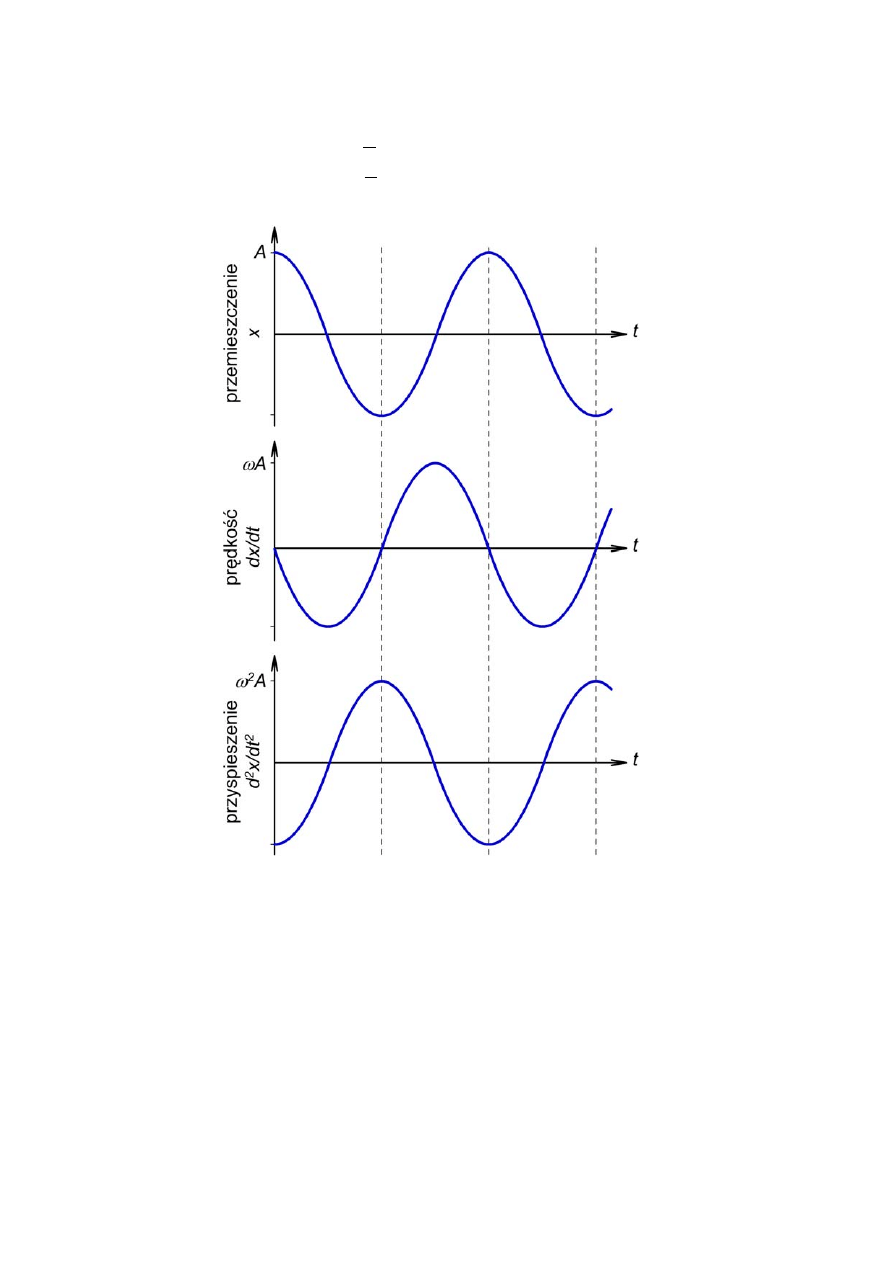
Rys. 2 – Zależność przemieszczenia, prędkości i przyspieszenia od czasu w ruchu harmonicznym prostym.

Na przykład przy maksymalnym wychyleniu prędkość jest zerowa, ponieważ ruch zmienia

kierunek, a przyspieszenie (tak jak siła przywracająca równowagę) osiąga wartość maksymalną, ale
jest skierowana przeciwnie do przemieszczenia.

4

3. UKŁADY FIZYCZNE Z RUCHEM HARMONICZNYM PROSTYM

Wahadło proste (matematyczne)
Ciało na nieważkiej, nierozciągliwej nici o długości l i punktowej masie m. Siła przywracająca

równowagę układu: F = -mg sinθ.

Dla małych wychyleń sinθ ≈ θ, a przemieszczenie x = lθ. Wtedy:

x

l

mg

l

x

mg

mg

F

−

=

−

=

−

=

θ

(12)

a przez analogię do wzoru 4 – okres wahadła opiszemy wzorem:

g

l

l

mg

m

k

m

T

π

π

π

2

/

2

2

=

=

=

(13)

Znając okres wahadła matematycznego możemy wyznaczyć przyspieszenie ziemskie:

2

2

4

T

l

g

π

=

Wahadło torsyjne
Krążek zawieszony w środku masy na sztywno zamocowanym drucie. Moment siły

przywracający wahadło ze skręcenia do stanu równowagi:

χθ

τ

−

=

, gdzie

χ jest stałą skręcenia

(inaczej momentem kierującym).

Równanie ruchu:

2

2

dt

d

I

dt

d

I

I

θ

ω

α

τ

=

=

=

, gdzie

α – przyspieszenie kątowe; ω – prędkość kątowa;

θ – kąt wychylenia, a I – moment bezwładności krążka.

Po podstawieniu do poprzedniego równania otrzymamy:

θ

χ

θ

θ

χθ

I

dt

d

dt

d

I

−

=

→

=

−

2

2

2

2

(14)

Widać już analogię do liniowego ruchu harmonicznego prostego. Zamiast parametrów liniowych

są kątowe, zamiast

k jest χ.

Okres drgań wyrazi sie więc wzorem:

χ

π

I

T

2

=

(15)

Wahadło fizyczne
Dowolne ciało sztywne wahające się wzdłuż pewnej osi przechodzącej przez to ciało.

Rozważmy przypadek 2D. Podobnie jak poprzednio dla małych amplitud:

χθ

θ

τ

−

=

−

= Mgd

,

gdzie d – odległość między osią obrotu a środkiem masy ciała. Równanie ruchu i okres drgań jest
podobny jak dla wahadła torsyjnego.

Oczywiście w ogólnym przypadku mamy do czynienia z ciałem o dowolnym kształcie

zawieszonym na dowolnej osi!

5

4. OSCYLATOR HARMONICZNY TŁUMIONY

Istnieje zewnętrzna siła (np. siła tarcia) zmniejszająca amplitudę drgań. Siła ta jest zależna od

prędkości drgań. Dla prostego oscylatora harmonicznego tłumionego równanie ruchu wygląda
następująco:

0

2

2

=

+

+

kx

dt

dx

b

dt

x

d

m

(16)

W porównaniu do równania oscylatora nietłumionego pojawiła się siłą tłumiąca proporcjonalna

do prędkości drgań.

Jeżeli stała

b jest mała (na tyle, że układ nie powraca od razu do stanu równowagi tylko wykonuje

kilka wahnięć), to rozwiązanie równania wygląda następująco:

(

)

ϕ

ω

+

=

−

t

Ae

x

m

bt

'

cos

2

/

(17)

gdzie

2

2

'

2

'

⎟

⎠

⎞

⎜

⎝

⎛

−

=

=

m

b

m

k

πυ

ω

Amplituda drgań maleje eksponencjalnie do zera (czerwona linia na rys. 1).
Logarytmiczny dekrement tłumienia

– logarytm naturalny ze stosunku dwóch kolejnych

wartości amplitud w odstępie czasu równym okresowi drgań. Jest to parametr bezwymiarowy
określający szybkość zaniku drgań.

(

)

bT

e

Ae

Ae

bT

T

t

b

bt

=

=

=

+

−

−

ln

ln

δ

(18)

5. OSCYLATOR HARMONICZNY WYMUSZONY, REZONANS

Oprócz siły przywracającej układ do stanu równowagi i siły wymuszającej istnieje dodatkowa

okresowa siła zewnętrzna. W prostym przypadku siłę tą można opisać wzorem:

( )

t

F

m

''

cos

ω

, gdzie F

m

jest maksymalną wartością siły, a

''

ω

jej częstością kołową. Otrzymujemy więc równanie:

( )

t

F

kx

dt

dx

b

dt

x

d

m

m

''

cos

2

2

ω

=

+

+

(19)

Rozwiązaniem równania 19 jest:

(

)

ϕ

ω

−

=

t

G

F

x

m

''

sin

(20)

gdzie

(

)

2

2

2

2

2

2

''

''

ω

ω

ω

b

m

G

+

−

=

, a

G

b

''

arccos

ω

ϕ

=

Widać, że układ drga z częstością siły wymuszającej, a nie częstością własną. Gdy częstość siły

wymuszającej zbliży się do częstości własnej układu

ω

ω

→

''

, to

0

→

G

, a więc

∞

→

G

F

m

/

i amplituda rośnie do nieskończoności.

Oczywiście w rzeczywistości siła tłumiąca nie pozwoli na nieskończoną amplitudę drgań.

Osiągną one jednak maksymalną amplitudę – układ będzie w stanie rezonansu. Im słabsza jest siłą
tłumiąca, tym częstość rezonansowa (częstość siły wymuszającej, przy której następuje rezonans) jest
bliższa częstości drgać własnych układu.

Wyprowadzenia wzorów 17 i 20 znajdziecie w:
W. Rubinowicz, W. Królikowski, Mechanika teoretyczna, PWN, Warszawa 1978