1

11. Prąd elektryczny i prawa rządzące jego przepływem. 

 
Prądem elektrycznym nazywamy wszelki uporządkowany ruch ładunków elektrycznych w 
przestrzeni.  
Nośnikami prądu elektrycznego mogą być elektrony, jony bądź dziury, czyli puste miejsca po 
elektronach. W metalach swobodnie przemieszczają się jedynie elektrony, dlatego prąd elektryczny w 
metalach jest ruchem elektronów przewodnictwa. W półprzewodnikach nośnikami prądu są elektrony 
i dziury. W rozrzedzonych gazach nośnikami ładunku elektrycznego są elektrony i jony. 
Przepływem prądu rządzi szereg praw.  

 

Prawo Ohma 

Rozważmy sytuację, gdy do przewodnika (lub jego fragmentu) przyłożymy różnicę potencjałów U. 
Popłynie wówczas przezeń prąd o natężeniu I 4. Na początku XIX wieku Georg Ohm stwierdził, że 
natężenie prądu w metalach jest proporcjonalne do przyłożonego napięcia — o ile w trakcie pomiarów 
utrzymuje się stałą temperaturę metalowej próbki. 

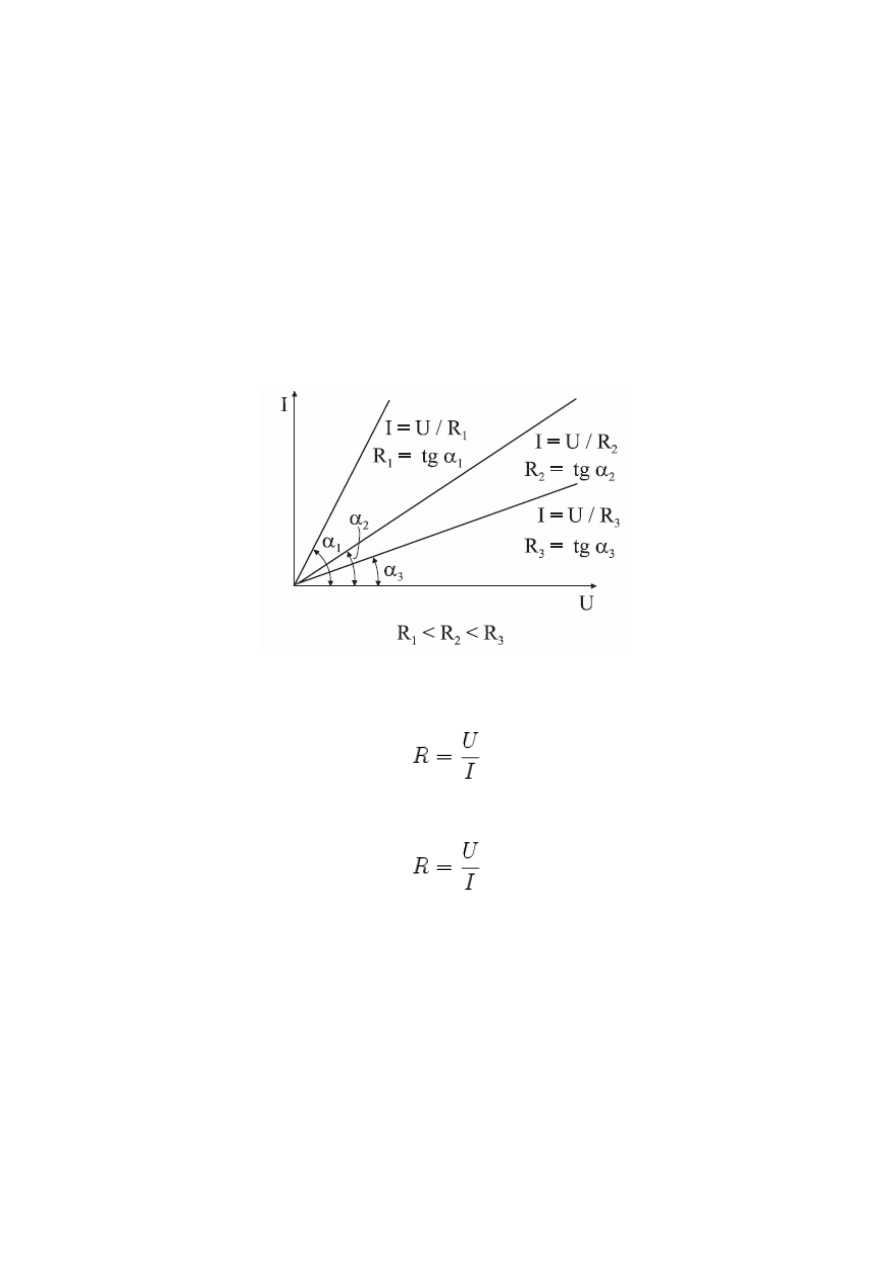
Zależność I(U) przedstawia rysunek 11.1 

 

Rys 11.1 . Zależność I(U) dla różnych wartości U 

 

Jak wynika z rysunku, nachylenie prostej zależy od wartości współczynnika 1/R. Wielkość R, 
zdefiniowana przez Ohma przy pomocy równania 

 

nosi nazwę oporu (rezystancji) przewodnika. Jednostką oporu jest 1 om (Ω), przy czym [Ω]=V/A. 
Podkreślamy,  że powyższe równanie jest definicją oporu, co oznaczyliśmy używając symbolu „≡”. 
Prawem Ohma jest natomiast stwierdzenie: w stałej temperaturze stosunek 

 

jest niezależny od natężenia prądu I. 
Oznacza to, że dany przewodnik spełnia prawo Ohma jeśli jego wykres I(U) jest liniowy, tzn. jeżeli 
jego opór R nie zależy od przyłożonego napięcia U i natężenia płynącego przezeń prądu I 
(podkreślmy jeszcze raz — przy zachowaniu stałej temperatury) 
Wiele przewodników prądu nie spełnia prawa Ohma. Należą do nich np. lampa elektronowa — dioda 
oraz elektrolity 
 
Opór jednorodnego przewodnika o stałym przekroju jest proporcjonalny do jego długości  l i 
odwrotnie proporcjonalny do powierzchni przekroju poprzecznego S:  

R = ς l/S 

W tym równaniu współczynnik proporcjonalności  ς nazywa się  oporem właściwym substancji, z 
której wykonany jest przewodnik. Wielkość odwrotna  

σ = 1/ς 

nazywa się przewodnictwem właściwym 

 

2

Ze wzrostem temperatury opór metali rośnie, natomiast półprzewodników i elektrolitów maleje. 
Własność  tę opisuje tzw. temperaturowy współczynnik oporu właściwego  α, wyrażający względną 
zmianę oporu właściwego przypadająca na jednostkową zmianę temperatury 

dT

dp

ρ

α

1

=

 

(jednostka [α]= 1/ ◦C). Jego wartość wynosi od np. 600·10

−5

 ◦C

−1

 dla niklu, 380 · 10

−5

 ◦C

−1

 dla srebra 

do 300 · 10

−5

 ◦C

−1

 dla stali. 

 

Prawo Joule’a – Lenza 

Przy przepływie prądu przez przewodnik zachodzi ciągłe, nieodwracalne przekształcanie energii 
prądu elektrycznego w energię wewnętrzną przewodnika. Praca przemieszczania energii przewodnika 
(i przepływ ciepła do otoczenia) Q: Q = W = qU, gdzie q jest ładunkiem przepływającym przez 
przekrój poprzeczny przewodnika w czasie t; q = it. Zatem:  

Q = iUt 

Wzór ten można przedstawić jeszcze inaczej, korzystając z prawa Ohma:  

Q = i

2

Rt = U

2

t/R 

Wzór w tej postaci nosi nazwę prawa Joule'a - Lenza  
Praca wykonana przez prąd w jednostce czasu, czyli moc wynosi: P = Q/t, zatem: 

P= iU 

 

Pierwsze prawo Kirchhoffa  

I prawo Kirchhoffa odnosi się do sytuacji gdy prąd płynący w jakimś układzie ulega rozgałęzieniu, 
czyli gdy przewody z prądem łączą się w jakimś punkcie.. 
Ponieważ  ładunki elektryczne nie mogą znikać, ani powstawać z niczego, a standardowy 
przewodnik właściwie nie potrafi ich gromadzić (wyjątkiem są kondensatory), to jasne jest, że: 
Jeśli w jakimś czasie do rozgałęzienia dopłynął  ładunek q, to w tym samym czasie z tego 
rozgałęzienia musiał również taki sam ładunek q odpłynąć. 
Ponieważ jednak ładunek wpływający, czy wypływający w jednostce czasu to nic innego jak 
natężenie prądu I, więc prawo to można sformułować odwołując się do tego pojęcia natężenia prądu: 
Suma natężeń prądów wpływających do rozgałęzienia, równa jest sumie natężeń prądów 
wypływających z tego rozgałęzienia. 
Powyższe prawo można zapisać wzorem: 

Σ I

wpływające

 = Σ I

wypływające

 

Drugie prawo Kirchhoffa  

Prawo to, zwane również prawem napięciowym, dotyczy bilansu napięć w zamkniętym obwodzie 
elektrycznym i jest swoistym uogólnieniem prawa Ohma w odniesieniu do rozgałęzionych sieci 
elektrycznych. Formułujemy je następująco 
W dowolnym obwodzie zamkniętym, wydzielonym w rozgałęzionej sieci, suma algebraiczna iloczynów 
natężeń prądów I

k

  i oporów R

k

 poszczególnych odcinków obwodu równa się sumie algebraicznej 

działających w nim sił elektromotorycznych             

∑

∑

=

k

k

k

k

k

R

I

ε

 

 

W celu zestawienia powyższego równania należy umownie przyjąć kierunek obiegu prądu. Wybór 
tego kierunku jest całkowicie dowolny. Wszystkie prądy o natężeniu I

k

, których kierunek jest zgodny 

z kierunkiem obiegu obwodu przyjmujemy jako dodatnie(w przeciwnym wypadku za ujemne)  Siły 
elektromotoryczne 

k

ε

  źródeł prądu, włączonych w różne odcinki obwodu, uważamy za dodatnie 

wówczas, gdy wytwarzany przez nie prąd jest zgodny z kierunkiem obiegu obwodu.