Wytrzymałość Materiałów, r.II, sem.III, wykład 6.

Jan Bielski

1

WYTRZYMAŁOŚĆ

MATERIAŁÓW

ROK STUDIÓW II

SEMESTR III

wykład 6

2

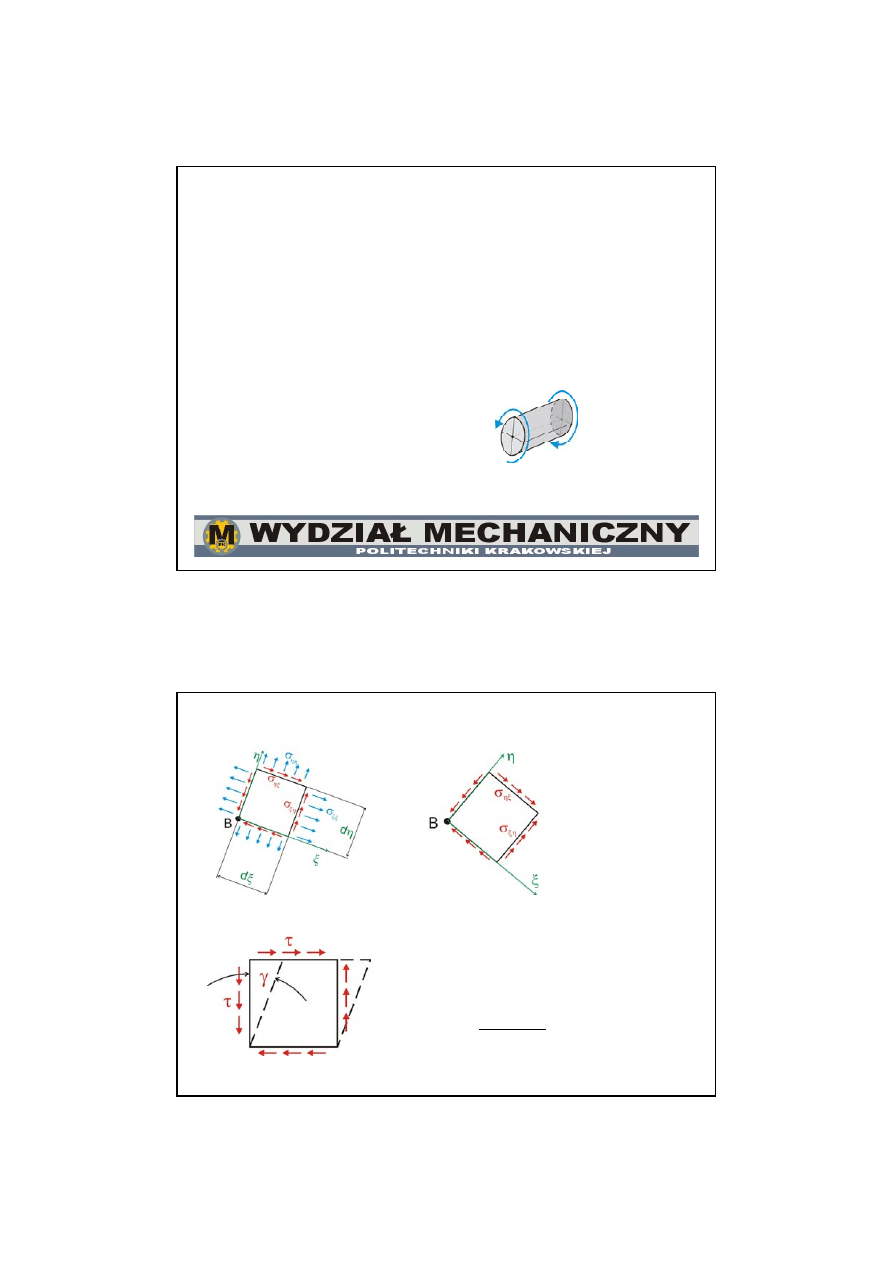
Czyste ścinanie

istnieje taki układ (

x,h),

że naprężenia normalne
są równe zero

0

0

=

-

Þ

=

å

x

h

s

h

x

s

xh

hx

d

d

d

d

M

B

xh

hx

s

s =

odkształcenia postaciowe;
brak odkształceń wzdłużnych

Wytrzymałość Materiałów, r.II, sem.III, wykład 6.

Jan Bielski

2

3

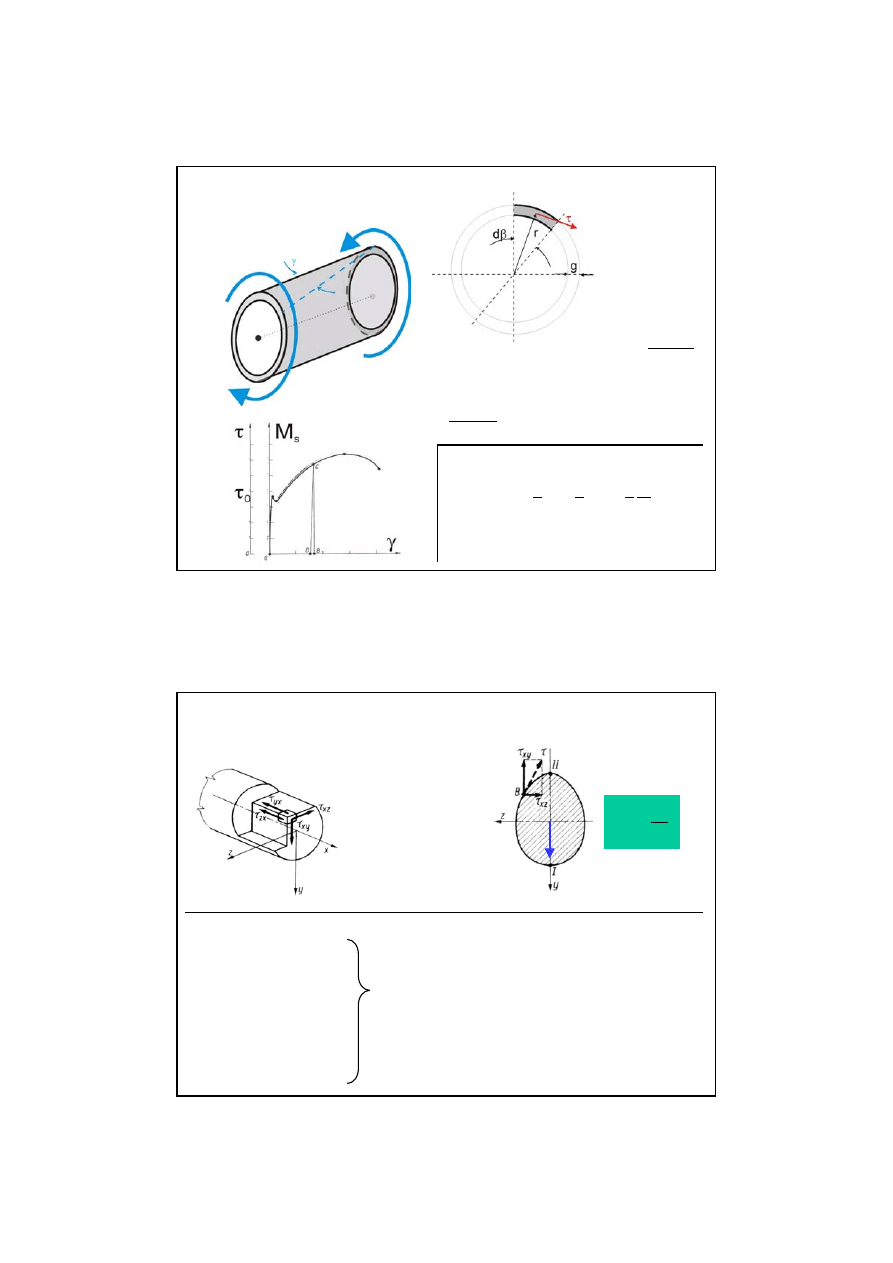
Próba wytrzymałościowa -
wyznaczenie zależności

t(g)

S

dM

r

g

d

r

=

b

t

t

p

b

t

p

g

r

d

g

r

M

S

2

2

0

2

2

=

=

ò

g

r

M

S
2

2

p

t =

g

t G

=

(

)

n

+

=

1

2

E

G

moduł Kirchhoff’a
(odkształceń postaciowych)

energia ścinania

( )

ò

=

F

g

g

g

t

0

d

G

G

e

2

2

2

1

2

1

2

1

t

g

g

t

=

=

=

F

òòò

F

=

)

(V

dV

L

4

Ścięcie techniczne

T

¹0 Þ t ¹0

( T

¹0, M

g

»0, N=0, M

s

=0 )

òò

=

)

( A

xy

dA

T

t

0

)

(

=

òò

A

xz

dA

t

(

)

òò

=

-

)

(

0

A

xz

xy

dA

y

z

t

t

A

T

sr

=

t

średnie naprężenie

styczne

• sworznie

• nity

• wpusty

• spoiny

• blachy cięte nożycami

• …...

elementy niszczące się przez ścięcie

Nie ma przekrojów dostatecznie odległych od miejsc
przyłożenia sił - nie da się zastosować zasady
de Saint Venant’a

Wytrzymałość Materiałów, r.II, sem.III, wykład 6.

Jan Bielski

3

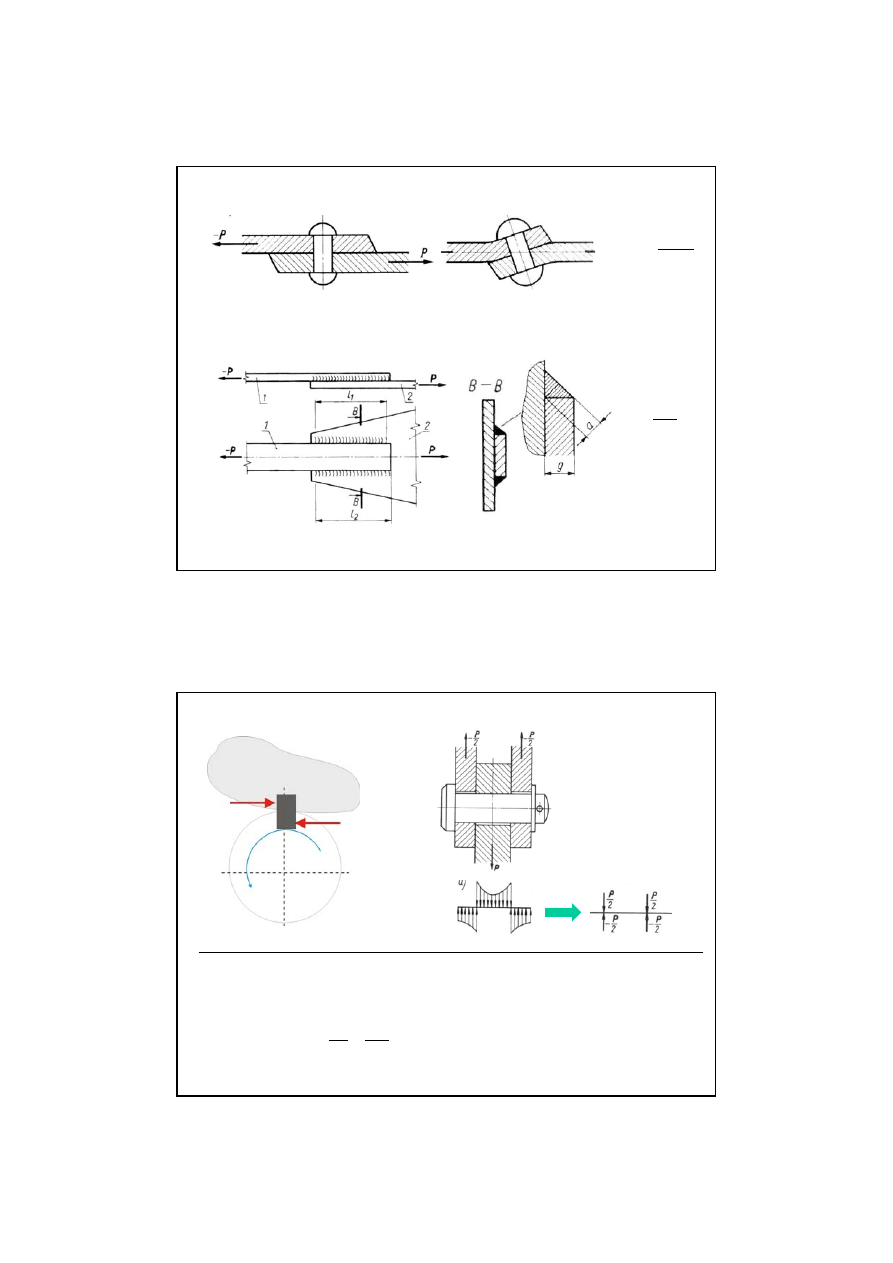
5

nit

sr

l

A

T

=

t

1

l

a

T

sr

=

t

nit

spoina

6

t

sr

k

£

t

warunek bezpieczeństwa
(nie liczymy odkształceń i przemieszczeń)

j

A

T

j

K

k

kr

t

t

=

=

wpust

sworzeń

r

t

k

k

58

.

0

5

.

0

×

»

¸

Wytrzymałość Materiałów, r.II, sem.III, wykład 6.

Jan Bielski

4

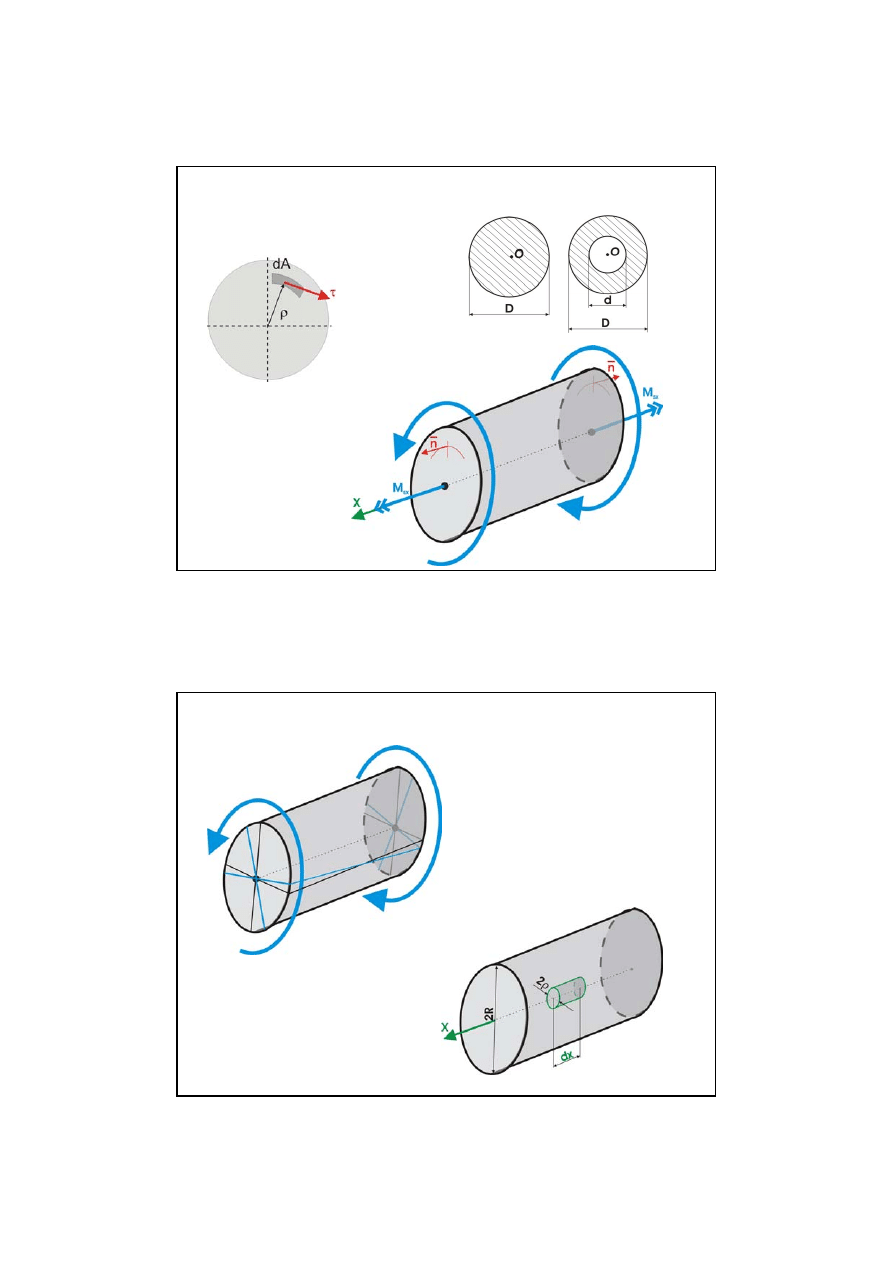
7

Skręcanie prętów o przekrojach kołowo symetrycznych

( M

s

¹0, N=0, T=0, M

g

=0 )

( )

r

r

t

dA

dM

S

=

( )

dA

M

A

S

r

r

t

òò

=

)

(

8

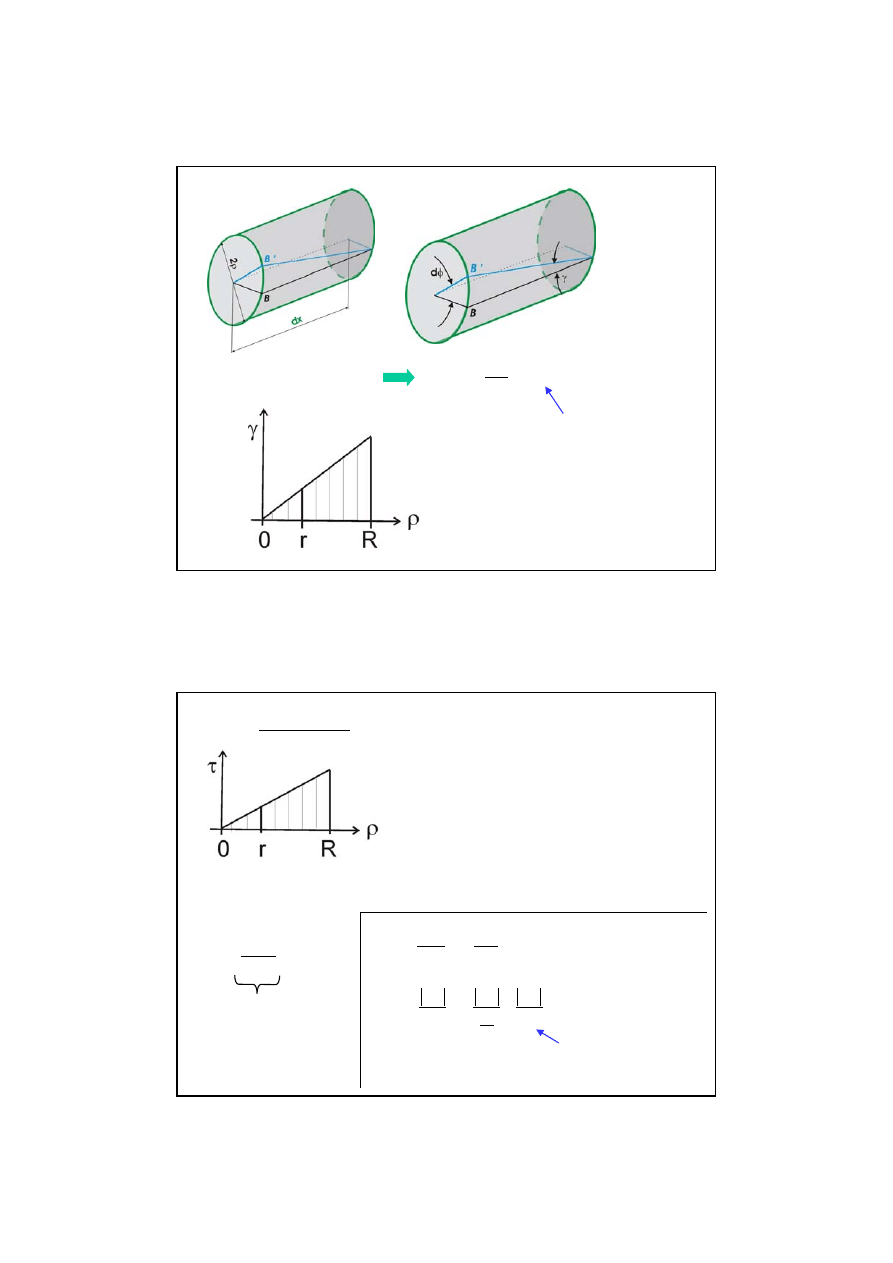
Analiza deformacji

hipoteza

Bernoulli’ego

• przekroje pozostają płaskie (nie ulegają
deplanacji), a jedynie obracają się
względem siebie

• prostoliniowy odcinek promieniowy
pozostaje prosty, o nie zmienionej
długości, obracając się wokół osi
skręcania

0 (r)

£r £R

Wytrzymałość Materiałów, r.II, sem.III, wykład 6.

Jan Bielski

5

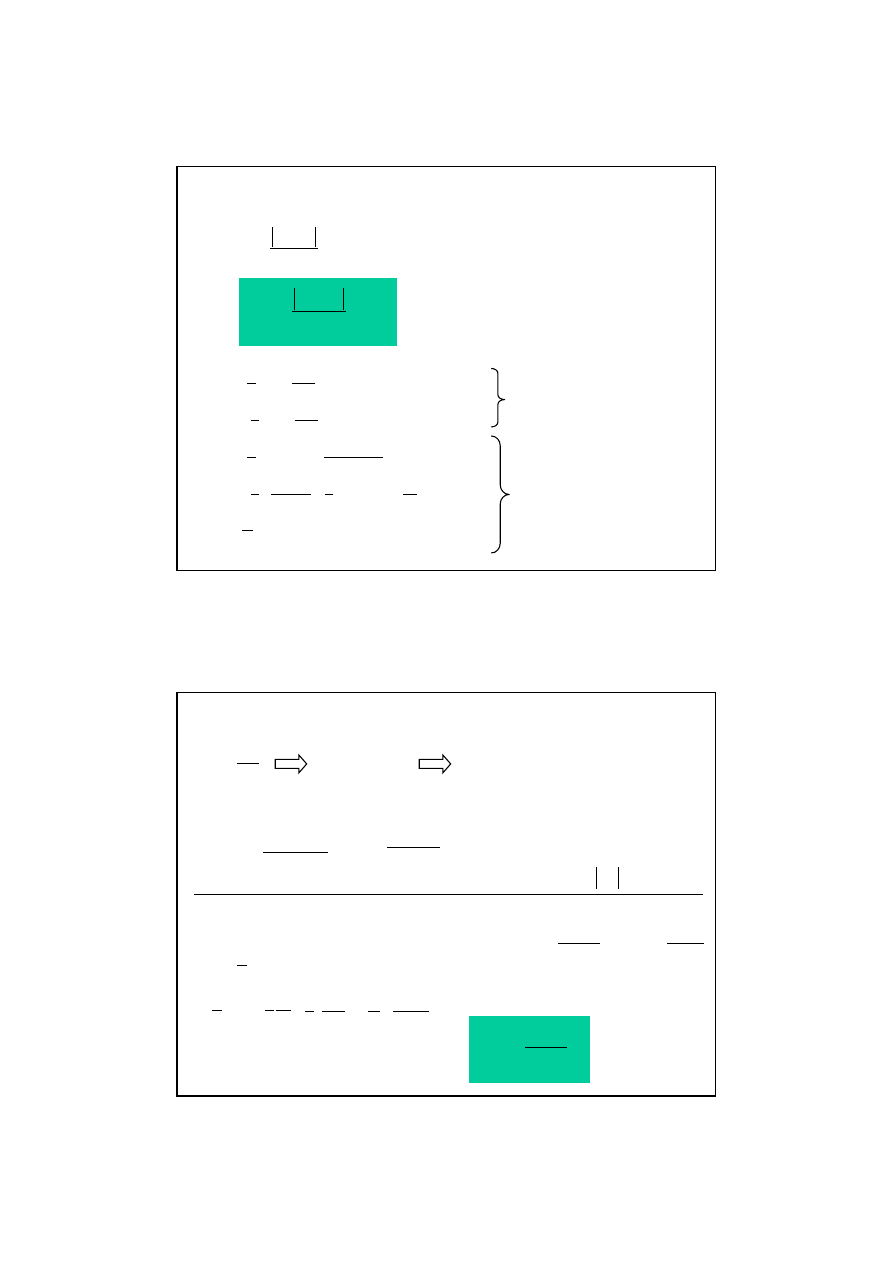
9

( )

dx

d

r

g

j

r

=

( )

u

r

j

r

r

g

=

=

dx

d

jednostkowy (właściwy)
kąt skręcenia

niezależnie od prawa
fizycznego (materiału)

10

materiał liniowo sprężysty

t

max

g

t G

=

r

u

G

=

R

G

u

t

=

max

( )

dA

M

A

S

r

r

t

òò

=

)

(

0

2

)

(

I

G

dA

G

A

u

r

u

=

=

òò

I

0

- biegunowy

moment
bezwładności
przekroju

0

I

G

M

S

u

=

0

I

G

M

S

=

u

sztywność skrętna przekroju

r

r

t

0

0

I

M

I

G

M

G

S

S

=

=

0

0

0

max

W

M

R

I

M

R

I

M

S

S

S

=

=

=

t

wskaźnik skręcania
przekroju

Wytrzymałość Materiałów, r.II, sem.III, wykład 6.

Jan Bielski

6

11

warunek bezpieczeństwa

( )

( )

( )

x

W

x

M

x

S

0

max

=

t

(

)

)

(

max

)

(

:

max

0

max

0

x

x

x

x

t

t

=

$

przekrój niebezpieczny

( )

( )

S

S

x

k

x

W

x

M

£

þ

ý

ü

î

í

ì

0

max

( )

{

}

0

max

max

t

t

=

x

x

warunek nośności sprężystej

(

) (

)

(

)

(

)

R

r

s

s

D

s

R

R

r

R

W

d

D

r

R

I

D

R

W

D

R

I

=

-

=

-

=

-

=

-

=

-

=

=

=

=

=

4

3

4

3

4

4

0

4

4

4

4

0

3

3

0

4

4

0

1

16

1

1

2

1

2

1

32

2

1

16

2

1

32

2

1

p

p

p

p

p

p

p

p

p

pełny przekrój kołowy

przekrój drążony (pierścieniowy)

12

kąt skręcenia wałka

dx

d

j

u =

dx

d

u

j =

( )

ò

=

2

1

2

1

x

x

x

x

dx

x

u

j

kąt obrotu przekroju o
współrzędnej x

2

względem przekroju o
współrzędnej x

1

( )

ò

=

)

( L

C

dx

x

u

j

całkowity kąt skręcenia wałka

dla pręta sprężystego

( )

( )( )

ò

=

)

(

0

L

S

C

dx

x

I

G

x

M

j

max

min

j

j

j

£

£

C

warunek sztywności

energia sprężystej deformacji

g

t

2

1

=

F

e

gęstość energii w punkcie

G

G

2

2

2

1

2

1

t

g =

=

2

2

0

2

2

0

2

1

2

1

r

r

I

G

M

G

I

G

M

S

S

=

÷÷ø

ö

ççè

æ

=

0

2

)

(

2

2

0

2

)

(

)

(

2

2

I

G

M

dA

I

G

M

dA

L

S

A

S

A

e

e

A

=

=

F

=

òò

òò

r

energia w przekroju

dx

I

G

M

L

L

S

e

ò

=

)

(

0

2

2

Wytrzymałość Materiałów, r.II, sem.III, wykład 6.

Jan Bielski

7

13

• stan czystego ścinania; ścięcie techniczne - obliczenia wytrzymałościowe

• założenia geometryczne (hipoteza Bernoulli’ego) dla skręcania prętów o przekrojach kołowo
symetrycznych

• analiza odkształceń skręcanego pręta

• naprężenia w stanie sprężystym

• warunek bezpieczeństwa

• obliczanie kątów skręcenia

• warunek sztywności

• energia odkształcenia sprężystego w skręcanym pręcie

Schemat obliczeń wytrzymałościowych

• -dane: geometria, obciążenia, dane materiałowe

• -wyznaczenie rozkładu momentu skręcającego

• -zlokalizowanie przekroju niebezpiecznego

• -spełnienie warunku bezpieczeństwa

® dobranie wymiarów, oszacowanie

dopuszczalnych obciążeń, sprawdzenie warunku bezpieczeństwa

• -wyznaczenie jednostkowego kąta skręcenia i kąta skręcenia wałka

• -spełnienie warunków sztywnościowych

® wymiary, obciążenia