MECHANIKA GRUNTÓW

MECHANIKA GRUNTÓW

Wykład 9

Równania opisuj ce stany napr e i odkształce w gruncie

(model liniowej spr ysto ci)

Opis stanów odkształce i napr e

ij

– współrz dne tensora napr enia

(6)

u - współrz dne wektora przemieszczenia (3)

u

i

- współrz dne wektora przemieszczenia (3)

ij

– współrz dne tensora odkształcenia

(6)

Ł cznie funkcji opisuj cych stany odkształce i napr e

(15)

Równania:

1) Równowagi wewn trzne (3)

i,j = 1,2,3

2) Geometryczne (6)

0

,

=

j

ji

σ

2) Geometryczne (6)

(

)

i

j

j

i

ij

u

u

,

,

2

1

+

=

ε

3) Fizyczne (konstytutywne) (6)

2

v

δ

σ

σ

ε

⋅

−

=

1

1

=

=

j

i

1

δ

Ł cznie równa opisuj cych stany napr e i odkształce : 15

ij

ii

ij

ij

G

v

G

δ

σ

σ

ε

⋅

+

−

=

2

1

2

≠

=

j

i

ij

0

δ

Równania opisuj ce stany napr e i odkształce w gruncie

(model liniowej spr ysto ci)

Po podstawieniu do równa fizycznych (3) równa geometrycznych (2 i dalej do (1)

otrzymujemy:

1

i=1,2,3

gdzie:

0

,

2

1

1

=

−

+

∆

i

i

v

G

u

G

ε

,

ε

ε

=

gdzie:

Otrzymane równania s układem równa ró niczkowych cz stkowych II-go rz du

typu eliptycznego

ii

,

ε

ε

=

typu eliptycznego

Warunki brzegowe (dla )

a) Przemieszczeniowe

B

x

∈

a) Przemieszczeniowe

b) Napr eniowe

B

i

B

x

i

u

u

=

∈

c) Mieszane

B

ij

x

ij

σ

σ

=

∈

B = Bu + B

B

ij

B

x

ij

B

i

Bu

x

i

u

u

σ

σ

σ

=

=

∈

∈

;

Równania opisuj ce stany napr e i odkształce w gruncie

(model liniowej spr ysto ci)

Dla zagadnienia dwuwymiarowego (płaskiego) mo na zapisa układ równa

dla napr e w postaci:

0

=

∂

∂

+

∂

∂

z

x

xz

xx

σ

σ

0

+

∂

∂

+

∂

∂

∂

∂

z

x

z

x

zz

xz

σ

σ

(

)

(

)

0

0

2

2

=

+

∂

+

+

∂

+

∂

+

∂

z

x

zz

xx

zz

xx

σ

σ

σ

σ

(

)

(

)

0

2

2

=

∂

+

∂

+

∂

+

∂

z

x

zz

xx

zz

xx

σ

σ

σ

σ

Do tego układu nale y doł czy odpowiednie warunki brzegowe.

Przy rozwi zywaniu zada płaskich jest zatem mo liwe:

1. Wyznaczy składowe stanu napr enia

1. Wyznaczy składowe stanu napr enia

2. Maj c pole napr e , wyliczy ze zwi zków fizycznych odkształcenia

3. Wyznaczy przemieszczenia, wykorzystuj c zwi zki geometryczne

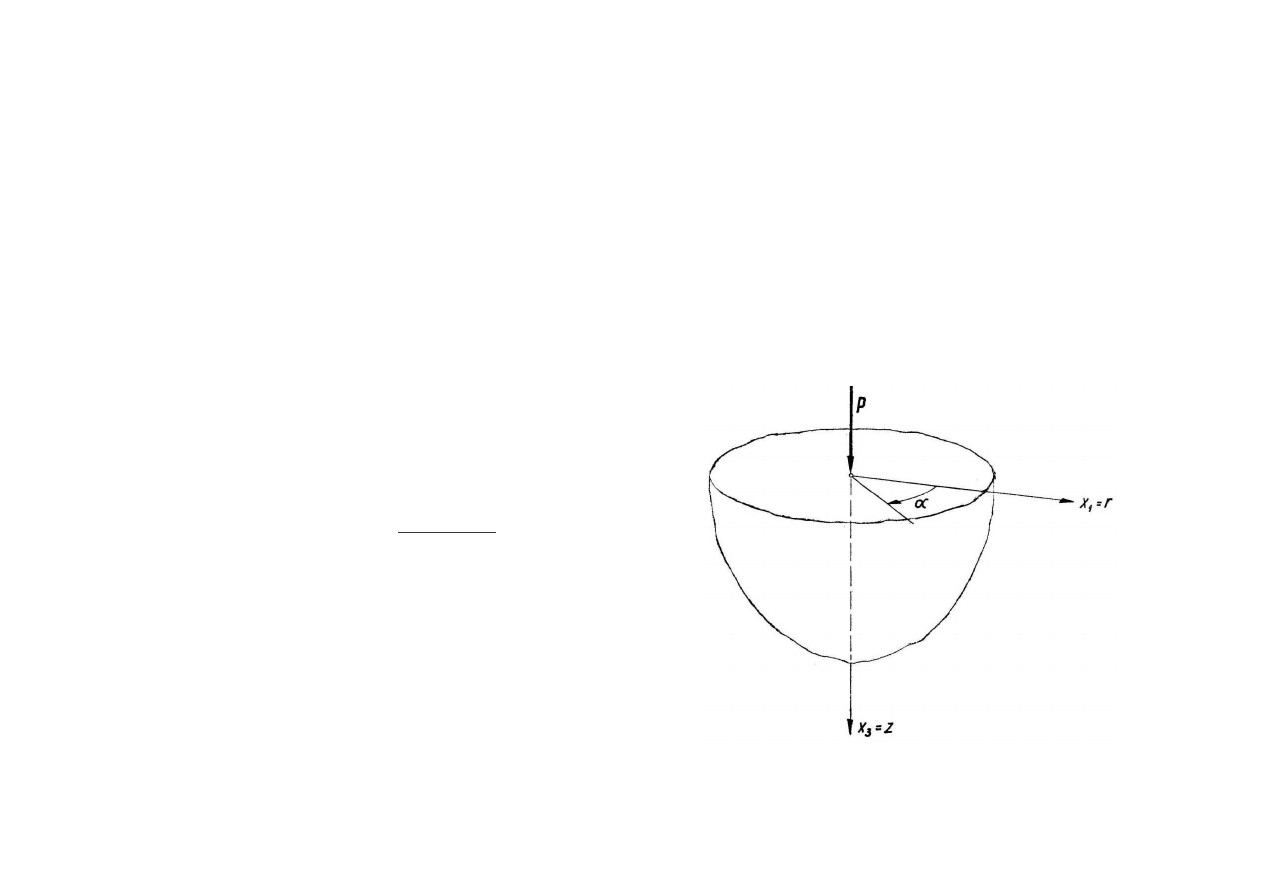
ZAGADNIENIE BOUSSINESQA

Brzeg półprzestrzeni jest obci ony normaln sił skupion .

Brak jest napr e stycznych.

Taki układ sił wywołuje osiowo-symetryczne stany: napr enia i odkształcenia.

Stosowny do opisu takiej sytuacji jest walcowy układ współrz dnych (r, ,z)

z funkcjami nie zale nymi od k ta .

z funkcjami nie zale nymi od k ta .

Warunki brzegowe przyjmuj posta :

)

(

−

=

z

r

r

P

δ

σ

0

=

−

=

z

r

P

σ

σ

0

=

rz

σ

ZAGADNIENIE BOUSSINESQA

Rozwi zanie zadania:

Przemieszczenia:

Rozwi zanie zadania:

(

) ( )

+

−

−

=

3

2

1

4

z

R

R

r

v

R

rz

v

P

u

Przemieszczenia:

u – przemieszczenie radialne

(

) ( )

(

)

+

−

=

+

3

2

3

1

2

4

4

R

z

R

v

v

P

w

z

R

R

R

v

w – przemieszczenie osiowe

+

=

3

4

R

R

v

w

Napr enia:

(

)

5

2

2

2

3

1

2

1

2

R

z

r

R

r

z

r

v

P

r

−

−

⋅

−

=

π

σ

Napr enia:

r

– napr enie radialne

5

3

2

3

R

z

P

z

−

=

π

σ

z

– napr enie osiowe

(

)

3

2

2

1

2

1

2

2

R

z

R

r

z

r

v

P

R

+

+

−

⋅

−

=

π

σ

π

α

– napr enie obwodowe

5

2

2

3

R

rz

P

rz

⋅

−

=

π

σ

rz

– napr enie styczne

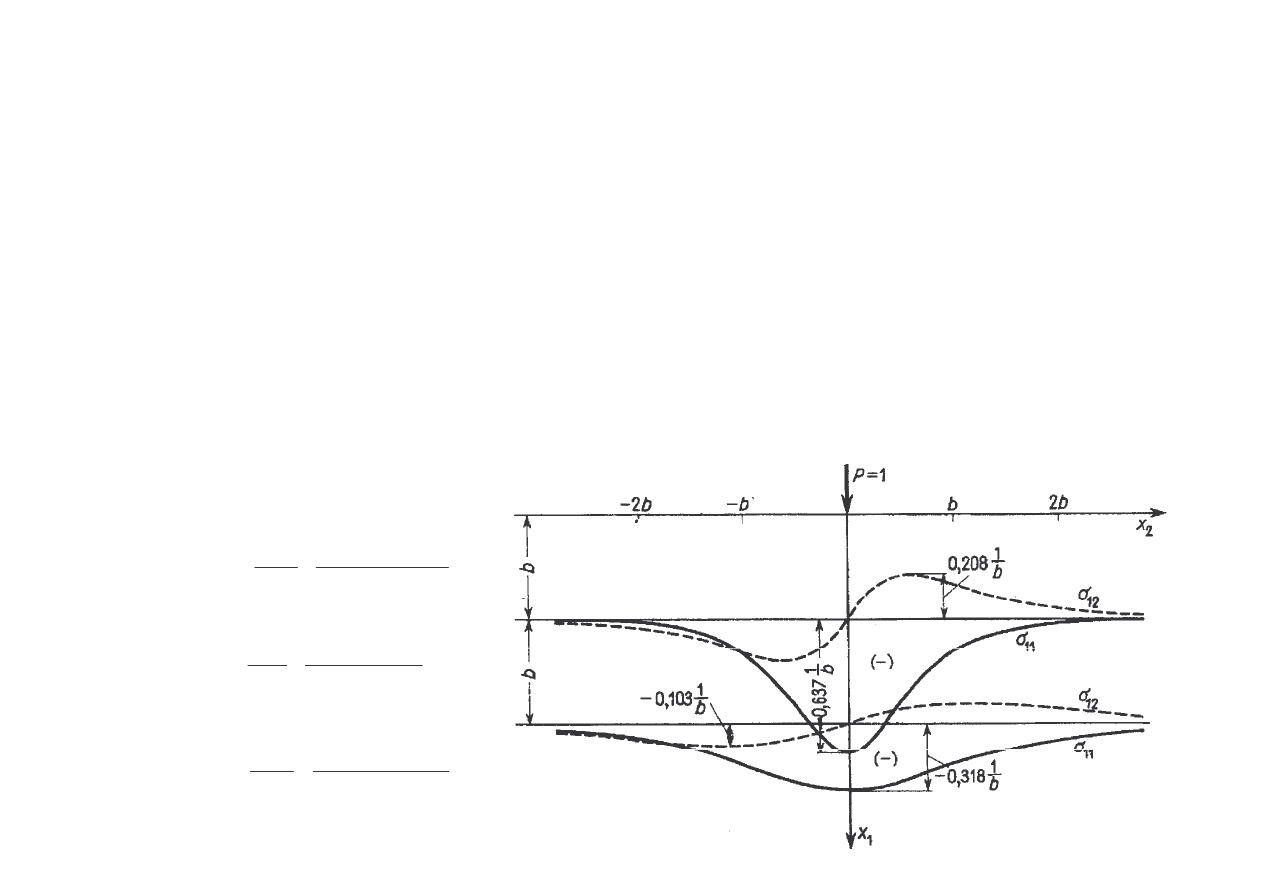
ZAGADNIENIE FLAMANTA

Na brzegu półprzestrzeni spr ystej działa liniowe obci enie P w kierunku osi x

3

.

Stany napr enia, odkształcenia wywołane takim obci eniem nazywaj si płaskimi

stanami napr enia, odkształcenia. Funkcje je opisuj ce w kartezja skim układzie

stanami napr enia, odkształcenia. Funkcje je opisuj ce w kartezja skim układzie

współrz dnych ale tylko od x

1

i x

2

.

Zagadnienie brzegowe w tym układzie współrz dnych opisuj równania:

Zagadnienie brzegowe w tym układzie współrz dnych opisuj równania:

0

)

(

2

11

=

⋅

−

=

σ

δ

σ

x

P

Rozwi zanie zagadnienia:

0

12

=

σ

3

2

x

P ⋅

−

=

σ

2

2

2

2

1

1

11

)

(

2

x

x

x

P

+

⋅

−

=

π

σ

2

2

x

x

P ⋅

−

=

σ

2

2

2

2

1

2

1

22

)

(

2

x

x

x

x

P

+

⋅

−

=

π

σ

2

2

x

x

P ⋅

−

=

σ

2

2

2

2

1

2

1

12

)

(

2

x

x

x

x

P

+

⋅

−

=

π

σ

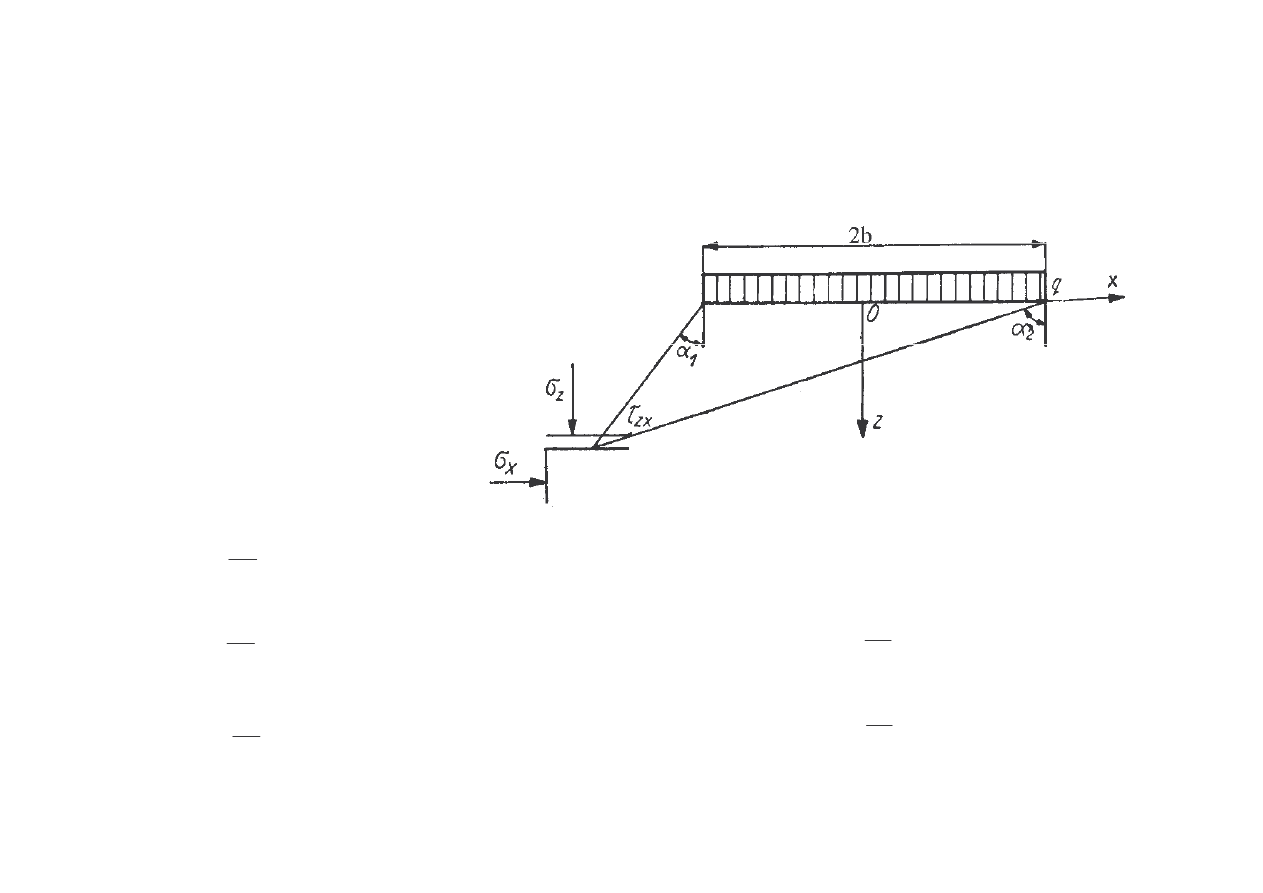
NAPR

ENIA W O RODKU GRUNTOWYM

OBCI

ENIE ROZŁO ONE RÓWNOMIERNIE

(ZADANIE PŁASKIE)

(ZADANIE PŁASKIE)

Warunek brzegowy:

0

=

−

=

z

q

σ

σ

Warunek brzegowy:

0

=

xz

σ

)

2

cos

2

sin

2

(

ω

ε

ε

σ

⋅

+

⋅

=

q

Rozwi zanie:

)

2

cos

2

sin

2

(

ω

ε

ε

π

σ

⋅

+

⋅

=

q

z

)

2

cos

2

sin

2

(

ω

ε

ε

π

σ

⋅

−

⋅

=

q

)

2

sin

2

(

1

ε

ε

π

σ

+

⋅

=

q

Napr enia główne:

)

2

cos

2

sin

2

(

ω

ε

ε

π

σ

⋅

−

⋅

=

x

ω

ε

π

σ

2

sin

2

sin

⋅

⋅

=

q

xz

)

2

sin

2

(

1

ε

ε

π

σ

+

⋅

=

)

2

sin

2

(

3

ε

ε

π

σ

−

⋅

= q

ω

ε

π

σ

2

sin

2

sin

⋅

⋅

=

xz

π

1

2

2

1

2

2

α

α

ε

α

α

ω

−

=

+

=

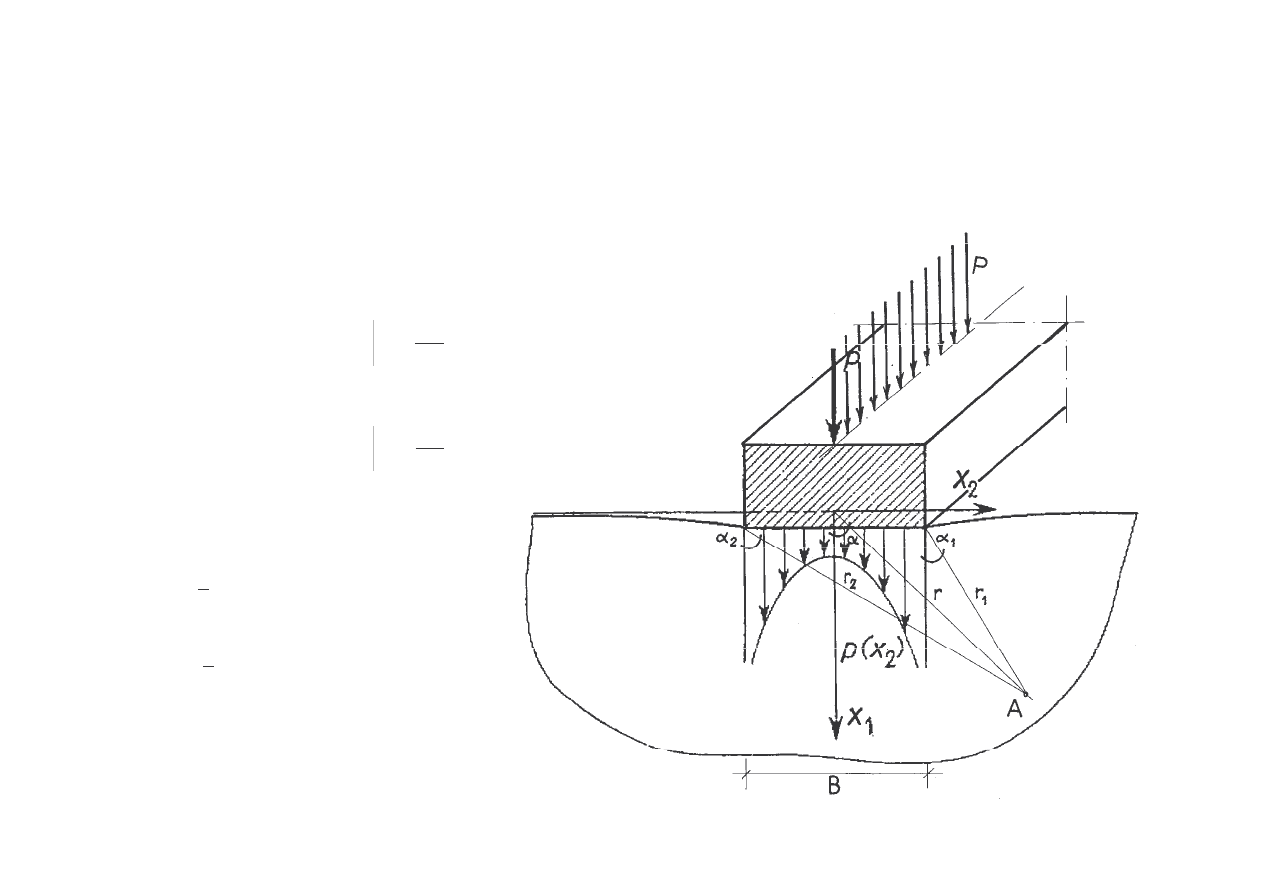
NAPR

ENIA W O RODKU GRUNTOWYM

OBCI

ENIE SZTYWNYM FUNDAMENTEM

OBCI

ENIE SZTYWNYM FUNDAMENTEM

(ZADANIE PŁASKIE)

Sformułowanie zadania:

<

=

B

x

w

w

0

2

2

>

=

<

=

B

x

x

w

w

B

σ

0

0

2

0

2

2

2

1

2

>

=

>

=

x

x

x

x

x

σ

σ

0

0

2

2

1

>

=

x

x

x

σ

−

=

2

2

2

)

(

B

B

P

dx

x

p

−

2

2

2

B

NAPR

ENIA W O RODKU GRUNTOWYM

OBCI

ENIE SZTYWNYM FUNDAMENTEM

OBCI

ENIE SZTYWNYM FUNDAMENTEM

(ZADANIE PŁASKIE)

Rozwi zanie zadania:

Rozwi zanie zadania:

−

+

−

=

)

3

cos(

cos

cos

2

1

2

2

1

1

ω

α

α

ω

π

σ

r

r

r

r

r

P

2

1

2

1

π

r

r

r

r

−

−

−

=

)

3

cos(

cos

cos

2

1

2

2

1

2

ω

α

α

ω

π

σ

r

r

r

r

r

P

2

1

2

1

)

3

sin(

cos

2

1

2

2

1

12

ω

α

α

π

σ

−

=

r

r

r

r

r

P

+

−

=

α

ω

σ

cos

cos

2

r

P

Napr enia główne:

Napr enia kontaktowe:

+

−

=

α

ω

π

σ

cos

cos

2

1

2

1

1

r

r

r

r

r

P

−

−

=

α

ω

σ

cos

cos

2

r

P

2

2

2

)

(

x

B

P

x

p

−

−

=

π

−

−

=

α

ω

π

σ

cos

cos

2

1

2

1

2

r

r

r

r

r

P

2

2

2

x

B −

π