COSMOSFFE Thermal
1-1
1
Introduction
Introduction
COSMOSFFE Thermal is a fast, robust, and accurate finite element program for the
analysis of linear static structural problems. The program exploits a new technology
developed at Structural Research for the solution of large systems of simultaneous
equations using sparse matrix technology along with iterative methods combined
with novel database management techniques to substantially reduce solution time,
disk space, and memory requirements.
COSMOSFFE Thermal has been written from scratch using state of the art
techniques in FEA with two goals in mind: 1) to address basic design needs, and 2)
to use the most efficient possible solution algorithms without sacrificing accuracy.
The program is particularly suitable for the solution of large models subjected to a
variety of loading and boundary conditions environments.
The program can analyze linear and nonlinear steady state and transient heat
conduction problems with convective and radiative type boundary conditions in
one, two, and three dimensional geometries.
In
de
x
In
de
x

Chapter 1 Introduction
1-2
COSMOSFFE Thermal
Theoretical Backround
The governing equation for conduction heat transfer is:
ρC ∂T / ∂t = ∂/∂x(k
x
∂T/∂x) + ∂/∂y(k
y
∂T/∂y) + ∂/∂z(k
z
∂T/∂z) + Q
(1-1)
where:
T
= Temperature
t
= Time
ρ
= Density
C
= Specific heat
k
x
, k
y
, k
z
= Thermal conductivities in global X, Y and Z directions respectively
Q
= Volumetric heat generation rate
Boundary Conditions
The following boundary conditions and loads can be modeled with FFE Thermal.
Specified Temperature
Temperature can be prescribed on any part of the model boundary.
T
s
= T
o
(1-2)
T
s
= Surface temperature
T
o
= Specified temperature
Convection
Convection can be applied to any part of the model boundary.
Heat flux = q = h
c
(T
s
- T
∞
)
(1-3)
h
c
= Convection coefficient
T
s
= Surface temperature
T
∞
= Ambient temperature
In
de
x
In
de
x

COSMOSFFE Thermal
1-3
Chapter 1 Introduction
Radiation
Radiation can be applied to any part of the model boundary.
Heat flux = q =
σε(T
s
4
- T
∞
4
)
(1-4)
σ = Stefan - Boltzmann constant
ε =
Emissivity
T
s
= Surface temperature
T
∞
= Ambient temperature
Applied Heat Flux
Heat flux can be applied to any part of the model boundary.
q = Applied heat flux = - K(
∂T/∂n)
s
(1-5)
K
= Thermal conductivity
(
∂T/∂n)
s
= Normal temperature gradient on the surface
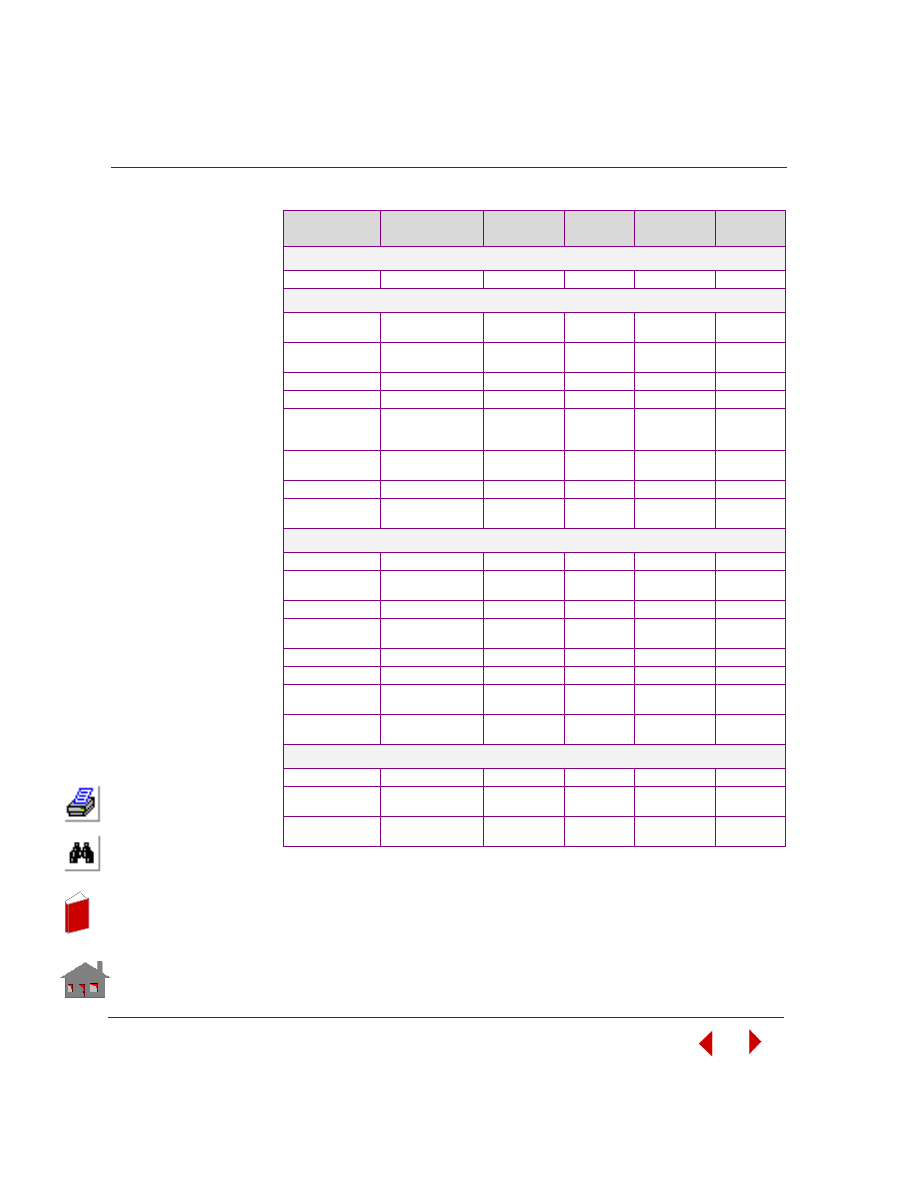
Consistent Systems of Units
In COSMOSM modules including FFE Thermal, you are free to adopt standard or
non-standard systems of units, but you are responsible for consistency and the
interpretation of the units of results. The table below shows consistent standard
systems of units for the physical quantities used in the FFE Thermal module.
In
de
x
In
de
x
Chapter 1 Introduction
1-4
COSMOSFFE Thermal
Table B-8. Table of Consistent Units for Heat Transfer Analysis
Description
COSMOS Name
* FPS
1
(gravitational)
* SI
2
(absolute)
* MKS
3
(gravitational)
CGS
4
(absolute)
Measure
Length
X, Y, Z
in
m
cm
cm
Material Properties
Thermal
Conductivity
KX, KY, KZ
BTU/in sec
∞
F
W/m
∞
K
Cal/cm sec
∞
C
W/cm
∞
K
Specific Heat
C
BTU in/lbs
sec
2
°
F
J/kg
°
K
Cal cm/kg
sec
2
°
C
J/g
°
K
Mass Density
DENS
lbs sec
2
/in
4
kg/m
3
kg
sec
2
/cm
4
g/cm
3
Emissivity
EMIS
no units
no units
no units
no units
Stefan Boltzmann
Constant
SB_CONST
3.3063e-15
BTU/sec in
2
°
R
4
5.6703e-8 W/
m
2
°
K
4
1.3552e-12 Cal/
sec cm
2
°
K
4
5.6703e-12
W/cm
2
°
K
4
Convection Film
Coefficient
HC (for CLINK
elements)
BTU/sec in
2
°
F
W/m
2
°
K
Cal/sec cm
2
°
C
W/cm
2
°
K
Material Angle
Beta
degree
degree
degree
degree
Electric
Conductivity
ECONX
mho/in
mho/m
mho/m
10
-13
mho/
cm
Loads and Boundary Conditions
Temperature
Temp, TREF, NT
°
F
°
K
°
C
°
K
Absolute
Temperature Offset
TOFFSET
460
°
R
none
273
°
K
none
Time
Time
seconds
seconds
seconds
seconds
Concentrated
Heating
Nodal Heat, Q
BTU/sec
Watt
Cal/sec
Watt
Volume Heating
Element Heat, QE
BTU/sec in
3
W/m
3
Cal/sec cm
3
W/cm
3
Surface Heating
Heat Flux, HX
BTU/sec in
2
W/m
2
Cal/sec cm
2
W/cm
2
Convection Film
Coefficient
CE
BTU/sec in
2
°
F
W/m2
°
K
Cal/sec cm
2
°
C
W/cm
2
°
K
Radiation
Emissivity
RE
no units
no units
no units
no units
Results
Temperature
Temp
°
F
°
K
°
C
°
K
Temperature
Gradient
GRADX, GRADY,
GRADZ
°
F/in
°
K/m
°
C/cm
°
K/cm
Heat Flux
HFLUXX, HFLUXY,
HFLUXZ, HFLUXN
BTU/sec in
2
W/m
2
Cal/sec cm
2
W/cm
2
In
de
x
In
de
x

COSMOSFFE Thermal
2-1
2
Capabilities
Introduction
The following are some important features of COSMOSFFE Thermal.
Analysis Features
•
Linear and nonlinear, steady-state and transient heat transfer
•
Temperature-dependent material properties
•
Time- and temperature-dependent heat sources and sinks
•
Time- and temperature-dependent or heat flux, convection and radiation
boundary conditions:
-
Heat Flux
-
Convection
-
Radiation
•
Time-dependent prescribed temperatures
•
First and second order elements
•
Heat Transfer - Structural coupling where resulting temperatures can be
included in structural problems
•
Restart option for transient problems
In
de
x
In
de
x

Chapter 2 Capabilities
2-2
COSMOSFFE Thermal
Internal Heat Generation
Internal heat generation can be applied to any node or element of the model.
Material properties
FFE Thermal supports isotropic materials. Orthotropic material properties, if
defined, are always considered in the global coordinate system only.
Temperature- and Time-Dependent Properties
Temperature curves are used to specify the variation of material properties with
temperature and they are also used to prescribe the variation of convection
coefficient, heat generation rate, surface emissivity, and heat fluxes with
temperature. Time curves are used to specify the variation of parameters such as
convection, temperature, etc. with time.
Temperature-dependent convection coefficients are calculated based on the average
film temperatures (T
s
+ T
∞
)/2. Temperature dependent emissivities or heat fluxes
are calculated based on the surface temperature.
Thermal Stress Analysis
Once a thermal analysis is completed, resulting temperature distribution can be
used to calculate thermal stresses in the material, using the FFEStatic or STAR.
Size Limits
Three variation of GEOSTAR are installed on your computer, the three variations
support 64,000, 128,000,and 256,000 nodes and elements, respectively. Each
variation may be started by double-clicking the corresponding icon in the
COSMOSM 2.0 program group The limits represent the maximum node and
In
de
x
In
de
x

COSMOSFFE Thermal
2-3
Chapter 2 Capabilities
element labels that may be created in GEOSTAR. Please note that these variations
are not compatible with each other. The session and neutral (gfm) files are however
compatible.
The following table shows size limitations for some entities related to thermal
analysis. Refer to the COSMOSM User's Guide for more information about the size
limitations.
Table 2-1. Size Limitations for Thermal Analysis in COSMOSM
Entity
Limits
Time curves
Points for a time curve definition
100
5000
Temperature curves
Points for a temperature curve definition
100
5000
Time steps
6000
In
de
x
In
de
x

2-4
COSMOSFFE Thermal
In
de
x
In
de
x
COSMOSFFE Thermal
3-1
3
Element Library
Introduction
The COSMOSFFE Thermal module features an extensive element library to satisfy
your finite element modeling and analysis requirements for all types of practical
heat transfer problems. These elements model the behavior of 1D, 2D, and 3D
problems in linear and nonlinear steady-state and transient heat transfer
computations. The following table lists the elements available for analysis in the
COSMOSFFE Thermal module.
Table 3-1. Elements for Thermal Analysis
Type
Name
Order
Two dimensional elastic beam element
BEAM2D
First
Three dimensional elastic beam element
BEAM3D
First
Convection link
CLINK
. . .
4/8-node plane and axisymmetric element
PLANE2D
First/Second
Radiation link
RLINK
. . .
3-node thin shell element
SHELL3
First
3-node thick shell element
SHELL3T
First
4-node thin shell element
SHELL4
First
4-node thick shell element
SHELL4T
First
8/20-node 3D solid element
SOLID
First/Second
In
de
x
In
de
x
Chapter 3 Element Library
3-2
COSMOSFFE Thermal
Table 3-1. Elements for Thermal Analysis (Concluded)
The elements in the above table are defined using the
EGROUP
(Propsets >
Element Group
) command shown in the table below. Table 3-2 lists other
commands for the manipulation of the associated element attributes. These
commands can be reached from the Control Panel by following the menu path
given between parenthesis.
Table 3-2. Commands for Element Group Definition, Modification, and Listing
Type
Name
Order
4-node tetrahedral solid element
TETRA4
First
10-node tetrahedral solid element
TETRA10
Second
3/6-node triangular plane and axisymmetric element TRIANG
First/Second
Two dimensional truss/spar element
TRUSS2D
First
Three dimensional truss/spar element
TRUSS3D
First
Command
Function
Comments
EGROUP (Propsets >
Element Group
)
Defines element groups
and the associated
element analysis options.
The maximum number of
element groups permitted in
a model is 20.
EPROPSET (Propsets
>
New Property Set
)
Assigns the existing
element group, material
property, and real constant
groups as well as element
coordinate system to newly
created elements.
EPROPCHANGE
(Propsets >
Change
El-Prop
)
Changes the association
between element groups,
real constants sets, and
material property sets.
EGLIST (Edit > LIST >
Element Groups
)
Lists specified element
groups and the associated
element analysis options.
The on-screen listing can be
piped to a text file if desired,
using the LISTLOG (Control >
MISCELLANEOUS >
List Log
)
command.
In
de
x
In
de
x

COSMOSFFE Thermal
3-3
Chapter 3 Element Library
The elements described in Table 3-1 can be classified based on the dimensionality
of the problem. TRUSS2D, TRUSS3D, BEAM2D and BEAM3D elements are
line elements to be used for 1D heat transfer analysis. PLANE2D, TRIANG,
SHELL3, SHELL4, SHELL3T, and SHELL4T are area elements to be used for
2D problems. SOLID, TETRA4, and TETRA10 are volume elements to be used for
3D heat transfer analysis. CLINK and RLINK elements are line elements but
applicable for all types of thermal problems, whether 1D, 2D, or 3D.
Every element in Table 3-1 has different analysis and modeling options (maximum
of eight entries), designated as OP1, …, OP8. When you execute the
EGROUP
command, you are prompted for their input with sufficient physical interpretation
for the selected element.
✍
The order of the elements to be used in the analysis is controlled
by the
A_FFETHERMAL
(Analysis > HEAT TRANSFER >
FFE
Thermal Options
) command, not by the number of nodes generated in
preprocessing for TRIANG, PLANE2D, SOLID, TETRA4, and
TETRA10 elements. Four options are possible: 1) Use second order
elements in analysis with second order elements in preprocessing. 2)
Use second order elements in analysis with first order elements in
preprocessing. 3) Use first order elements in analysis with first order
elements in preprocessing. 4) Use first order elements in analysis
with second order elements in preprocessing.
The following figure shows pictorial representations of all elements available in the
COSMOSFFE Thermal module. COSMOSM User Guide (Volume 1) presents a
detailed description of all elements in Chapter 4, Element Library.
In
de
x
In
de
x

Chapter 3 Element Library
3-4
COSMOSFFE Thermal
Figure
3-1.
Elements for Linear and Nonlinear Steady-State
and Transient Heat Transfer Analyses
4 - Node P la ne or
Ax is y mme t ric
Q ua drila t e ra l
Element: PLANE2D
Nodes: 4
8 - Node P la ne or
Ax is y mme t ric
Q ua drila t e ra l
Element: PLANE2D
Nodes: 8
3 - Node P la ne or
Ax is y mme t ric
Tria ngle
Element: TRIANG
Nodes: 3
6 - Node P la ne or
Ax is y mme t ric
Tria ngle
Element: TRIANG
Nodes: 6
3 - Node S he ll
Element: SHELL3 or
SHELL3T
Nodes: 3
4 - Node S he ll
Element: SHELL4 or
SHELL4T
Nodes: 4
4 - Node
Te t ra he dra l S olid
Element: TETRA4
Nodes: 4
1 0 - Node
Te t ra he dra l S olid
Element: TETRA10
Nodes: 10
8 - Node S olid
Element: SOLID
Nodes: 8
2 0 - Node S olid
Element: SOLID
Nodes: 20
Firs t O rde r
P ris m- S ha pe d S olid
Element: SOLID
Nodes: 8 with a face
collasping to
an edge
S e c ond O rde r
P ris m- S ha pe d S olid
Element: SOLID
Nodes: 20 with a face
collasping to
an edge
Trus s / S pa r
Element: TRUSS2D or
TRUSS3D
Nodes: 2
Be a m
Element: BEAM2D or
BEAM3D
Nodes: 2 or 3
Conv e c t ion Link
Element: CLINK
Nodes: 2 or 3
Ra dia t ion Link
Element: RLINK
Nodes: 2 or 3
In
de
x
In
de
x
COSMOSFFE Thermal
4-1
4
Input Data
Introduction
Proper modeling and analysis specifications are crucial to the success of any finite
element analysis. Irrespective of the type of analysis, numerical solution using
finite element analysis requires complete information on the model under
consideration. The finite element model you submit for analysis must contain all
the necessary data for each step of numerical simulation - geometry, elements,
loads, boundary conditions, solution of system of equations, visualization and
output of results, etc. This chapter attempts to conceptually illustrate the procedure
for building a model for analysis using the COSMOSFFE Thermal module.
Since a major portion of the effort in building a finite element model is made in
geometry creation and meshing, these topics will not be discussed here. The
COSMOSM User Guide (Volume 1) presents in-depth information on the
procedures for model building and postprocessing in GEOSTAR. This chapter
therefore only outlines those commands which are relevant for analysis in the
COSMOSFFE Thermal module.
✍
For a detailed description of all commands, refer to the COSMOSM
Command Reference Manual (Volume 2).
In
de
x
In
de
x
Chapter 4 Input Data
4-2
COSMOSFFE Thermal
Modeling and Analysis Cycle in the
COSMOSFFE Thermal Module
The basic steps involved in a finite element analysis are:
•
Create the problem geometry.
•
Mesh the defined geometry with appropriate type of element(s).
•
Apply constraints on the finite element model.
•
Define the loads on the model.
•
Define the material and sectional properties.
•
Submit the completed finite element model for analysis.
•
Interpret and analyze the results.
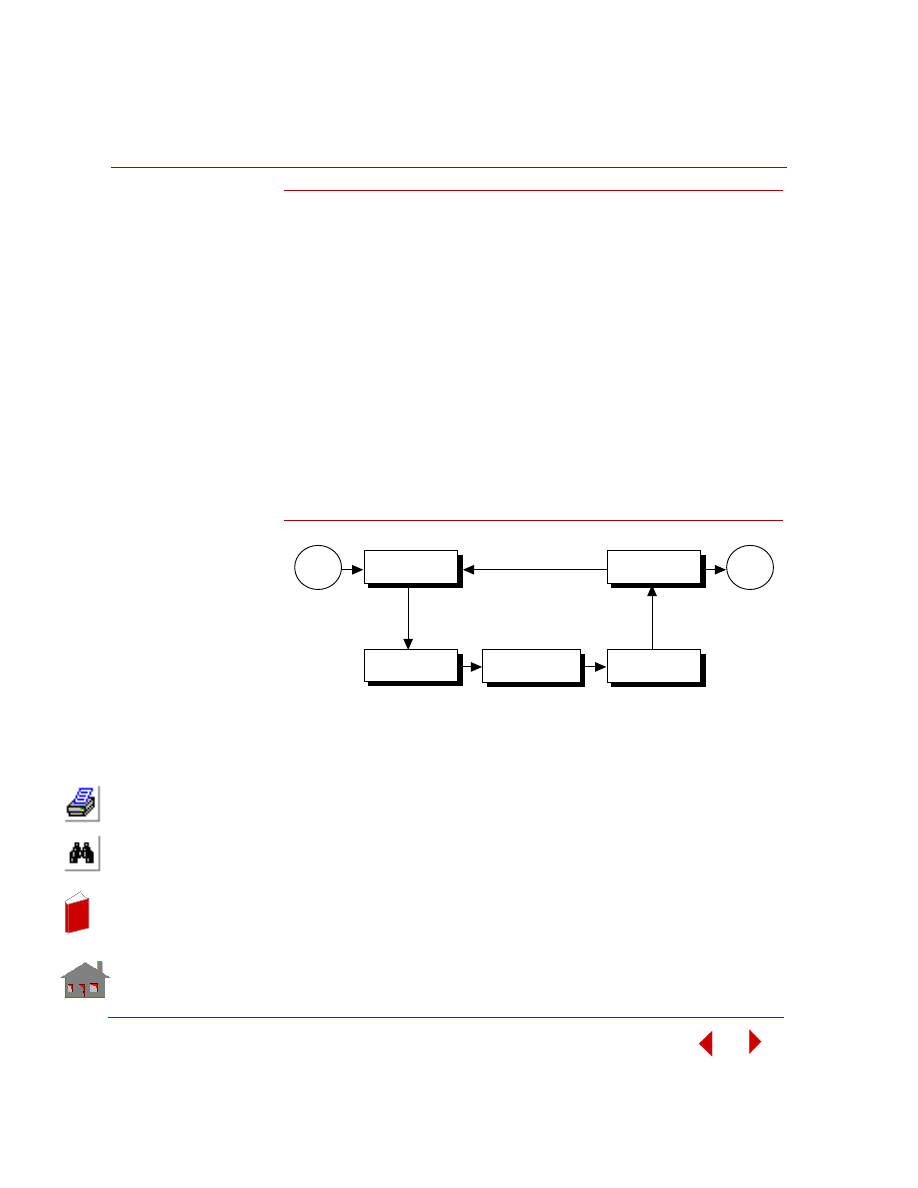
These steps can be schematically represented as shown in the figure below.
Figure 4-1. Finite Element Modeling and Analysis Steps
Preprocessing refers to the operations you perform such as defining the model
geometry, mesh generation, applying loads and boundary conditions, and other
operations that are required prior to submitting the model for analysis. The term
analysis in the above figure refers to the phase of specifying the analysis options
and executing the actual analysis. Postprocessing refers to the manipulation of the
analysis results for easy understanding and interpretation in a graphical
environment.
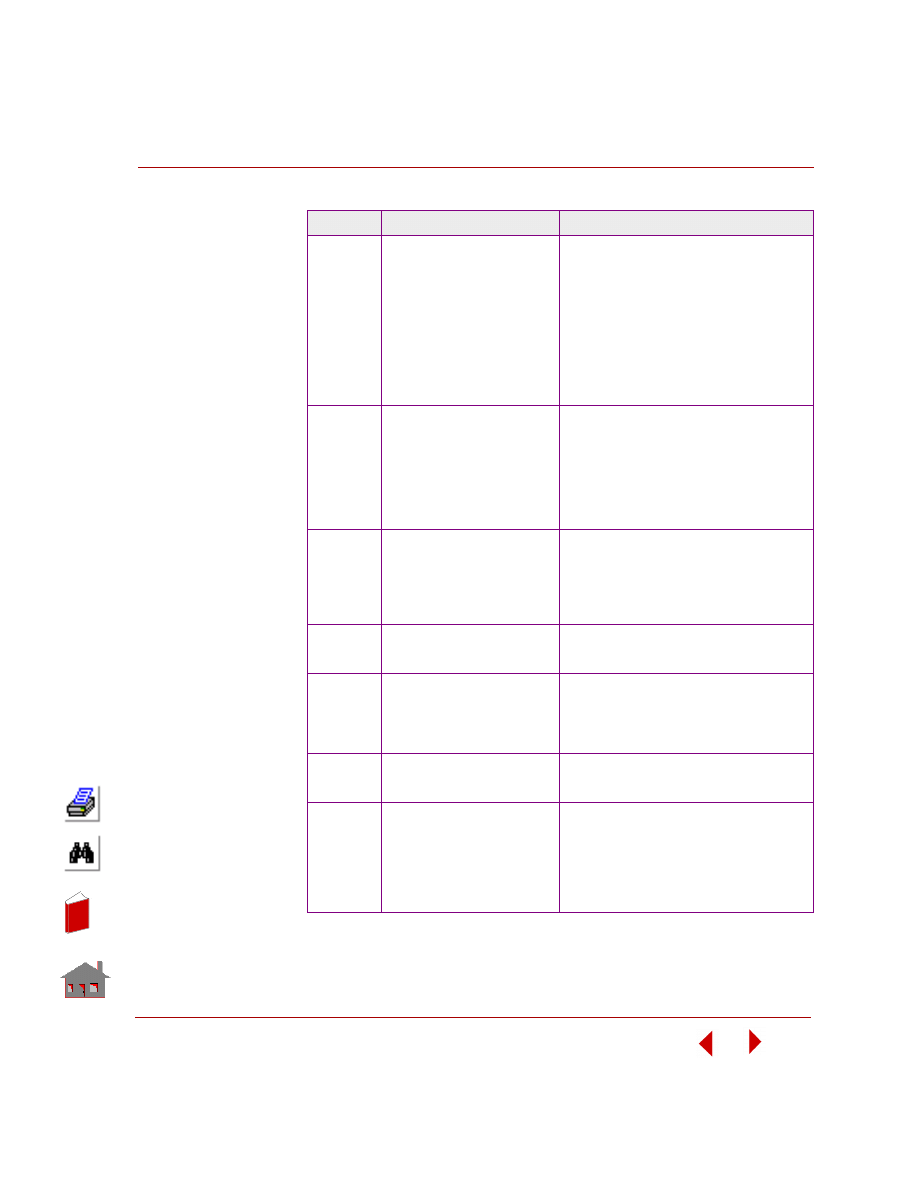
The commands summarized in the table below provide you with information on the
input of element groups, material and sectional properties, loads and boundary
conditions, analysis specifications, and output specifications.
START
PREPROCESSING
POSTPROCESSING
STOP
Analysis and
Design Decisions
Problem Definition
ANALYSIS
In
de
x
In
de
x
COSMOSFFE Thermal
4-3
Chapter 4 Input Data
Table 4-1. Commands for Thermal Analysis
Function
Using COSMOSM Menu
Typing the Command
Property
Definition
Propsets
> Element Group
> Material Property
> Real Constant
> Pick Material Lib
> User Material Lib
> Material Browser
> AISC Sect Table
> Change El-Prop
> New Property Set
> Beam Section
. . .
EGROUP
MPROP
RCONST
PICK_MAT
USER_MAT
R_MATLIB
PICK_SEC
EPROPCHANGE
EPROPSET
BMSECDEF
Loads and
Boundary
Conditions
LoadsBC
> THERMAL
> TEMPERATURE
> NODAL HEAT
> ELEMENT HEAT
> HEAT FLUX
> CONVECTION
> RADIATION
. . .
. . .
NT_ commands for nodal temperatures *
Q_ commands for nodal heat generation *
QE_ commands for element heat generation *
HX_ commands for heat flux *
CE_ commands for convection *
RE_ commands for radiation *
Model
Verification
Meshing
> ELEMENTS
> Check Element
Analysis
> Data Check
> Run Check
. . .
. . .
E_CHECK
. . .
DATA_CHECK
R_CHECK
Specifying
Analysis
Options
Analysis
> HEAT TRANSFER
> FFE Thermal Options
. . .
. . .
A_FFETHERMAL
Specifying
Output
Options
Analysis
> HEAT TRANSFER
> Thermal Output Options
> OUTPUT OPTIONS
> Set Print Options
. . .
. . .
HT_OUTPUT
. . .
PRINT_OPS
Executing
Thermal
Analysis
Analysis
> HEAT TRANSFER
> Run Thermal Analysis
. . .
. . .
R_THERMAL
Postpro-
cessing
Results
> PLOT
> Thermal
> LIST
> Thermal Result
> EXTREMES
> Min/Max Temperature
. . .
ACTTEMP
TEMPPLOT
. . .
TEMPLIST
. . .
TEMPMAX
*See Command Reference Manual for complete definitions of the command.
In
de
x
In
de
x

Chapter 4 Input Data
4-4
COSMOSFFE Thermal
Temperature and Time Curves
Temperature and time curves are used to specify the variation of temperature and
time dependent properties, respectively. Using a time or temperature curve involves
the following steps.
•
Define the temperature or time curve using the
CURDEF
(LoadsBC >
FUNCTION CURVE >
Time/Temp Curve
) command. The created curve is
automatically activated.
•
Define the entity of interest (boundary condition, load, material property etc.).
•
Deactivate the curve using
ACTSET
(Control > ACTIVATE >
Set Entity
)
command so that this curve is not inadvertently associated with some other
entity defined later on.
For example, prescription of a temperature varying thermal conductivity may be
done as follows. Issue the
CURDEF
(LoadsBC > FUNCTION CURVE >
Time/
Temp Curve
) command to define temperature curve number 1 and then issue the
following sequence of commands:
Geo Panel:
Control > ACTIVATE >
Set Entity
Set Label >
Temperature Curve
Click on Continue icon
Load case set number >
1
Accept entries
Geo Panel:
Propsets >
Material Property
Material Property Set [1] >
Material Property Name >
X
Thermal Conductivity Property value [0.0] >
1.0
Accept all entries
Geo Panel:
Control > ACTIVATE >
Set Entity
Set Label >
Temperature Curve
Click on Continue icon
Load case set number >
0
Accept entries
In
de
x
In
de
x

COSMOSFFE Thermal
4-5
Chapter 4 Input Data
Thermal Stress Analysis
Once a thermal analysis is completed, resulting temperature profiles can be used to
calculate corresponding thermal stresses. The following steps can be used to
calculate thermal stresses:
•
Complete the thermal analysis.
•
Use
TEMPREAD
(LoadsBC > LOAD OPTIONS >
Read Temp as Load
)
command to assign the heat transfer results at a specific time step to a specific
load case for stress computation. Repeat the
TEMPREAD
command to assign
time steps to different load cases if desired.
•
Activate thermal loading using the
A_FFESTATIC
(Analysis > STATIC >
FFE
Static Options
) command.
•
Run the static analysis using
R_STATIC
(Analysis > STATIC >
Run Static
Analysis
) command.
Thermal Analysis Options
The A_FFETHERMAL Command
Geo Panel:
Analysis > HEAT TRANSFER >
FFE Thermal Options
The
A_FFETHERMAL
(Analysis > HEAT TRANSFER >
FFE Thermal Options
)
command specifies analysis options for heat transfer analysis using the FFE
Thermal module. Note that the
A_THERMAL
(Analysis > HEAT TRANSFER >
Thermal Analysis Options
) command specifies analysis options for heat transfer
analysis using the HSTAR module.
Entry & Option Description
analysis-option
Type of analysis to be performed.
S
Steady-state
T
Transient
(default is S)
element-order
Order of the element to be used. In spite of the element group name in the data-
base, you may specify through this option whether first (linear) or second (para-
bolic) elements will be used. As an example, if you define TETRA4 elements
and use second order, middle nodes on straight edges will be considered during
In
de
x
In
de
x

Chapter 4 Input Data
4-6
COSMOSFFE Thermal
analysis. On the other hand you may define TETRA10 elements and specify to
use first order. SOLID elements are treated similarly except that for these ele-
ments the same element group names are used for both first and second orders.
1
Use first order elements
2
Use second order elements
(default is 2)
tolerance
Convergence tolerance for nonlinear problems.
(default is 0.001)
unused-option
Unused option preserved for backward compatibility only.
mass-form
Mass matrix formulation used for transient analysis. It also affects matrix-for-
mulation for convection and radiation.
1
Lumped (ignored if selected with second order elements)
2
Consistent
(default is 1)
Running Thermal Analysis
The
R_THERMAL
(Analysis > HEAT TRANSFER >
Run Thermal Analysis
)
command performs thermal analysis using HSTAR or FFE Thermal. The command
runs the conventional HSTAR or the FFE Thermal module depending on the option
specified by the
A_FFETHERMAL
or the
A_THERMAL
commands. The command
will run the HSTAR module if none of the commands have been issued.
Postprocessing
The output generated by the thermal analysis can be viewed graphically in
GEOSTAR. From the Geo Panel, select Results > PLOT >
Thermal
in order to have
a contour plot of temperature, gradient or heat flux. An option menu will appear on
the screen to specify the plotting options. Note that if the user preferred to type the
command using the keyboard, two commands would have been used, namely,
ACTTEMP
and
TEMPLOT
commands. You may also look at the time history of
temperature, gradient, etc. at any node. First issue the
ACTXYPLOT
(Display > XY
PLOTS >
Activate Post-Proc
) to load the proper data into memory and then issue
XYPLOT
(Display > XY PLOTS >
Plot Curves
) to plot the time history of the
selected item.
In
de
x
In
de
x
COSMOSFFE Thermal
4-7
Chapter 4 Input Data
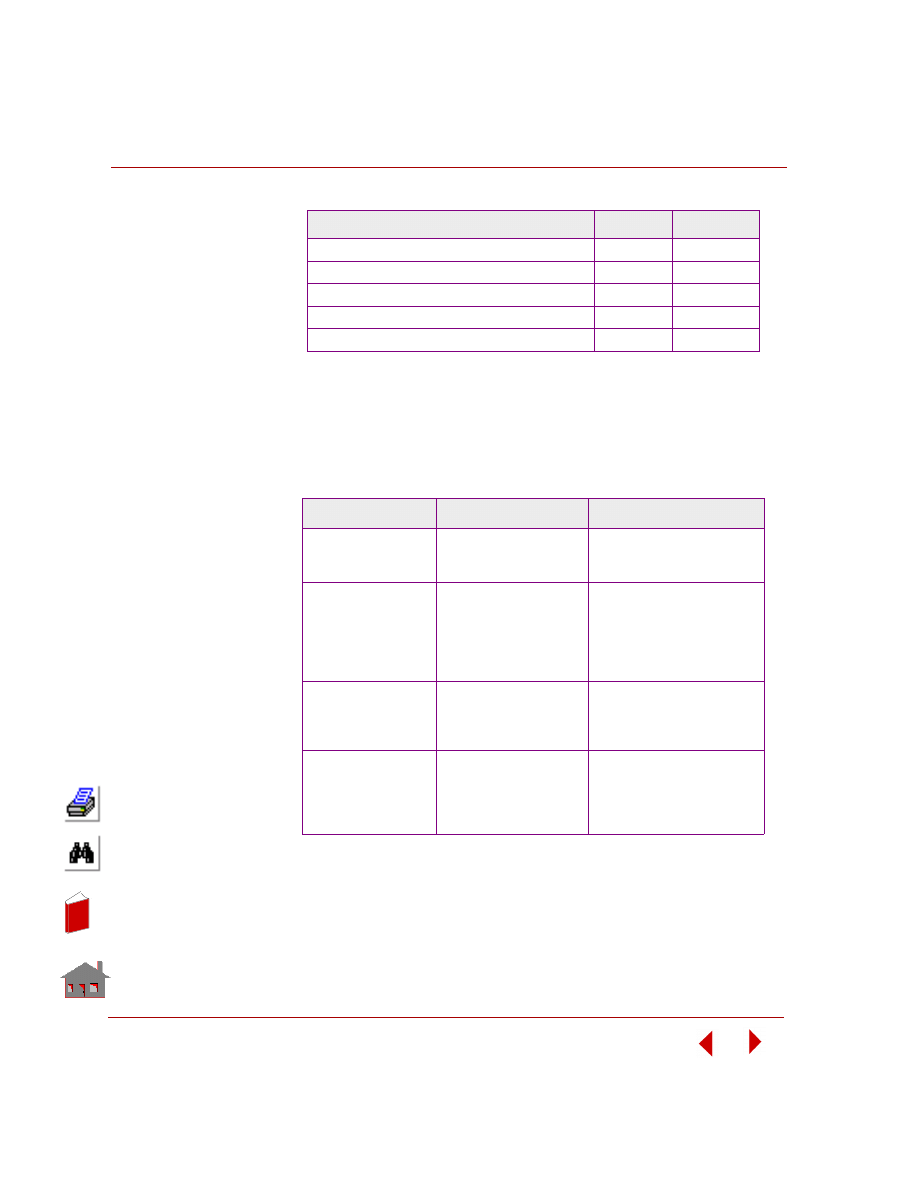
Verification of Model Input Data
One of the difficulties you may come across in the solution of small or large
problems alike is avoiding errors in the model input data. Some of the errors can be
detected by plotting the model in various positions, listing the element
connectivities, listing material and sectional properties, plotting or listing loads and
constraints, and many other on-line tools. For small problems, it is often easier to
perform these checks to see if all required input data have been properly generated
and defined. However, you may still miss some errors that are not easily
identifiable. For these types of situations and also for larger problems, it is plausible
to perform model checks in an automated environment. COSMOSFFE provides
powerful tools to automatically verify the robustness and validity of the finite
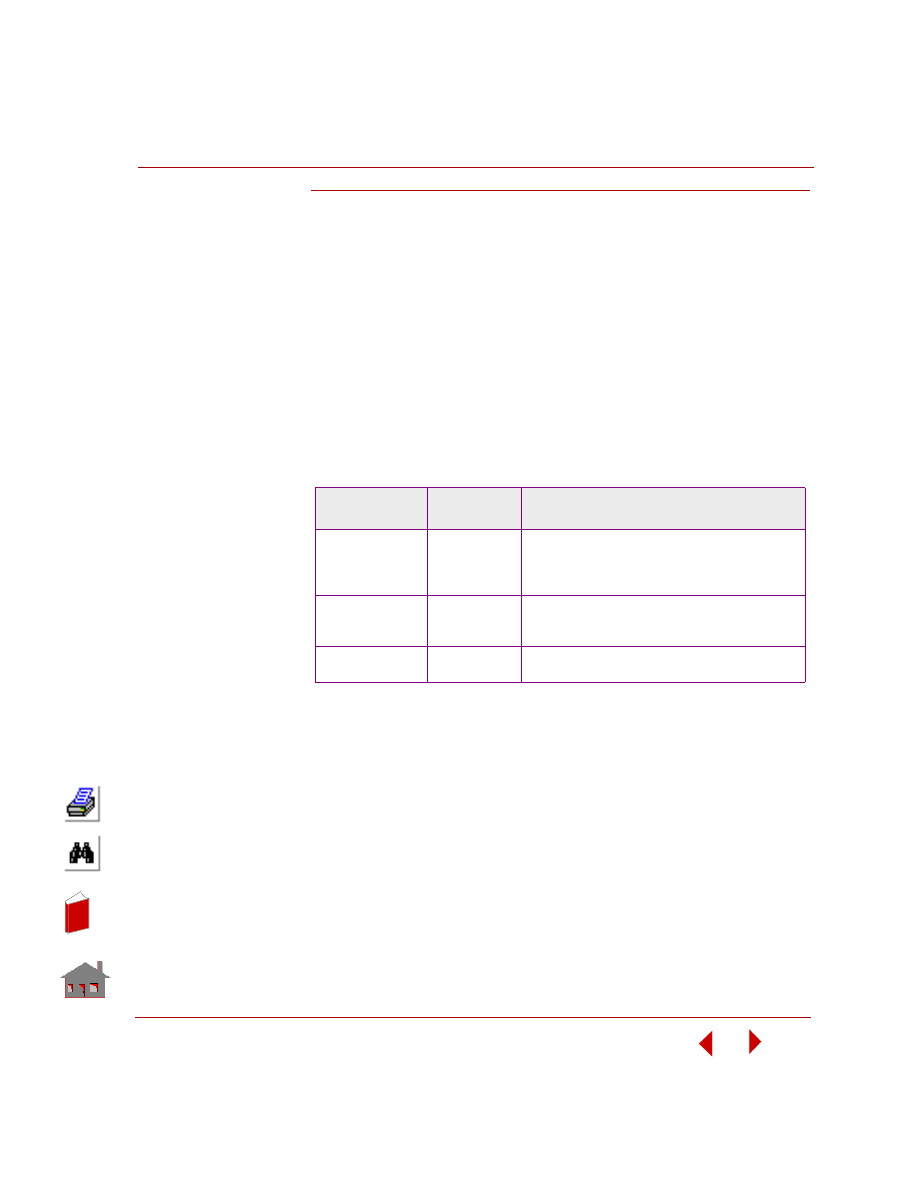
element model you build within GEOSTAR. The table below shows the commands
you can use in model verification and their functions.
Table 4-2. Commands for Model Input Verification
As you can notice from the above table, the
DATA_CHECK
command is a subset of
the
R_CHECK
command. Even though the
R_CHECK
command identifies
elements with bad geometry, the deletion of degenerate elements is performed by
the
ECHECK
command.
✍
You are strongly recommended to use the
R_CHECK
command and apply any
corrections to the finite element model before performing any analysis.
Note that the
R_CHECK
command is a general model verification tool. You may
still find some errors that are not trapped by the use of this command. In most cases,
the diagnostic messages either printed on the screen or written to an ASCII file
(*.CHK) provide further information as to the nature of error and its remedies.
Using the Menu
Typing the
Command
Function
Meshing
> ELEMENTS
> Check Element
ECHECK
Checks the aspect ratios of specified elements. The
command automatically deletes the degenerate
elements from the model. The command also
checks the element connectivities.
Analysis
> Data Check
DATA_CHECK
Checks if an element group, material property set,
and a real (section) constant have been defined for
each element in the model.
Analysis
> Run Check
R_CHECK
Performs rigorous checks on the model for validity
and completeness for the specified type of analysis.
In
de
x
In
de
x

4-8
COSMOSFFE Thermal
In
de
x
In
de
x

COSMOSFFE Thermal
5-1
5
Examples
Introduction
This chapter presents detailed examples for performing linear and nonlinear heat
transfer analysis using the COSMOSFFE Thermal module. The examples discussed
include large size practical problems as well as those of academic type for
verification purposes. Some benchmark results are also provided to demonstrate the
savings obtained in solution time and resources.
The following are some hints to assist you in performing a heat transfer analysis
using the COSMOSFFE Thermal module:
•
The
A_FFETHERMAL
(Analysis > HEAT TRANSFER >
FFE Thermal
Options
) command controls options of subsequent thermal analysis using the
FFE Thermal module. The
A_THERMAL
(Analysis > HEAT TRANSFER >
Thermal Analysis Options
) command controls options to be used by HSTAR,
the conventional heat transfer analysis module of COSMOSM.
•
If you are using the existing COSMOSM HSTAR input files for analysis in
COSMOSFFE Thermal, you need to use the
A_FFETHERMAL
command to
specify analysis options.
•
Information about used resources and the analysis module's messages are
written to an output file with .OUT
extension.
•
The
RESTART
(Analysis >
Restart
) command controls the restart option for
transient analysis.
In
de
x
In
de
x
Chapter 5 Examples
5-2
COSMOSFFE Thermal
Example Problems
Four examples are presented in the following pages. The first example discusses
steady-state linear heat transfer analysis using four different types of elements. The
second example deals with steady-state nonlinear heat transfer analysis due to
radiating boundary conditions. The next two examples represent problems with
large number of degrees of freedom to demonstrate the efficiency of COSMOSFFE.
Table 5-1. List of Thermal Examples
1 - Linear Heat Transfer Analysis
2 - Nonlinear Heat Transfer Analysis (Radiation)
3 - Linear Heat Transfer Analysis
4 - Linear Heat Transfer Analysis
In
de
x
In
de
x
COSMOSFFE Thermal
5-3
Chapter 5 Examples
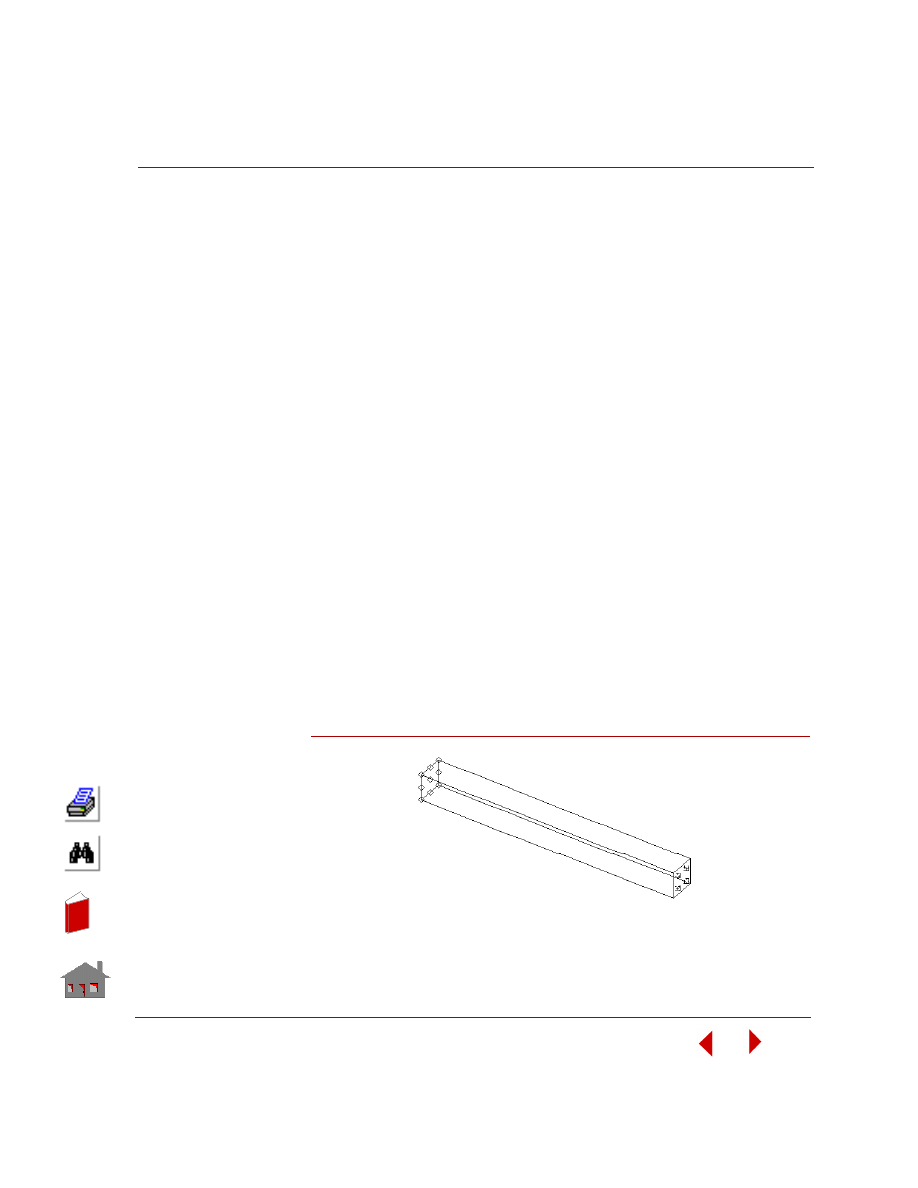
This example discusses linear steady-state heat transfer analysis in a 3D prismatic
model using four different types of elements: solid elements (SOLID, TETRA4)
and shell elements (SHELL4, SHELL3). When solid elements are used, the
prismatic model is assumed to be solid, and for using shell elements, the model is
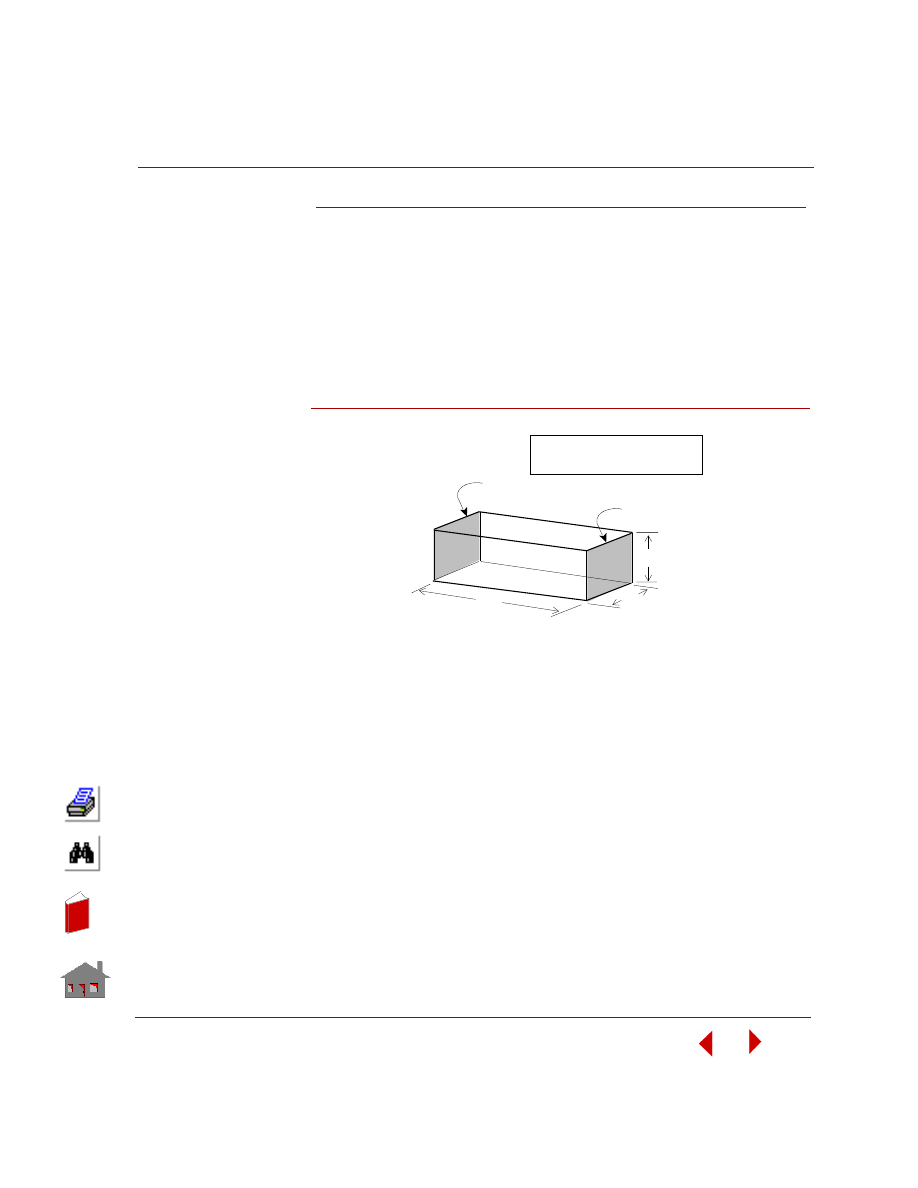
assumed to be hollow. The figure below shows the model geometry with material
properties and boundary conditions.
Figure 5-1. Problem Data and Geometry
The model geometry can be easily constructed by first building its cross section in
the Y-Z plane and then extruding it along the X-axis to form the 3D model. For
analysis using the solid elements, the entire solid will be meshed, whereas for
analysis using the shell elements, only the surfaces of the model will be meshed. To
start with, use the
SF4CORD
(Geometry > SURFACES >
Draw w/ 4 Coord
)
command from the menu tree with the coordinates as shown below:
Geo Panel: Geometry > SURFACES >
Draw w/ 4 Coord (SF4CORD)
Surface Label [1] >
1
XYZ coordinates of Keypoint 1 [0,0,0] >
0,0,0
XYZ coordinates of Keypoint 2 [0,0,0] >
0,50,0
XYZ coordinates of Keypoint 3 [0,0,0] >
0,50,50
XYZ coordinates of Keypoint 4 [0,0,0] >
0,0,50
Accept entries
Example 1 - Linear Heat Transfer Analysis
Thermal Conductivity = 1.0
0
°
10
°
50
100
50
In
de
x
In
de
x
Chapter 5 Examples
5-4
COSMOSFFE Thermal
Next, use the
VLEXTR
(Geometry > VOLUMES > GENERATION MENU >
Extrusion
) command to extrude the cross section along the X-axis as illustrated
below:
Geo Panel: Geometry > VOLUMES > GENERATION MENU >
Extrusion (VLEXTR)
Beginning Surface >
1
Ending Surface [1] >
Increment [1] >
Axis symbol [Z] >
X
Value >
100
Accept entries
With the geometry of the model now fully defined, you can proceed to generate the
finite element mesh. Four different cases will be solved using four different types of
elements as indicated in the table below:
Case A - Using Hexahedral Solid Elements (SOLID)
The
VLEXTR
command generates a solid volume entity in GEOSTAR which can be
meshed with lower order (8-node) hexahedral solid elements (SOLID) using the
M_VL
(Meshing > PARAMETRIC MESH >
Volumes
) command from the menu
tree (You have the option to use higher order elements during analysis by
specifying the appropriate flag under the
A_FFETHERMAL
command). The
number of elements along each curve of the volume entity are specified as shown
below:
Geo Panel: Meshing > PARAMETRIC MESH >
Volumes (M_VL)
Beginning Volume [1] >
Ending Volume [1] >
Increment [1] >
Number of nodes per element [8] >
Number of elements on first curve [2] >
15
Case
Element Type
No. of Nodes
No. of Elements
A
Solid hexahedral elements, second order
7936
6750
B
4-node shell elements, second order
2252
2250
C
3-node shell elements, second order
1002
2000
D
Solid tetrahedral elements, second order
951
3972
In
de
x
In
de
x

COSMOSFFE Thermal
5-5
Chapter 5 Examples
Number of elements on second curve [2] >
15
Number of elements on third curve [2] >
30
Accept all default values
The figure on the following page shows a view of the finite element mesh generated
without the hidden lines.
The applied thermal boundary conditions on the two faces of the model are
enforced using the command
NTSF
(LoadsBC > THERMAL > TEMPERATURE
>
Define by Surface
), shown below:
Geo Panel: LoadsBC > THERMAL > TEMPERATURE >
Define by Surface
(NTSF)
Beginning Surface >
1
Value >
10
Ending Surface [1] >
Increment [1] >
Click OK to accept entries
Repeat the
NTSF
command to apply the thermal boundary conditions at the other
end which is at a temperature of 0
°. The figure below shows the applied boundary
conditions.
Figure 5-2. Finite Element Mesh and Applied Thermal Boundary Conditions
The definition of the element type to be used in the analysis and the specification of
the material properties, illustrated below, complete the preparation of the finite
element model:
In
de
x
In
de
x

Chapter 5 Examples
5-6
COSMOSFFE Thermal
Geo Panel: Propsets >
Element Group (EGROUP)
Element group set label [1] >
1
Element Name >
SOLID
Click on Continue icon
Accept all default entries
Geo Panel: Propsets >
Material Property (MPROP)
Material property set [1] >
1
Material property name >
KX
Property value >
1.0
Click on OK icon
Click Cancel to end this command
Before proceeding to perform the heat transfer analysis, you need to specify the
appropriate flags for analysis using the
A_FFETHERMAL
(Analysis > HEAT
TRANSFER >
FFE Thermal Options
) command as illustrated below:
Geo Panel: Analysis > HEAT TRANSFER >
FFE Thermal Options
(A_FFETHERMAL)
Analysis option [S: Steady] >
Element order 1=First 2=Second [2] >
Convergence tolerance [0.001] >
Unused option >
Formulation flag 0=lump 1=cons >
Click OK to accept entries
The options selected above specify steady state heat transfer analysis using second
order elements. The command
R_THERMAL
(Analysis > HEAT TRANSFER >
Run Thermal Analysis
) can now be used to execute analysis. After successful
completion of analysis, you can proceed to postprocess the results.
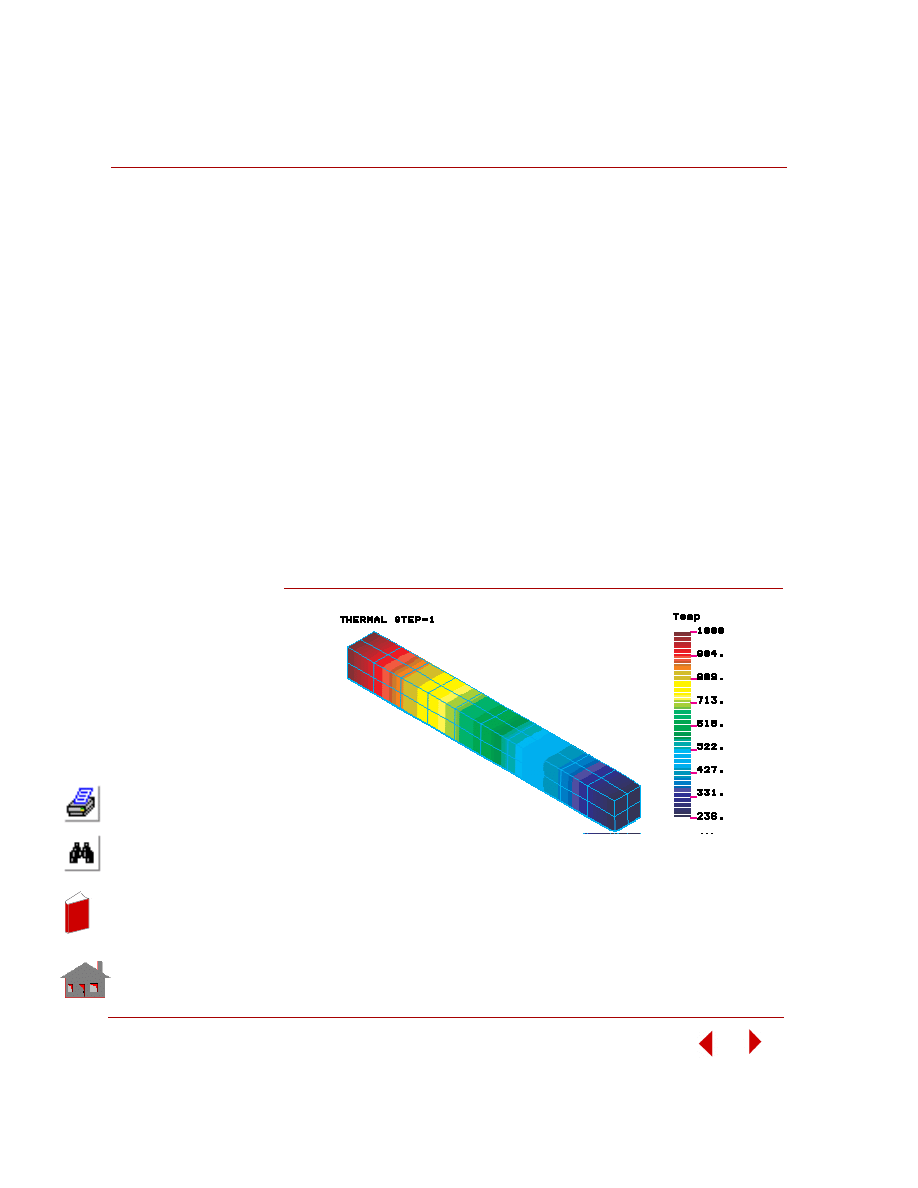
In order to graphically view the temperature distribution (Figure 5-3), follow the
steps given below using the menu tree:
Geo Panel: Results > PLOT >
Thermal
Time step number [1] >
1
Component [TEMP] >
TEMP: Nodal Temperature
Select Contour Plot
Click OK to apply default entries
In
de
x
In
de
x

COSMOSFFE Thermal
5-7
Chapter 5 Examples
If the user preferred to type in the commands using the keyboard, two commands
should be typed in:
GEO >
ACTTEMP;
GEO >
TEMPLOT;
Figure 5-3. Temperature Contour Plot
The solution time data for the problem can be obtained from the output file
(jobname.OUT).
Case B - Using Quadrilateral Shell Elements (SHELL4)
Delete the mesh using the command
MVLDEL
(Edit > DELETE >
Element on
Volume
) and select the
M_SF
(Meshing > PARAMETRIC MESH >
Surfaces
)
command to mesh only the surfaces of the model. To begin with, select the end
faces (surfaces 1 and 2), and in the second attempt, select the side faces (surfaces 3
through 6). For the end faces, specify the number of elements as 15 along each
curve. For the side faces, specify 15 elements along the shorter curve, and 30
elements along the longer curve. When you are meshing these surfaces, specify
In
de
x
In
de
x

Chapter 5 Examples
5-8
COSMOSFFE Thermal
lower order elements (4-noded elements in this case). Since the mesh is generated
independently for each surface, you need to use the
NMERGE
(Meshing > NODES
>
Merge
) and
NCOMPRESS
(Edit >
Compress Nodes
) commands from the menu
tree to merge the nodes and remove node numbering gaps respectively, in order to
satisfy the compatibility requirements.
You need to redefine the element group, specifying SHELL4 with default options.
You also need to specify a thickness of 0.1 for this element using the
RCONST
(Propsets >
Real Constant
) command with entries shown below:
Geo Panel: Propsets >
Element Group
EGROUP,1,SHELL4;
Geo Panel: Propsets >
Real Constant
RCONST,1,1,1,6,0.1;
Use the
NTSF
command as before to apply the thermal boundary conditions at the
two end faces. The analysis options set by the
A_FFETHERMAL
command still
remain valid, with second order solutions specified for this case also. The command
R_THERMAL
can now be used to execute the analysis. As before, you can view the
temperature contour plot. You will notice that the contours are the same as those
obtained using solid hexahedral elements.
Case C - Using Triangular Shell Elements (SHELL3)
Delete the mesh using the command
MSFDEL
(Edit > DELETE >
Element on
Surface
). We will use the 3D automatic meshing feature for polyhedron in this
case. From the Geometry > POLYHEDRA menu tree, select the
Define (PH)
command and generate a polyhedron out of the available surfaces as follows:
Geo Panel: Geometry > POLYHEDRA >
Define (PH)
Label of polyhedron [1] >
1
Reference entity name [RG] >
SF
Then accept
Surface label [1] >
1
Average element size >
5
Accept all entries
Next, from the Meshing > AUTO MESH menu tree, select the
Polyhedra (MA_PH
)
command to generate a mesh of triangular elements. This command by default
generates lower order elements.
In
de
x
In
de
x

COSMOSFFE Thermal
5-9
Chapter 5 Examples
You also need to redefine the element group, specifying SHELL3 with default
options. You need to specify a thickness of 0.1 using the
RCONST
command as
used before.
EGROUP,1,SHELL3;
RCONST,1,1,1,6,0.1;
Use the
NTSF
command as before to apply the thermal boundary conditions at the
two end faces. The analysis options set by the
A_FFETHERMAL
command still
remain valid, with second order solutions specified for this case also. The command
R_THERMAL
can now be used to execute analysis. As before, you can view the
temperature contour plot.
Case D - Using Tetrahedral Solid Elements (TETRA4)
Delete the mesh using the command
MSFDEL
(Edit > DELETE >
Element on
Surface
) from the menu tree. We will use the 3D automatic meshing feature for
part entities in this case. From the Edit > DELETE menu tree, select the
Polyhedra
(PHDEL)
command and delete the polyhedron defined earlier. Re-execute the
PH
command and specify an average element size of 7.5. Alternately, you can use the
PHDENSITY
(Meshing > MESH DENSITY >
Polyhedron Elem Size
) command to
redefine the mesh density of a polyhedron. To define a solid entity, you need to use
the
PART
(Geometry >
Define Part
) command. Next, from the Meshing > AUTO
MESH menu tree, select the command
Parts (MA_PART)
to generate a mesh of
tetrahedral elements.
You also need to redefine the element group, specifying TETRA4 with default
options.
EGROUP,1,TETRA4;
Use the
NTSF
command as before to apply the thermal boundary conditions at the
two end faces. The analysis options set by the
A_FFETHERMAL
command still
remain valid, with second order solutions specified for this case also. The command
R_THERMAL
can now be used to execute analysis. As before, you can view the
temperature contour plot.
In
de
x
In
de
x
Chapter 5 Examples
5-10
COSMOSFFE Thermal
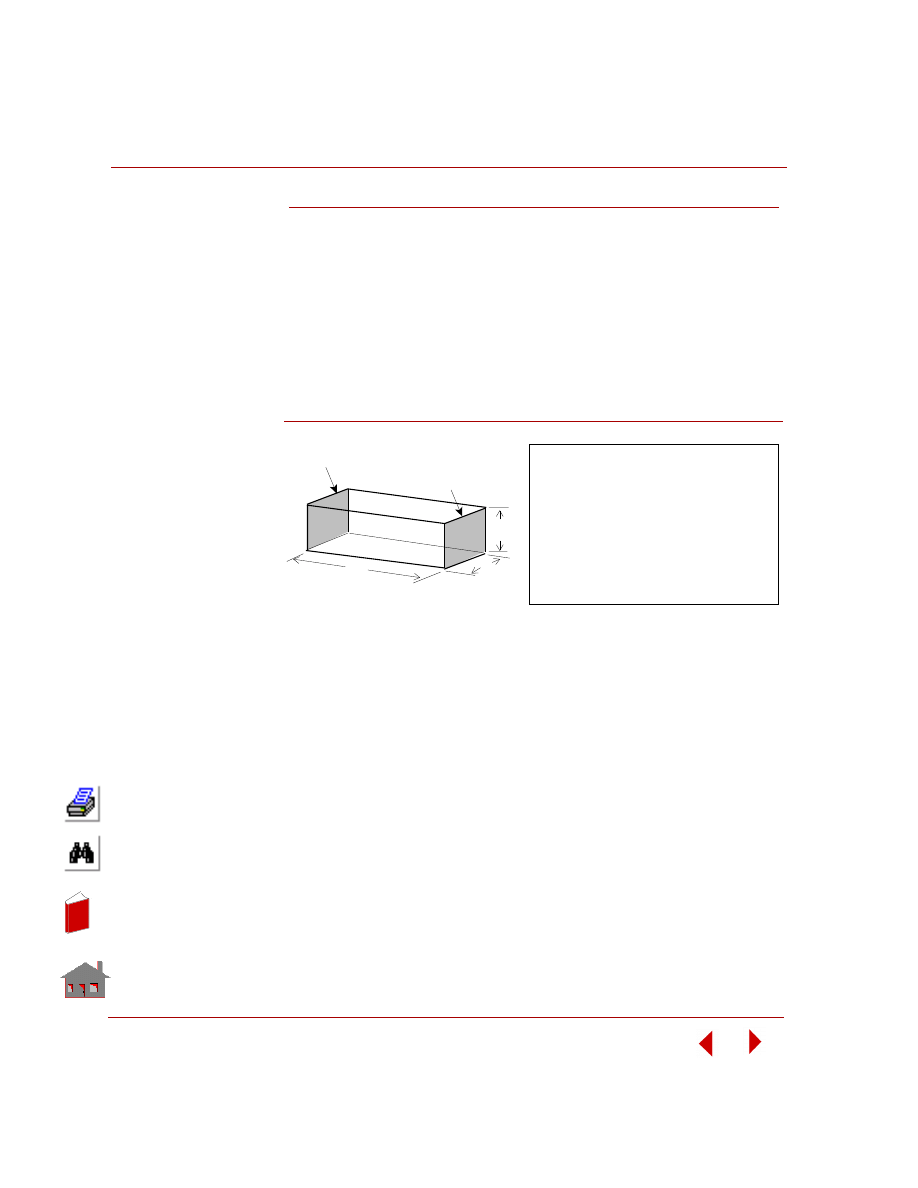
This example discusses the nonlinear steady-state heat transfer analysis in a
prismatic 3D solid which has a prescribed temperature at one end, and the other end
is radiating heat into the ambient atmosphere with a temperature of 10
°C. The 1D
version of this example is provided to you as a verification problem (TN03) and is
discussed in the next chapter. The figure below shows the geometry and boundary
conditions of the solid.
Figure 5-4. Problem for Analysis
The finite element mesh of this problem can be easily created by first constructing a
surface in the X-Y plane along the length of the solid and meshing it with
quadrilateral plane elements. The surface and its mesh can be then extruded in the
Z-direction to form the 3D solid with brick elements.
In order to create a surface with corners at (0,0), (10,0), (10,1), and (0,1), use the
SF4CORD
(Geometry > SURFACES >
Draw w/ 4 Coord
) command as shown
below:
Geo Panel: Geometry > SURFACES >
Draw w/ 4 Coord (SF4CORD
)
Surface label [1] >
1
XYZ coordinates of Keypoint 1 [0,0,0] >
0,0,0
XYZ coordinates of Keypoint 2 [0,0,0] >
10,0,0
XYZ coordinates of Keypoint 3 [0,0,0] >
10,1,0
XYZ coordinates of Keypoint 4 [0,0,0] >
0,1,0
Accept entries
Example 2 - Nonlinear Heat Transfer Analysis
(Radiation)
Length of the Rod
Area of cross section
Thermal conductivity
Ambient temperature
Prescribed temp. at left end
= 10.0 m
= 1.0 m
= K = 45.0 W/m
°
C
= T
= 10.0
°
C
= T = 1000
°
C
Radiation Data:
Area of radiating surface
View factor
Emissivity
Stefan-Boltzmann constant
= 1.0 m
= 1.0
= 1.0
= 5.67E-8 W/m
°
K
0
∞
2
4
2
2
T = 1000
°
C
T = 10
°
C
∞
Radiation
1
10
1
In
de
x
In
de
x

COSMOSFFE Thermal
5-11
Chapter 5 Examples
The surface created can be now meshed with quadrilateral elements using the
M_SF
(Meshing > Parametric Mesh >
Surfaces
) command as shown below:
Geo Panel: Meshing > PARAMETRIC MESH >
Surfaces (M_SF)
Beginning surface [1] >
1
Ending surface [1] >
1
Increment [1] >
1
Number of nodes per element [4] >
4
Number of elements on 1st curve [2] >
10
Number of elements on 2nd curve [2] >
2
Accept default values for spacing ratio
Click OK
The figure below shows the plot of the surface and the elements generated for
extrusion to form the 3D solid.
Figure 5-5. Surface and its Mesh for Extrusion
In GEOSTAR, extrusions are performed on geometric entities. Therefore, before
you extrude the generated mesh in the Z-direction to form the 3D mesh, you need to
activate the flag for carrying the mesh with geometry using the command
ACTDMESH
(Control > ACTIVATE >
Default Meshing
):
Geo Panel: Control > ACTIVATE >
Default Meshing (ACTDMESH)
Entity >
VL
Default mesh Flag 0=off 1=on [1] >
Accept entries
Next, apply the command
VLEXTR
(Geometry > VOLUMES > GENERATION
MENU >
Extrusion
) to extrude the surface and its mesh to form the 3D solid with
In
de
x
In
de
x

Chapter 5 Examples
5-12
COSMOSFFE Thermal
brick elements as illustrated below. We will use two layers of elements along the Z-
direction.
Geo Panel: Geometry > VOLUMES > GENERATION MENU >
Extrusion
(VLEXTR)
Beginning Surface [1] >
1
Ending Surface [1] >
Increment [1] >
Axis symbol [Z] >
Value >
1
Number of layers of elements [4] >
2
Original mesh update flag [1] >
Accept entries
The figure below shows plots of the mesh obtained by extrusion with and without
hidden lines.
Figure 5-6. Finite Element Mesh of the Solid Obtained by Extrusion
The prescribed temperature of 1000
°C at the left end is applied using the
NTSF
(LoadsBC > THERMAL > TEMPERATURE >
Define by Surface
) command as
illustrated below:
Geo Panel: LoadsBC > THERMAL > TEMPERATURE >
Define by Surface
(NTSF)
Beginning Surface [1] >
4
Value >
1000
Ending Surface [1] >
4
Increment [1] >
Click OK to accept entries
In
de
x
In
de
x
COSMOSFFE Thermal
5-13
Chapter 5 Examples
The radiation boundary conditions at the right end are enforced using the
RESF
(LoadsBC > THERMAL > RADIATION >
Define
) command as shown below:
Geo Panel: LoadsBC > THERMAL > RADIATION >
Define by Surface
(RESF)
Beginning Surface [1] >
6
Emissivity Coefficient [1] >
1
View factor [1] >
Source temperature >
10
Ending Surface >
6
Increment [1] >
Time curve for source temperature [0] >
Click OK to accept entries
The Stefan-Boltzmann constant required for radiation calculations is specified
using the
SB_CONST
(Analysis > HEAT TRANSFER >
Stefan-Boltzmann
Constant
) command. The command and its input are shown below:
Geo Panel: Analysis > HEAT TRANSFER >
Stefan-Boltzmann Constant
(SB_CONST)
Stefan-Boltzmann constant >
5.67E-8
Click OK to accept entry
To specify the difference between the absolute zero and the zero of the temperature
scale used, the
TOFFSET
(Analysis > HEAT TRANSFER >
Offset Temperature
)
command is used with an offset value of 273.15.
The temperature and radiation boundary conditions applied on the prismatic solid
are shown in the figure below.
Figure 5-7. Applied Thermal Boundary Conditions
In
de
x
In
de
x
Chapter 5 Examples
5-14
COSMOSFFE Thermal
The definition of the element type to be used in the analysis and the specification of
the material properties, illustrated below, are defined using the Propsets menu tree
to complete the preparation of the finite element model:
EGROUP,1,SOLID;
MPROP,1,KX,45;
Before proceeding to perform the heat transfer analysis, you need to specify the
appropriate flags for analysis using the
A_FFETHERMAL
(Analysis > HEAT
TRANSFER >
FFE Thermal Options
) command with default entries.
The command
R_THERMAL
(Analysis > HEAT TRANSFER >
Run Thermal
Analysis
) can now be used to execute analysis. After successful completion of
analysis, you can proceed to postprocess the results. The figure below shows
temperature contours obtained by using the Results > PLOT >
Thermal
menu tree
according to the procedure described in the previous example.
The theoretical solution for this problem is provided in the next chapter (see TN03).
The computed temperature at the radiating surface is 235.77 which exactly matches
with the analytical solution, 235.77.
Figure 5-8. Temperature Contours
In
de
x
In
de
x

COSMOSFFE Thermal
5-15
Chapter 5 Examples
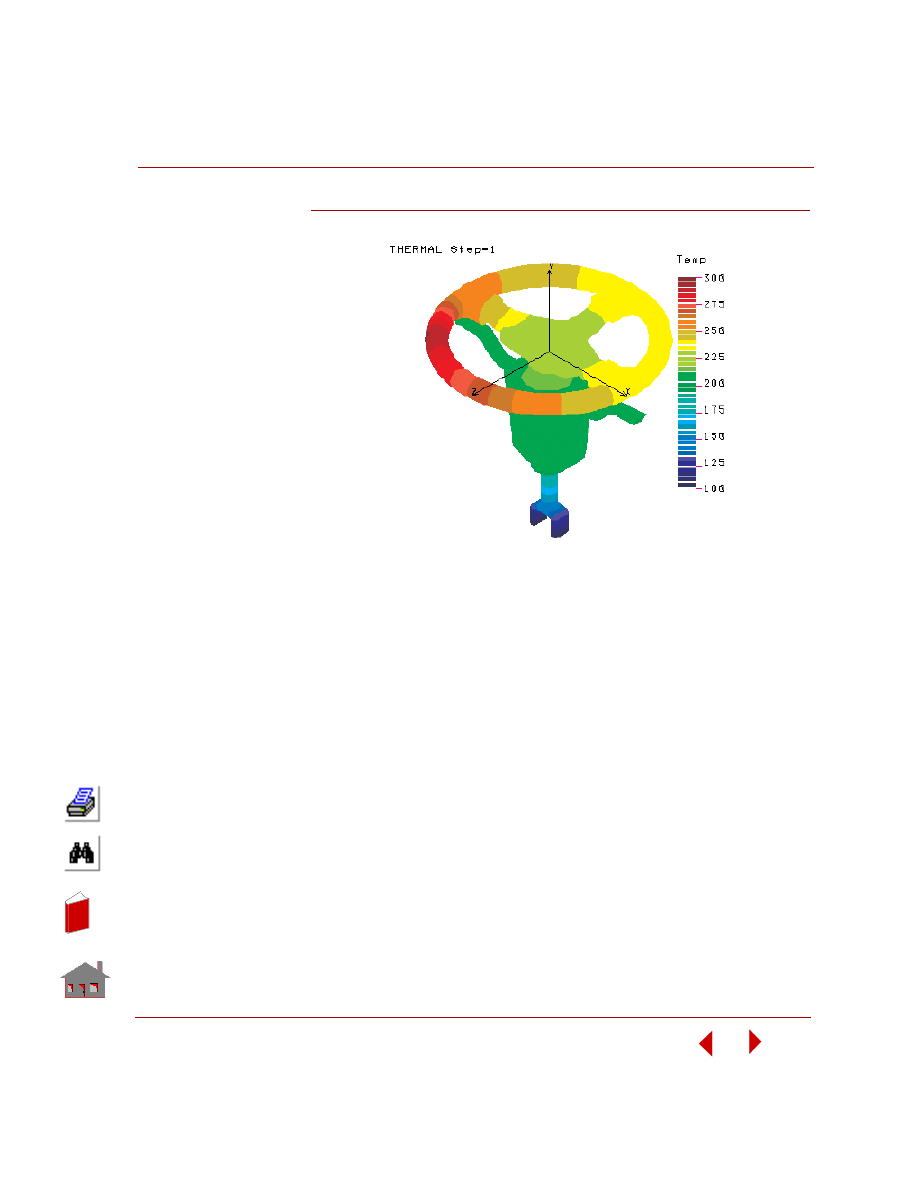
This example has been provided to function as a large size problem for solution.
The input for this example is available in the file SSW55.GEO which can be found
in ExampleProblems subdirectory of your COSMOSM directory. The model for
steady-state analysis consists of an automobile steering assembly. There are 5445
nodes and 20407 tetrahedral elements in this problem. The material of the steering
assembly has a unit thermal conductivity. The thermal boundary condition for this
problem consists of an applied nodal temperature of 300 degrees at nodes 1224,
1225, 1269, 1474, and 1475. The finite element model of the steering assembly is
shown in the figure below.
Copy the file SSW55.GEO
to your working directory
and start a new problem.
From the File >
Load...
menu, you may select or
enter the input file name as
SSW55.GEO. This is
equivalent to typing the
command
FILE
using the
keyboard. The input file
consists of finite element
model data, and is about 1.2
MB in size. You may
therefore choose to turn off
the display, echo, and log
option flags.
After the input file is
completely read, you can
view the model using the
EPLOT
(Edit > PLOT >
Elements
) command. Use
Example 3 - Linear Heat Transfer Analysis
Figure 5-9. Finite Element Model of the Steering
Assembly for Analysis.
In
de
x
In
de
x

Chapter 5 Examples
5-16
COSMOSFFE Thermal
the commands
NTLIST
(LoadsBC > THERMAL > TEMPERATURE >
List
),
MPLIST
(Edit > LIST >
Material Props
), and
EGLIST
(Edit > LIST >
Element
Groups
), to verify the applied nodal temperatures, the defined material properties,
and the selected element group for analysis, respectively.
Since the finite element model is completely defined, you can proceed to
performing the analysis. In order to specify the appropriate analysis flags, use the
A_FFETHERMAL
(Analysis > HEAT TRANSFER >
FFE Thermal Options
)
command with default entries.
The command
R_THERMAL
can now be used to execute analysis. After successful
completion of analysis, you can proceed to postprocess the results. In order to
graphically view the temperature distribution (Figure 5-10), follow the steps given
below using the menu tree:
Geo Panel: Display > DISPLAY OPTION >
Eval Element Bound
Boundary face evaluation >
Yes
Boundary edge evaluation >
Yes
Tolerance angle to ignore curvature (for edge) >
20
Evaluation criterion (for edge) >
Mesh
Click OK to accept
Geo Panel: Results > PLOT >
Thermal
Time step number [1] >
1
Component [TEMP] >
TEMP: Nodal Temperature
Select Contour Plot
Click OK to accept
If the user preferred to type in the commands using the keyboard, two commands
should be typed in:
GEO >
ACTTEMP;
GEO >
TEMPPLOT;
In
de
x
In
de
x
COSMOSFFE Thermal
5-17
Chapter 5 Examples
Figure 5-10. Temperature Contours
In
de
x
In
de
x

Chapter 5 Examples
5-18
COSMOSFFE Thermal
This example has been provided to function as a large size problem for solution.
The input for this example is available in the file PTC1.GEO which can be found in
the ExampleProblems subdirectory of your COSMOSM directory. The model for
steady-state analysis consists of a machine component. There are 3,590 nodes and
10,994 tetrahedral elements in this problem. The material of the steering assembly
has a unit thermal conductivity. The thermal boundary conditions for this problem
consist of an applied nodal temperature of 20 degrees on the top face, and the
bottom face is subjected to convective boundary conditions with a unit film
coefficient. The ambient temperature for convection is 50 degrees. The finite
element model with the applied thermal boundary conditions is shown in the figure
below.
Copy the file PTC1.GEO to
your working directory and
start a new problem. From the
File >
Load...
menu, you may
select or enter the input file
name as PTC1.GEO. This is
equivalent to typing the
command
FILE
using the
keyboard. The input file
consists of finite element
model data, and is about 0.7
MB in size. You may therefore
choose to turn off the display,
echo, and log option flags:
After the input file is
completely read, you can view
the model using the
EPLOT
(Edit > PLOT >
Elements
)
command. Use the commands
NTLIST
(LoadsBC > THERMAL > TEMPERATURE >
List
),
CELIST
(LoadsBC >
THERMAL > CONVECTION >
List
),
MPLIST
(Edit > LIST >
Material Props
),
and
EGLIST
(Edit > LIST >
Element Groups
), to verify the applied nodal
temperatures, convective boundary conditions, material properties defined, and the
element group selected for analysis, respectively.
Example 4 - Linear Heat Transfer Analysis
Figure 5-11. Finite Element Model for Analysis
In
de
x
In
de
x

COSMOSFFE Thermal
5-19
Chapter 5 Examples
Since the finite element model is completely defined, you can proceed to
performing the analysis. In order to specify the appropriate analysis flags, use the
A_FFETHERMAL
(Analysis > HEAT TRANSFER >
FFE Thermal Options
)
command with default entries.
The command
R_THERMAL
can now be used to execute analysis. After successful
completion of analysis, you can proceed to postprocess the results. In order to
graphically view the temperature distribution (Figure 5-12), follow the steps given
below using the menu tree:
Geo Panel: Display > DISPLAY OPTION >
Eval Element Bound
Boundary face evaluation >
Yes
Boundary edge evaluation >
Yes
Tolerance angle to ignore curvature (for edge) >
20
Evaluation criterion (for edge) >
Mesh
Click OK to accept
Geo Panel: Results > PLOT >
Thermal
Time step number [1] >
1
Component [TEMP] >
TEMP: Nodal Temperature
Select Contour Plot
Click OK to accept
If the user preferred to type in the commands using the keyboard, two commands
should be typed in:
GEO >
ACTTEMP;
GEO >
TEMPPLOT;
In
de
x
In
de
x

Chapter 5 Examples
5-20
COSMOSFFE Thermal
Figure 5-12. Temperature Contours
In
de
x
In
de
x
COSMOSFFE Thermal
6-1
6
Verification Problems
Introduction
In the following, a comprehensive set of benchmark problems are provided to
illustrate the various features of the COSMOSFFE heat transfer analysis module.
The problems are carefully selected to cover a wide range of applications in the
field of thermal analysis.
The input files for FFE problems are available in “...\Vprobs\FFE” folder in the
COSMOS installation directory. Where “...” refers to the directory in which you
installed COSMOSM. You may copy the desired input file into your working
directory, create a new problem, and then use the
File
(File >
Load...
) command to
read the input file and to run the problem.
In
de
x
In
de
x

Chapter 6 Verification Problems
6-2
COSMOSFFE Thermal
Table 6-1. List of Verification Problems
Problem
Element
Title
FFETL01
SHELL3T
Steady State Heat Conduction in a Square Plate
FFETL02
SHELL4
Steady State Heat Conduction in an Orthotropic
Plate
FFETL03
PLANE2D
Transient Heat Conduction in a Long Cylinder
FFETL04
PLANE2D
Thermal Stresses in a Hollow Cylinder
FFETL05
PLANE2D
Heat Conduction Due to a Series of Heating
Cables
FFETL08
TRUSS2D
Transient Heat Conduction in a Slab of Constant
Thickness
FFETL09
TRUSS, CLINK
Heat Transfer from Cooling Fin
FFETN01
TRUSS2D
Heat Conduction with Temperature Dependent
Conductivity
FFETN03
TRUSS2D, RLINK
Radiation in a Rod
In
de
x
In
de
x

COSMOSFFE Thermal
6-3
Chapter 6 Verification Problems
TYPE:
Steady-state heat conduction with prescribed temperature boundary conditions,
SHELL3T elements are used.
REFERENCE:
Carslaw, H. S., and Jaeger, J. C., “Conduction of Heat in Solids,” 2nd Edition,
Oxford University Press, 1959.
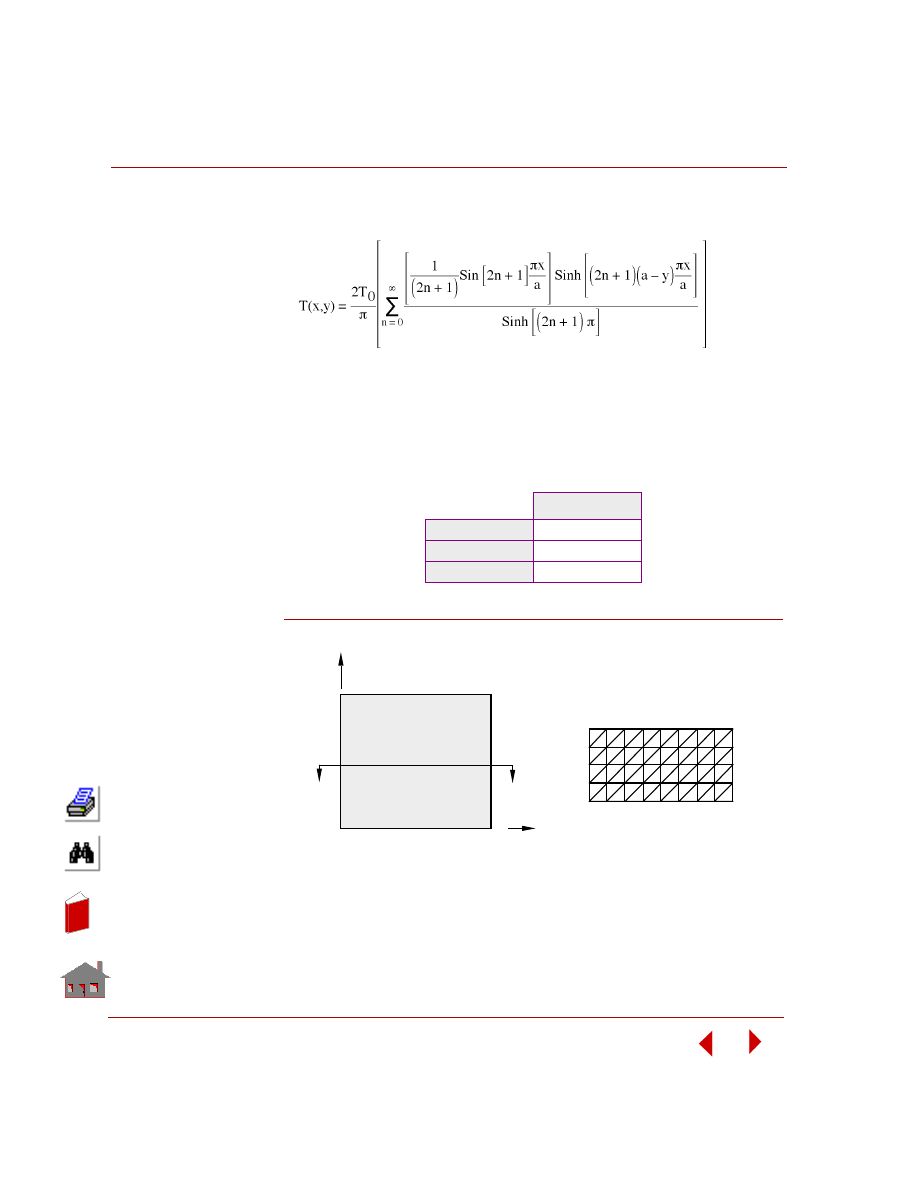
PROBLEM:
Determine the temperature at the center of a square plate with prescribed edge
temperatures.
GIVEN:
Thermal Conductivity = 43 w/m
°C
Width and Height of Plate = 4 m
Boundary Conditions:
Along the edge AB, temp. = 0
° C
Along the edge BC, temp. = 0
° C
Along the edge CD, temp. = 0
° C
Along the edge DA, temp. = 100
° C
MODELING HINTS:
Since the plate and boundary conditions are symmetrical about I-I, only one half of
the plate is modeled using SHELL3T elements as shown in the figure.
FFETL01: Steady State Heat Conduction in a
Square Plate
In
de
x
In
de
x
Chapter 6 Verification Problems
6-4
COSMOSFFE Thermal
ANALYTICAL SOLUTION:
Temperature at any point (x,y) in the plate is
Where
a
= The length of a side of plate
T
0
= The temperature at x = 0
COMPARISON OF RESULTS:
At the center of the plate (Node 41).
Figure FFETL01–1.
Temperature
°
C
Theory
25.0
COSMOSFFE
24.99
Difference
0.04%
39
38
40
37
Y
C
D
X
A
B
I
I
0
°
0
°
0
°
100
°
1
2
3
4
5
41
6
42
7
43
8
44
9
45
28
36
19
27
10
18
Problem Sketch
Finite Element Model
In
de
x
In
de
x

COSMOSFFE Thermal
6-5
Chapter 6 Verification Problems
TYPE:
Steady-state heat conduction with convection boundary conditions, SHELL4
elements.
REFERENCE:
M. N. Ozisik, “Heat Conduction,” Wiley, New York, 1980.
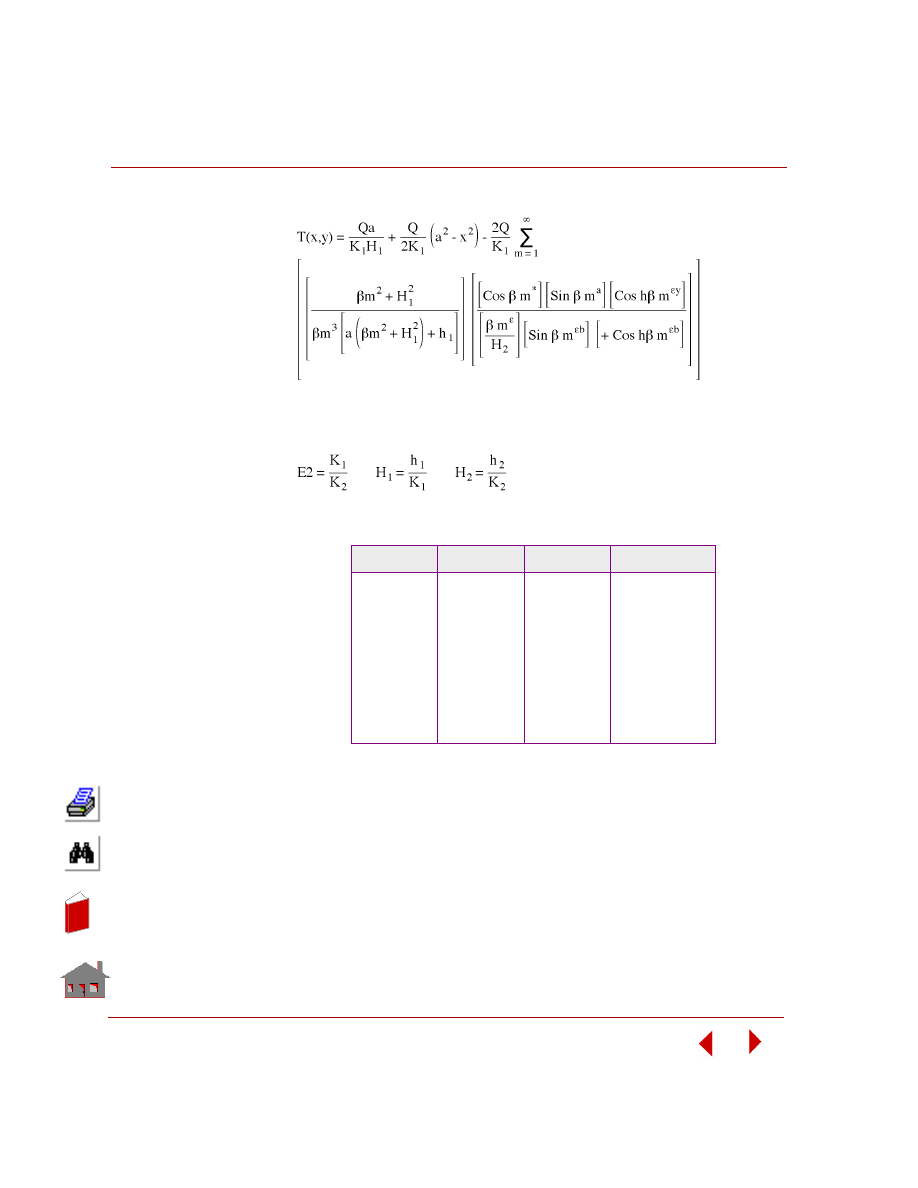
PROBLEM:
Determine the temperature distribution in an orthotropic plate with a constant rate of
heat generation. The boundaries at x=0 and y=0 are insulated, and those at x=a and
y=b are dissipating heat by convection into the atmosphere which is at zero
temperature.
GIVEN:
Thermal Conductivity along x direction = k
x
= 10 W/m
°C
Thermal Conductivity along y direction = k
y
= 20 W/m
°C
Convection heat transfer coefficient at the boundary BC = h
1
= 10 W/m
2
°C
Convection heat transfer coefficient at the boundary DC = h
2
= 20 W/m
2
°C
Length of the plate = a = 1.0 m
Width of the plate = b = 2.0 m
Thickness of the plate = 0.1 m
Rate of heat generation Q = 100 W/m
3
MODELING HINT:
Plate is modeled using 200 SHELL4 elements.
FFETL02: Steady State Heat Conduction in an
Orthotropic Plate
In
de
x
In
de
x
Chapter 6 Verification Problems
6-6
COSMOSFFE Thermal
ANALYTICAL SOLUTION:
Where:
K
1
= K K
2
= Ky
COMPARISON OF RESULTS:
Node
X (m)
Theory
COSMOSFFE
111
112
113
114
115
116
117
118
119
120
121
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
8.5094
8.4832
8.4045
8.2728
8.0874
7.8471
7.5505
7.1959
6.7811
6.3038
5.7613
8.5102
8.4840
8.4053
8.2737
8.0882
7.8479
7.5513
7.1967
6.7819
6.3046
5.7620
In
de
x
In
de
x
COSMOSFFE Thermal
6-7
Chapter 6 Verification Problems
Figure FFETL02–1.
b
Insulated
Insulated
a
221
231
1
11
y
x
Problem Sketch
Finite Element
Model
A
B
C
D
T = 0
°
C
h = 20 w/m
°
C
2
2
∞
T = 0
°
C
h = 10 w/m
°
C
2
1
∞
In
de
x
In
de
x

Chapter 6 Verification Problems
6-8
COSMOSFFE Thermal
TYPE:
Transient heat conduction with convection boundary conditions, PLANE2D
elements.
REFERENCE:
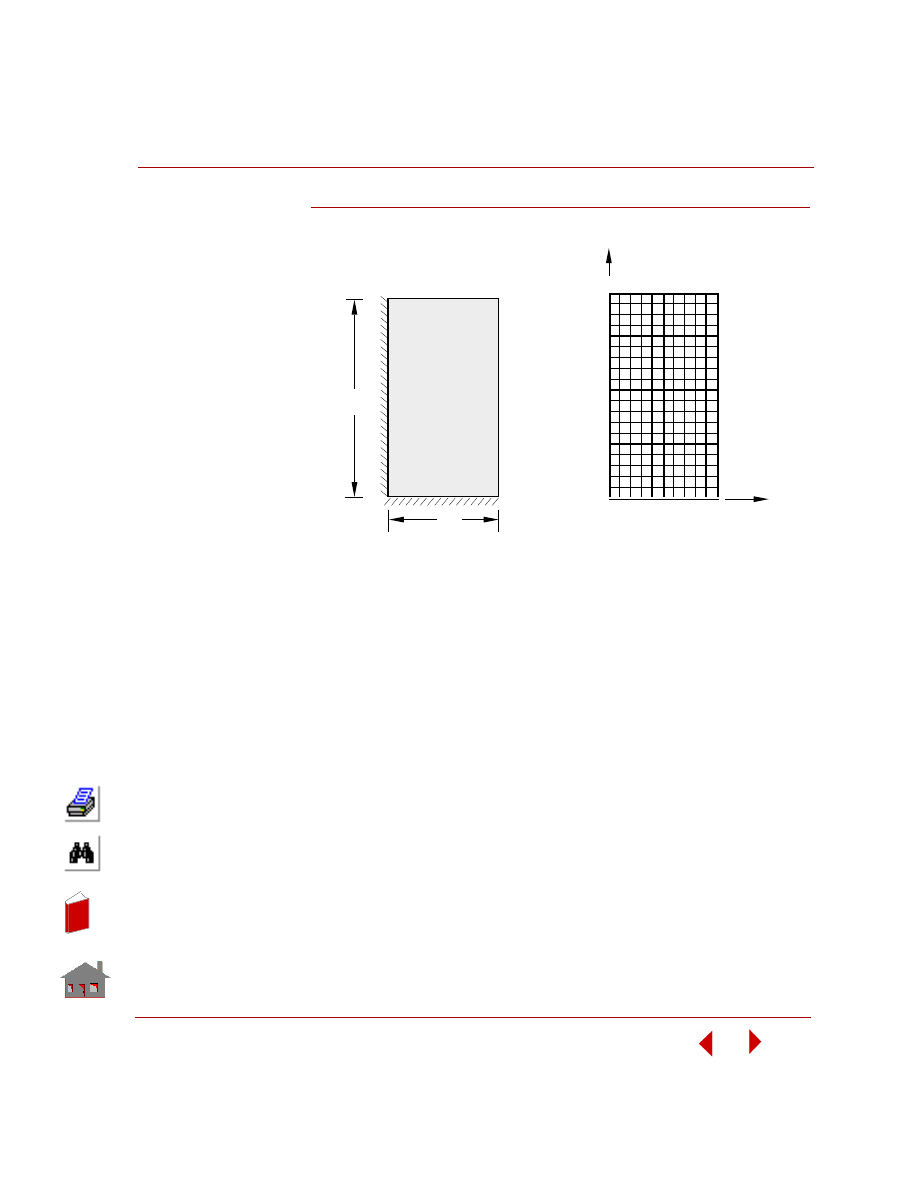
J. P. Holman, “Heat Transfer,” McGraw-Hill Book Company, 1976, p. 117.
PROBLEM:
A long aluminum cylinder, 5.0 cm in diameter and initially at 200
° C, is suddenly
exposed to a convection environment at 70
° C and h = 525 W/m
2
°C. Calculate the
temperature at a radius of 1.25 cm, one minute after the cylinder is exposed to the
environment.
GIVEN:
Radius of cylinder = r
o
= 0.025m
Thermal conductivity = K = 215.0 W/m
°C
Mass density =
ρ = 2700.0 kg/m
3
Specific heat = C = 936.8 J/Kg
°C
Initial temperature = T
0
= 200
° C
Convective heat
transfer coefficient = h = 525 w/m
2
°C
Ambient temperature = T
∞
= 70
° C
MODELING HINTS:
Since the cylinder and boundary conditions are axisymmetric, PLANE2D
axisymmetric elements are used to model this problem.
FFETL03: Transient Heat Conduction in a Long
Cylinder
In
de
x
In
de
x
COSMOSFFE Thermal
6-9
Chapter 6 Verification Problems
COMPARISON OF RESULTS:
Comparison of solutions is made at r = 0.0125 m (node 21) and at t = 60 sec.
Figure FFETL03–1.
Temperature
°
C
Theory
118.4
COSMOSFFE
119.49
h, T
8
X
Z
Problem Sketch
r
o
Y
2
6
4
40
42
41
39
1
5
3
Y
Finite Element Model
X
1
2
r
o
In
de
x
In
de
x

Chapter 6 Verification Problems
6-10
COSMOSFFE Thermal
TYPE:
Thermal stress analysis, PLANE2D axisymmetric element.
REFERENCE:
Timoshenko and Goodier, “Theory of Elasticity,” McGraw-Hill Book Co., New
York, 1961.
PROBLEM:
The hollow cylinder in plane strain is subjected to two independent loading
conditions.
1.
An internal pressure P
a
2.
A steady state axisymmetric temperature distribution due to the following
boundary conditions.
At r = 1.0, temperature = 100
At r = 2.0, temperature = 0
GIVEN:
E
= 30 x 10
6
psi
a
= 1 in
b
= 2 in
ν =
0.3
α
x
=
1*10
-6
/
°F
K
x
= 1 BTU/in S
°F
P
a
=
100
psi
T
a
=
100
° F
T
b
=
0
° F
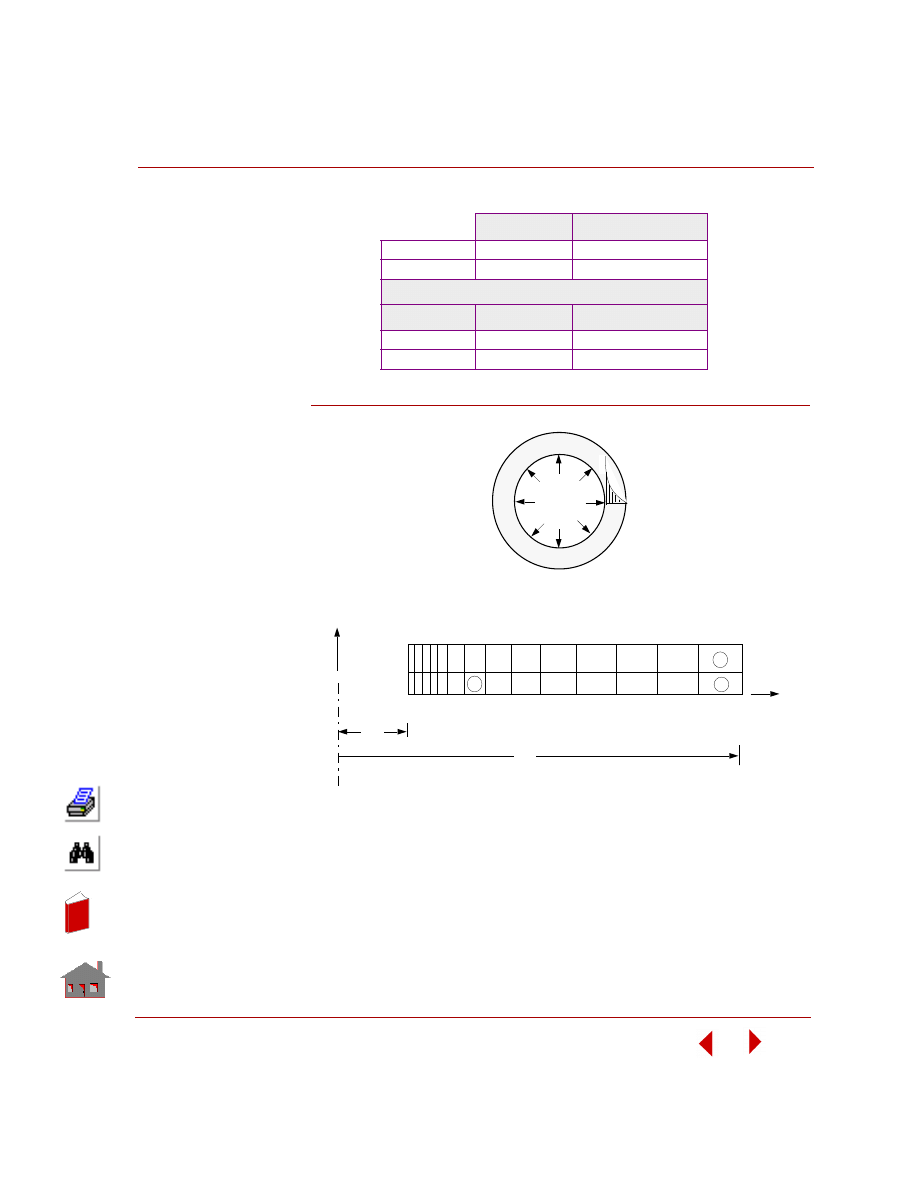
✍
The COSMOSM STAR module is required in addition to FFE Thermal, to solve
this problem.
FFETL04: Thermal Stresses in a Hollow Cylinder
In
de
x
In
de
x
COSMOSFFE Thermal
6-11
Chapter 6 Verification Problems
COMPARISON OF RESULTS:
Figure FFETL04–1.
Theory
COSMOSFFE
Node 23
°
F
59.401
59.401
Node 42
°
F
23.447
23.447
Stresses in Element 7 (Center)
Theory
COSMOSM STAR
T
r
-398.34
-398.14
T
θ
-592.47
-596.38
L
Problem Sketch
Ta
Pa
Tr
15
14
28
1 2 3
12
45
x
y
b
31
8
7
30
C
Finite Element Model
16
a
In
de
x
In
de
x

Chapter 6 Verification Problems
6-12
COSMOSFFE Thermal
TYPE:
Steady-state heat conduction due to internal heat generation, PLANE2D elements.
REFERENCE:
J. N. Reddy, “An Introduction to the Finite Element Method.” McGraw-Hill Book
Co., 1984, p. 260.
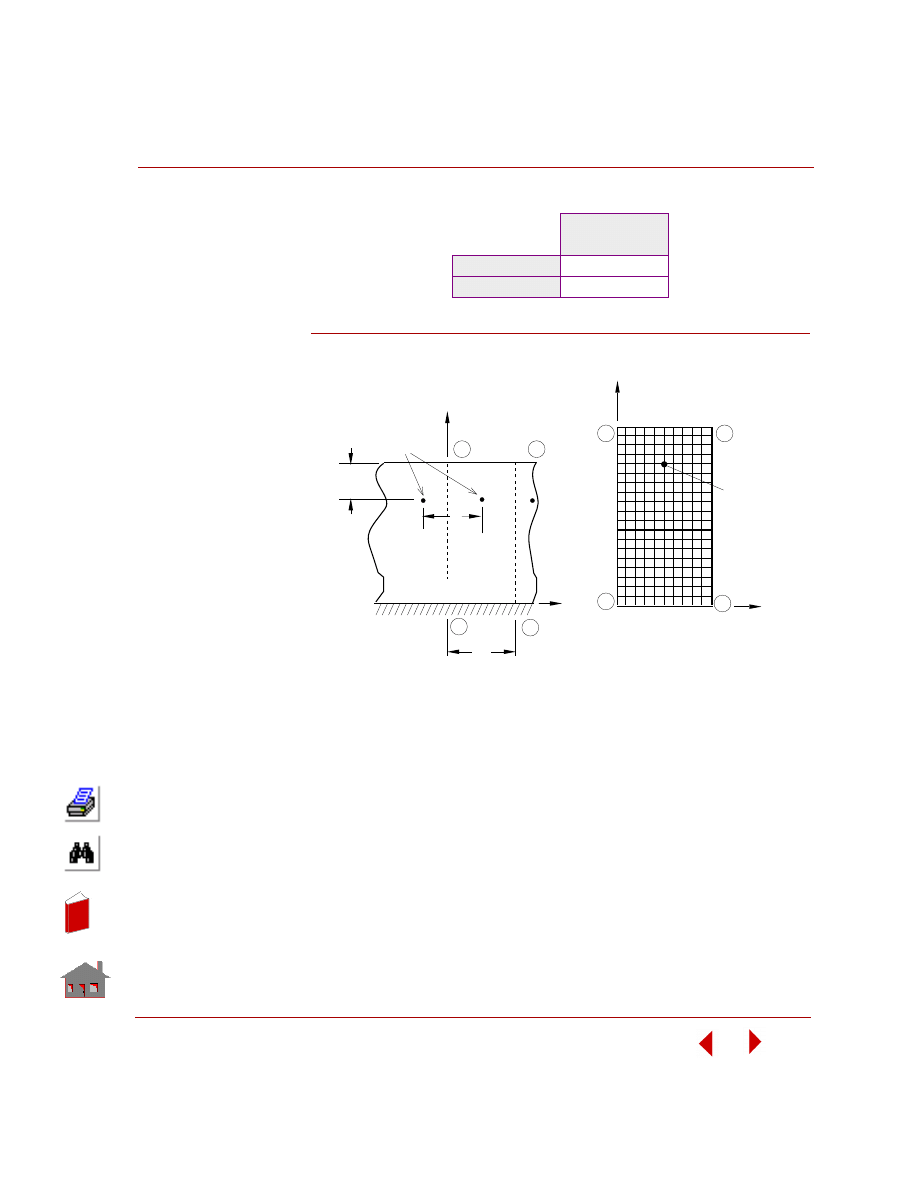
PROBLEM:
A series of heating cables have been placed in a conducting medium as shown in
figure. The medium has conductivities of K
x
=10 W/cm
°K and K
y
=15 W/cm
°K.
The upper surface is exposed to a temperature of -5
° C, and the lower surface is
bounded by an insulating medium. Assuming that each cable is a point source of 250
W, determine the temperature distribution in the medium.
GIVEN:
Thermal conductivity in x direction K
x
= 10 W/cm
°K
Thermal conductivity in y direction K
y
= 15 W/cm
°K
Ambient temperature T = 268
° K
Convection coefficient h = 5 W/cm
2
°K
Rate of heat generation in the cable
per unit length Q = 250 W
MODELING HINTS:
Since the cables are uniformly distributed throughout the medium, the problem can
be simplified by analyzing only the section ABCD as shown in the figure. Because
of symmetry, consider the sides AD and BC to be insulated. Since the medium is
symmetric about x-y plane, plane strain option of PLANE2D elements has been
selected.
FFETL05: Heat Conduction Due to a Series of
Heating Cables
In
de
x
In
de
x
COSMOSFFE Thermal
6-13
Chapter 6 Verification Problems
COMPARISON OF RESULTS:
Figure FFETL05–1.
Temperature
°
C
at node 113
Theory
----
COSMOSFFE
299.10
145
153
1
9
D
C
113
A
B
4
Cables
2
X
4
Y
T = 268
°
K
h = 5 w/cm
°
K
8
2
Insulated
Finite Element
Model
Y
X
Problem Sketch
Cabl
D
C
A
B
In
de
x
In
de
x

Chapter 6 Verification Problems
6-14
COSMOSFFE Thermal
TYPE:
Linear transient heat conduction, TRUSS2D elements.
REFERENCE:
Gupta, C. P., and Prakash, R., “Engineering Heat Transfer,” Nem Chand and Bros.,
India, 1979, pp. 155-157.
PROBLEM:
A large plate of thickness 62.8 cm is initially at a
temperature of 50
° C. Suddenly, both of its faces are
raised to and held at 550
° C.
Determine:
1.
The temperature at a plane 15.7 cm from the left
surface, 5 hours after the sudden change in
surface temperature.
2.
Instantaneous heat flow rate at the left surface at
the end of 5 hours.
3.
Total heat flow across the surface at the end of 5
hours.
GIVEN:
Thickness of slab = L = 0.628 m
Area of cross section = 1 m
2
Thermal Conductivity = K = 46.4 J/m - hr
°K
Density =
ρ = 23.2 Kg/m
3
Specific Heat = c = 1000 J/Kg -
°K
Initial Temperature = T
i
= 50
° C
Left and right
surface temperatures = T
s
= 550
° C
Solution Time = 5 hours
FFETL08:
Transient Heat Conduction in a Slab of
Constant Thickness
X
L
y
Problem Sketch
Ts
Ts
In
de
x
In
de
x

COSMOSFFE Thermal
6-15
Chapter 6 Verification Problems
MODELING HINT:
Since the other
dimensions of
plate are
infinitely large,
conduction
occurs through
thickness, i.e.,
along x-axis.
Therefore, this
problem can be
modeled with one
dimensional
elements having a
total length of (L
= 0.628 m) and
considering a
cross sectional area of (A = 1 m
2
). Sixteen TRUSS2D elements will be used to model
this problem as shown in Figure TL08-2.
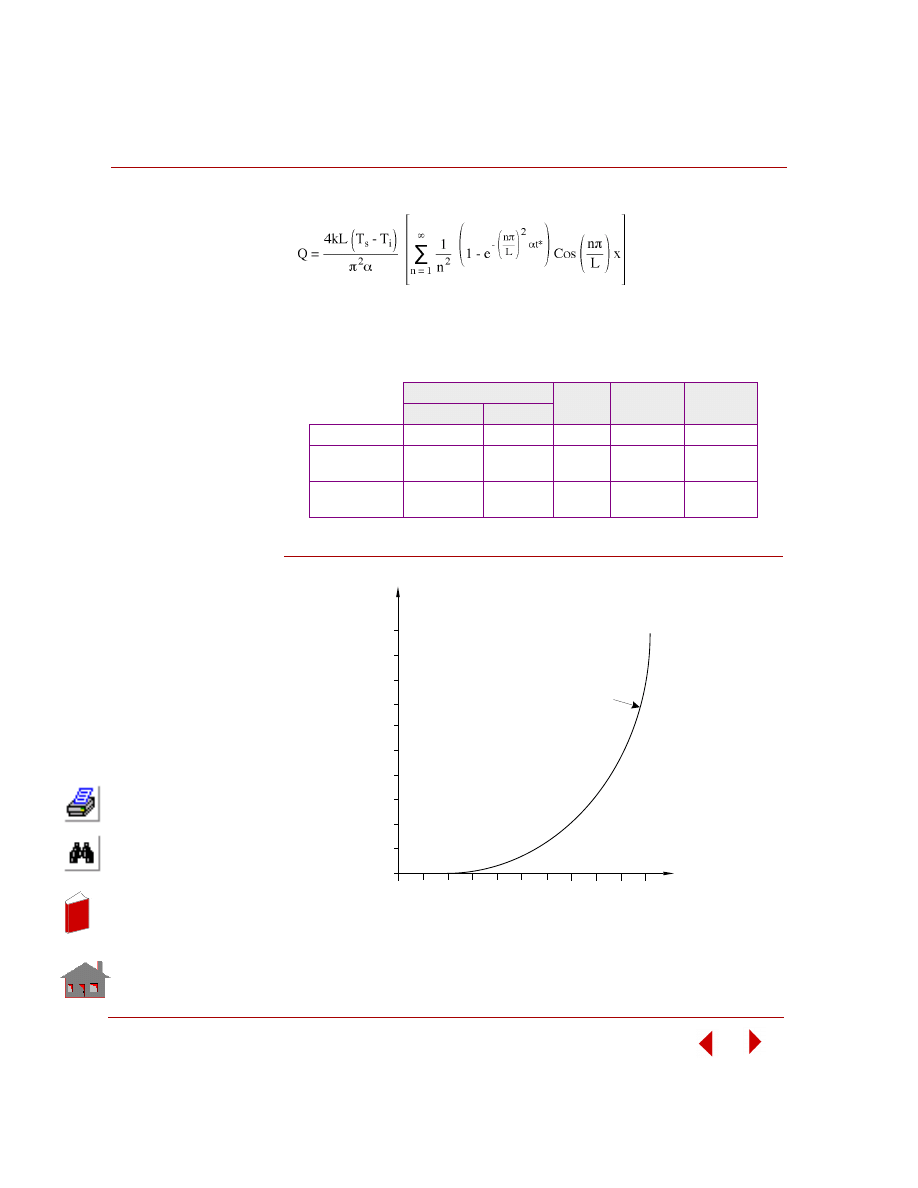
ANALYTICAL SOLUTION:
Let:
T
= Temperature at any point x
T
s
= Surface temperature
T
i
= Initial temperature
t
= Time
Temperature is:
(n = 1, 3, 5, ----)
Instantaneous heat flow rate per unit area at any point is:
(n = 1, 3, 5, ----)
Figure FFETL08-2.
L
1
2
3
4
17
16
15
14
1
2
3
14 15 16
X
Finite Element Model
0.0
5.0
1.0
Time
Te
m
p
.
0.0
Time. Temp. Curve
In
de
x
In
de
x
Chapter 6 Verification Problems
6-16
COSMOSFFE Thermal
Total heat flow during time t = 0 to t* is:
(n = 1, 3, 5, ----)
COMPARISON OF RESULTS:
At time t* = 5 hours:
Figure FFETL08–3.
Location
Theory
COSMOS
FFE
Difference
%
Distance (m)
Node No.
Temp (T)
0.157
5
183.90
183.42
0.05
Heat Flow/
Unit Time (q)
0
1
130880
130030
0.65
Cumulative
Heat Flow (Q)
0
1
1125330
1092200
2.94
78.6001
2.5250
0.0500
Time
64.3000
50.000
5.0000
Temperature Versus
Time for Node 9
Temperature
In
de
x
In
de
x
COSMOSFFE Thermal
6-17
Chapter 6 Verification Problems
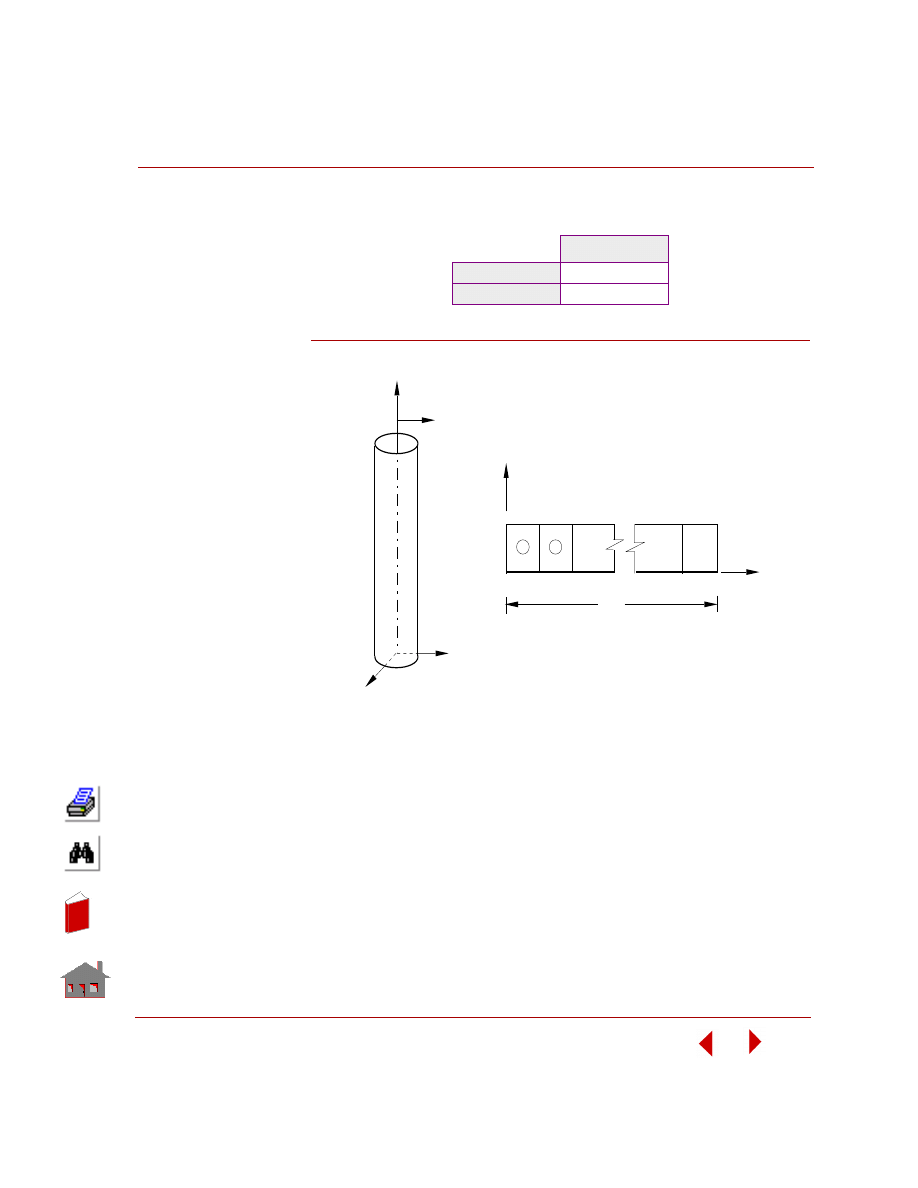
TYPE:
Heat transfer analysis, truss
elements and convection
link elements (CLINK).
REFERENCE:
Kreith, F., “Principles of
Heat Transfer”,
International Textbook Co.,
Scranton, Pennsylvania,
2nd Printing, 1959.
PROBLEM:
A cooling fin of square
cross-sectional area A,
length l, and conductivity k
extends from a wall
maintained at temperature
T
w
. The surface convection
coefficient between the fin
and the surrounding air is h,
the air temperature is T
a
,
and the tip of the fin is
insulated. Determine the
heat conducted by the fin q
and the temperature of the
tip T
l
.
GIVEN:
b
= 1 in = (1/12)ft
Area of Cross-Section
of the Fin
= A = 0.0069 ft
2
Length of Fin
= l = 0.667 ft
FFETL09: Heat Transfer from Cooling Fin
Figure FFETL09-1.
Y
X
Z
1
3
5
Y
h, T
b
T
b
l
w
a
Z
1
11
12
13
18
17
16
15
9
8
7
6
5
4
3
2
14
19
7
9
11
13
15
17
16
14
12
10
8
6
4
2
In
de
x
In
de
x
Chapter 6 Verification Problems
6-18
COSMOSFFE Thermal
Thermal Conductivity = k = 25 BTU/hr-ft-
°F
Film Coefficient
= h = 1 BTU/hr-ft
2
-
°F
Wall Temperature
= T
w
= 100
° F
Ambient Temperature = T
a
= 0
° F
CALCULATED INPUT:
The surface convection area per inch length of the fin = 0.02778 ft
2
.
MODELING HINTS:
The end convection elements are given half the surface area of the interior
convection elements. Nodes 11 through 19 are given arbitrary locations.
COMPARISON OF RESULTS:
T at node 9,
°
F
Theory
68.594
COSMOSFFE
68.615
Difference
0.03%
In
de
x
In
de
x

COSMOSFFE Thermal
6-19
Chapter 6 Verification Problems
TYPE:
Nonlinear heat conduction, TRUSS2D elements.
REFERENCE:
Ozisik, M., “Heat Conduction,” John Wiley and Sons Inc., 1980, pp. 440-443.
PROBLEM:
Determine the temperature distribution in a slab which is insulated on one face, and
subjected to a constant temperature on the other face. Assume constant internal heat
generation in the slab and a linear variation of thermal conductivity.
GIVEN:
Thickness of the slab
= L = 2 m
Internal heat generation = Q = 100,000 W/m
3
Thermal conductivity
= K = 50 (1 + 2T) W/m
° C
Boundary conditions:
At x = 0, Insulated boundary
At x = L, Prescribed temperature of 100
° C
Twenty TRUSS2D elements have been used to model this problem as shown in the
figure.
ANALYTICAL SOLUTION:
Steady state heat conduction equation is given by:
Where:
K =
K
0
(1+
β T), K
0
and
β are constants.
Q = Rate of internal heat generation.
FFETN01: Heat Conduction with Temperature
Dependent Conductivity
In
de
x
In
de
x
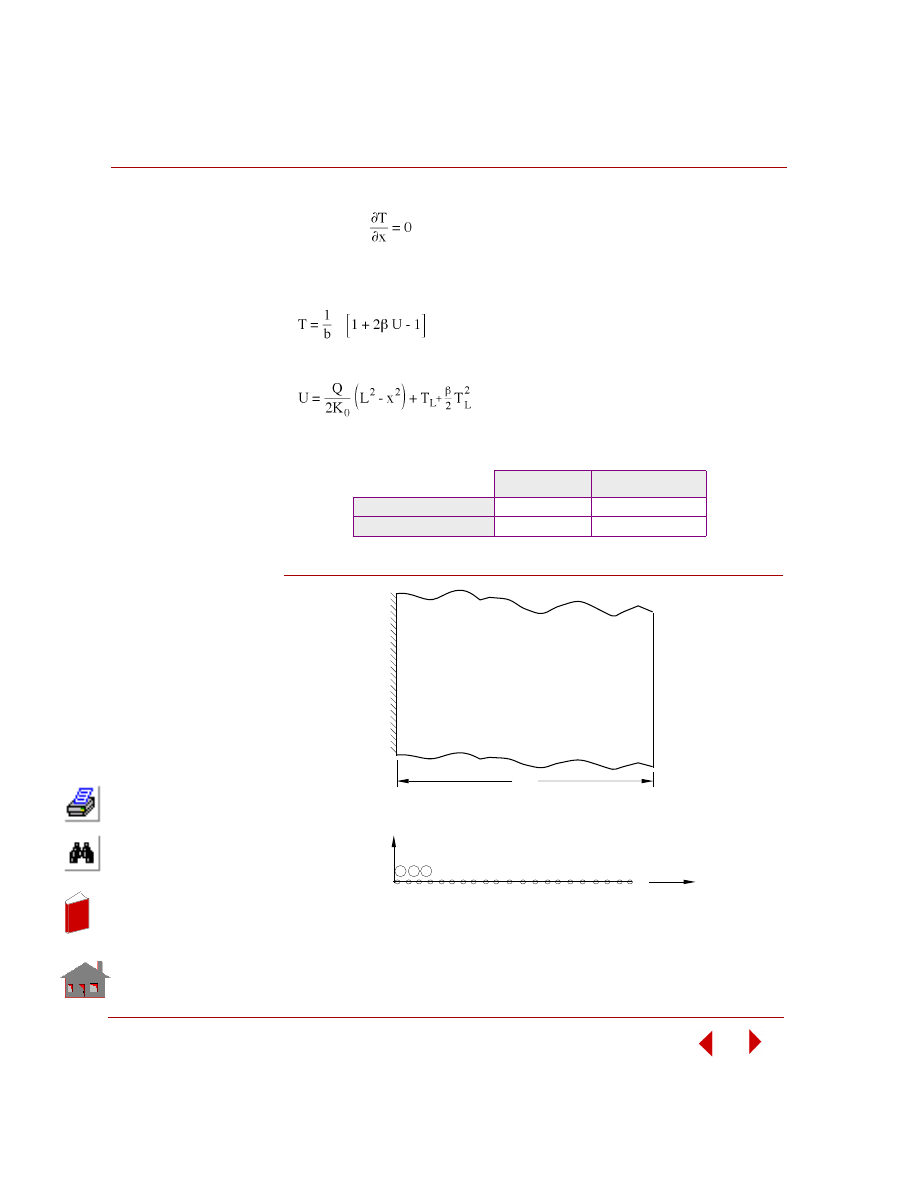
Chapter 6 Verification Problems
6-20
COSMOSFFE Thermal
Associated boundary conditions are:
At x = 0,
At x = L, T = T
L
(Prescribed temperature)
Solution of this problem can be obtained by Kirchoff transformation as:
Where:
COMPARISON OF RESULTS:
Figure FFETN01–1.
Theory
COSMOSFFE
At X = 0 (Node 1)
°
C
118.24
118.24
At X = 1 (Node 11)
°
C
113.96
113.96
Finite Element Model
Q = 100000.0 W/m
K = 50.0(1+2T) W/m C
T = 100.0 C
o
Insulated
20
L
Problem Sketch
1 2 3 4
20
1 2 3
21
Y
X
o
3
In
de
x
In
de
x

COSMOSFFE Thermal
6-21
Chapter 6 Verification Problems
TYPE:
Nonlinear steady-state analysis, TRUSS2D elements and radiation link (RLINK)
elements.
BOUNDARY CONDITIONS:
Prescribed temperatures at x = 0
Radiation at x = 10 m
PROBLEM:
Determine the temperature distribution in a rod in which the left end has a prescribed
temperature and the right end is radiating heat into the ambient atmosphere.
Figure FFETN03–1
GIVEN:
Length of the rod
= 10 m
Area of cross section
= 1 m
2
Thermal conductivity
= K = 45 W/m
°C
Ambient temperature
= T
∞
= 10
° C
Prescribed temp. at left end
= T
0
= 1000
° C
Radiation Data
Area of radiating surface
= 1 m
2
View factor
= 1
Emissivity
= 1
Stefan-Boltzmann constant
= 5.67E-8 W/m
2
°K
4
FFETN03: Radiation in a Rod
T=1000 C
T =10.0 C
Radiation
8
x
∞
∞
In
de
x
In
de
x

Chapter 6 Verification Problems
6-22
COSMOSFFE Thermal
Figure FFETN03–2
ANALYTICAL SOLUTION:
Figure FFETN03–3
Temperature distribution in a rod:
Boundary Conditions:
Temperature at
x = 0 T = T
0
Radiation at
x = l
Governing differential equation is:
d
2
T/dx
2
= 0
dT/dx
= C
1
T
= C
1
x + C
2
Applying boundary conditions at x = 0, T = T
0
, will result in C
2
= T
0
TRUSS 2D
Rlink
10
11
12
9
1
2
3
1
2
9
10
11
x=0
x=10
x
x
T
T
l
8
0
In
de
x
In
de
x

COSMOSFFE Thermal
6-23
Chapter 6 Verification Problems
Applying boundary conditions at x = l results in
But we have
Substitute:
σ = 5.67E-8 W/m
2
°K
4
ε
= 1
f
= 1
A
= 1 m
2
K
= 45 W/m
°K
T
0
= 1000
° C = 1273.15 °K
T
∞
= 10
° C = 283.15 °K
In
de
x
In
de
x

Chapter 6 Verification Problems
6-24
COSMOSFFE Thermal
Solution of the nonlinear algebraic equation, using the Newton-Raphson method:
Let the internal heat generation Q = 0
COMPARISON OF RESULTS:
Var.
x
y
z
Node
Analytical
COSMOSM
Temp
10
--
--
11
235.77
235.77
In
de
x
In
de
x
COSMOSFFE Thermal
A-1
A
Troubleshooting
Introduction
When you use the COSMOSFFE Thermal module, you may sometimes come
across the following error messages, listed alphabetically. Diagnostics and
corrective measures for each error messages are provided.
PROBLEM:
Bonding is not supported
You have specified bonding of two bodies in your model using the
BONDDEF
command. Bonding is not supported in this version of FFE Thermal. Delete
bonding or use the conventional HSTAR module.
PROBLEM:
Cannot restart because previous results are not compatible
Some changes in the model were introduced after the results existing in the
database have been calculated. Use the
RESTART
(Analysis >
Restart
) com-
mand to deactivate the restart option and try again.
PROBLEM:
Cannot restart without previous results
You have activated the restart option for transient thermal analysis. Results of
the analysis were not found in the database. Use the
RESTART
(Analysis >
Restart
) command to deactivate the restart option and try again.
In
de
x
In
de
x

Appedix A Troubleshooting
A-2
COSMOSFFE Thermal
PROBLEM:
Cannot restart without results for the starting point
You have activated the restart option for transient thermal analysis. Results of
the analysis at the starting solution step were not found in the database.
PROBLEM:
Coordinate system <number> is referenced but not defined
Define the missing coordinate system and try again or modify your input such
that the named coordinate system is not referred to.
PROBLEM:
Degenerate element <number>
Degenerate elements were detected in your model. Degenerate elements are bar
elements with 0-length, area elements with 0-area, or solid elements with 0-vol-
ume. Use the
ECHECK
(Meshing > ELEMENTS >
Check Element
) command
to correct the problem and automatically delete bar elements whose length is
less than
PTTOL
, area elements whose area is less than
PTTOL
square, and solid
elements whose volume is less than
PTTOL
cubed. The point tolerance is
defined by the
PTTOL
(Geometry > POINTS >
Merge Tolerance
) command.
PROBLEM:
Element <number> has unsupported type
The given element is associated with an element group that is not supported in
this release of FFE Thermal. Use the conventional solver, or redefine the ele-
ment group if possible.
PROBLEM:
Element <number> is pyramid shaped, which is not supported
The named element belongs to a SOLID element group. The nodes defining a
face of the solid have collapsed to a single point. This type of collapsed element
is not currently supported by COSMOSFFE Thermal. This element may have
been defined manually or resulted from the parametric meshing of a volume
with a very sharp edges or corners. Delete the mesh, define a TETRA4, or
TETRA10 element group, and use automatic meshing instead of parametric
meshing. Prism-shaped elements are automatically supported.
PROBLEM:
Error while closing a temporary file
An I/O error occurred while closing a temporary file.
In
de
x
In
de
x

COSMOSFFE Thermal
A
-3
Chapter A Troubleshooting
PROBLEM:
Error while positioning a temporary file
An I/O error has occurred while reading information from a temporary working
file.
PROBLEM:
Error while reading file <filename>
An I/O error has occurred while reading from the named file which is part of the
COSMOSM database. The file may have been corrupted. Check the integrity of
your hard disk, reconstruct the model by creating a new problem and using the
FILE
(File >
Load...
) command, and try again.
PROBLEM:
Error while reading from a temporary file
An I/O error has occurred while reading information from a temporary working
file.
PROBLEM:
Error while writing to a temporary file
An error occurred while writing data to the temporary file. Check the available
disk space, and the integrity of your system, especially the hard disk. Recon-
struct the database and try again.
PROBLEM:
Error while writing to file <filename>
An error occurred while writing data to the named file. Check the integrity of
your system, especially the hard disk. Reconstruct the database and try again.
PROBLEM:
File <filename> does not contain necessary data
The named file does not contain the expected data in the expected format. Either
the file is corrupted, overwritten, or created by a different COSMOSM version.
PROBLEM:
File <filename> has invalid format
The format of the data in the named file is not as expected. Either the file is cor-
rupted, overwritten, or created by a different COSMOSM version.
PROBLEM:
Improper
axisymmetric
model
The defined axisymmetric model is improper. Axisymmetric elements must be
defined in the global X-Y plane with the Y-axis as the axis of symmetry.
In
de
x
In
de
x

Appedix A Troubleshooting
A-4
COSMOSFFE Thermal
PROBLEM:
Improper mesh near element <number>
The mesh elements are not compatible in the neighborhood of the named ele-
ment. This can be the result of improper node merging, invalid parametric tetra-
hedral mesh, or invalid manually created elements.
PROBLEM:
Improper mesh, properties, or boundary conditions
Either the mesh, material properties, or boundary conditions of the model have
been improperly defined. Use the
R_CHECK
(Analysis >
Run Check
) com-
mand to check the elements. Also list and examine the material properties and
boundary conditions.
PROBLEM:
Incompatible
element groups
The generated mesh connects elements with incompatible element groups to
each other. Try to use other alternatives such that connected elements have com-
patible degrees of freedom.
PROBLEM:
Internal error # <number>
An internal error has occurred. Record the error number and report to SRAC.
PROBLEM:
Invalid combination of first and second order elements
First order (linear) and second order (parabolic) elements are connected to each
other resulting in incompatible common edges. An example is connecting
TETRA4 elements to TETRA10 elements. Use the
ECHANGE
(Meshing >
Element Order
) command to fix the problem by raising the order of first order
elements or lowering the order of second order elements. It is recommended,
though not necessary to change the element group(s).
PROBLEM:
Invalid curve
An invalid temperature or time curve has been found. Verify your input. The
ACTXYPRE
(Display XY PLOTS >
Activate Pre-Proc
) and
XYPLOT
(Display
XY PLOTS >
Plot Curves
) commands may be used to plot time and tempera-
ture curves. Redefine the invalid curves using the
CURDEF
(LoadsBC > FUNC-
TION CURVE >
Time/Temp Curve
) command and try again. A corruption in the
database is possible.
In
de
x
In
de
x

COSMOSFFE Thermal
A
-5
Chapter A Troubleshooting
PROBLEM:
Invalid order of nodes for element <number>
The number of nodes used to define the specified element is invalid. Use the
(Edit > LIST >
Element Groups
) and
ELIST
(Edit > LIST >
Elements
) com-
mands to find the error. The
R_CHECK
(Analysis >
Run Check
) command will
also detect such errors.
PROBLEM:
Invalid time interval for the analysis <start>, <end>
The time interval specified for the transient thermal analysis is invalid. Use the
TIMES
(LoadsBC > LOAD OPTIONS >
Time Parameter
) command to correct
the error.
PROBLEM:
Maximum number of nonlinear iterations <number> exceeded
The maximum allowable number of nonlinear iterations has been exceeded
without conversion. Check your input. Allow a higher number of iterations if no
errors are found. Use a smaller time interval for transient analysis.
PROBLEM:
Not enough boundary conditions
None or inadequate boundary conditions specified. Use commands in the
LoadsBC > HEAT TRANSFER menu to check your input. Specify more bound-
ary conditions and try again.
PROBLEM:
Out of memory or swap space
Available virtual memory is not sufficient to run this problem.
On UNIX systems contact your system administrator to increase size of the
swap space.
PROBLEM:
Too many time steps
The number of time steps for transient thermal analysis exceeded the maximum
allowed number which is currently 2400.
PROBLEM:
Unable to create a temporary file
The program could not create a temporary file. Check the integrity of your sys-
tem and verify that adequate disk space is available.
In
de
x
In
de
x

Appedix A Troubleshooting
A-6
COSMOSFFE Thermal
PROBLEM:
Unable to create file <filename>
The program could not create the named file. Check the integrity of your system
and verify that adequate disk space is available.
PROBLEM:
Unable to open file <filename>
The program could not open the named file which is part of the COSMOSM
database. The file may have been deleted. Check the integrity of your hard disk,
reconstruct the model by creating a new problem and using the
FILE
(File >
Load...
) command.
PROBLEM:
Unable to open problem database
The program could not open the database for this problem. Verify that the data-
base files for this problem exist in the proper path and directory specified and
that the correct version is being used. Also check the integrity of your system
and verify that adequate disk space is available.
PROBLEM:
Unexpected end of file while reading <filename>
An end-file mark was found before reading all needed data from the named file.
Check related input, fix the problem if any, and try again. Regenerate the file if
possible, check the integrity of your system and reconstruct the database
through the
FILE
(File >
Load...
) command if the problem could not be fixed
otherwise.
PROBLEM:
You are not authorized to use this type of analysis
You are not authorized to use this type of analysis. Use the
PRODUCT_INFO
(Control > MISCELLANEOUS >
Product Info
) command to get a list of the
modules you are authorized to use. Contact S.R.A.C.
PROBLEM:
Zero or negative cross section area for element <number>
The cross sectional area of the specified element is zero or negative. Use the
ELIST
(Edit > LIST >
Elements
) command to find the associated real constant
set and then use the
RCLIST
(Edit > LIST >
Real Constants
) command to list
the cross sectional area. Use the
RCONST
(Propsets >
Real Constant
) com-
mand to specify a positive value.
In
de
x
In
de
x

COSMOSFFE Thermal
A
-7
Chapter A Troubleshooting
PROBLEM:
Zero or negative heat conductivity for element <number>
The heat conductivity specified for this element is zero or negative. Use the
ELIST
(Edit > LIST >
Elements
) command to find the associated material prop-
erty set and then use the
MPLIST
(Edit > LIST >
Material Props
) command to
list the material properties in the associated set. Use the
MPROP
(Propsets >
Material Property
) command to specify a positive value.
PROBLEM:
Zero or negative real constant for radiation link element <number>
An invalid value has been specified in the real constant associated with the spec-
ified element. Use the
ELIST
(Edit > LIST >
Elements
) command to find the
associated real constant set and then use the
RCLIST
(Edit > LIST >
Real Con-
stants
) command to list the set and check your input for the radiating surface
area, the view factor, emissivity, and the Stefan-Boltzman constant. Use the
RCONST
(Propsets >
Real Constant
) command to fix the error.
PROBLEM:
Zero or negative thickness for element <number>
The thickness of the specified element is zero or negative. Use the
ELIST
(Edit >
LIST >
Elements
) command to find the associated real constant set and then
use the
RCLIST
(Edit > LIST >
Real Constants
) command to list the thickness.
Use the
RCONST
(Propsets >
Real Constant
) command to specify a positive
value.
PROBLEM:
Zero or negative time increment
The time increment specified by the
TIMES
command is invalid. Use the
TIMES
(LoadsBC > LOAD OPTIONS >
Time Parameter
) command to specify a posi-
tive value.
In
de
x
In
de
x

A-8
COSMOSFFE Thermal
In
de
x
In
de
x

COSMOSFFE Thermal
I-1
Index
A
Activate Post-Proc 4-6
B
beam element 3-1
BEAM2D 3-1
BEAM3D 3-1
boundary condition 1-1
C
change element A-4
Change El-Prop 3-2
check element A-2
CLINK 3-1, 6-2
convection 1-2, 5-18, 6-5, 6-8
convergence tolerance 4-6
D
Data Check 4-7
Default Meshing 5-11
delete mesh 5-7
delete polyhedron 5-9
E
Element Group 3-2
element library 3-1
error messages A-1
F
FFE Static Options 4-5
FFE Thermal Options 4-5, 5-1
first order 4-6
H
heat flux 1-2
L
linear 5-1
list element groups A-5
M
mass matrix 4-6
material properties A-4, A-7
N
New Property Set 3-2
nonlinear 5-1, 5-10
O
Offset Temperature 5-13
P
postprocessing 4-2
preprocessing 4-2
Product Info A-6
Property Set 3-2
R
radiation 1-3
Read Temp as Load 4-5
RLINK 3-1, 6-2
Run Check A-5
Run Static Analysis 4-5
Run Thermal Analysis 4-6
S
second order 4-6
Set Entity 4-4
SHELL3 3-1
SHELL3T 3-1, 6-2
SHELL4 3-1, 6-2
SHELL4T 3-1
size limitations 2-3
SOLID 3-1
steady-state 4-5
Stefan-Boltzmann Constant 5-13
surfaces 5-3
In
de
x
In
de
x

Index
I-2
COSMOSFFE Thermal
T
temperature 1-2
TETRA10 3-2
TETRA4 3-2
Thermal Analysis Options 4-5
thermal stress 4-5
Time/Temp Curve 4-4, A-4
transient 4-5, 4-6
TRIANG 3-2
TRUSS 6-2
TRUSS2D 3-2, 6-2
TRUSS3D 3-2
U
units 1-3
In
de
x
In
de
x
Document Outline
- COSMOSFFE Thermal Analysis Module
- 1 Introduction
- 2 Capabilities
- 3 Element Library
- 4 Input Data
- 5 Examples
- 6 Verification Problems
- A Troubleshooting
- Index
Wyszukiwarka
Podobne podstrony:
Module ThermalAnalisys 2
Microwaves in organic synthesis Thermal and non thermal microwave
Module 10
Module 8
Food ćwiczenia angielski Starland 1 module 8
Instrukcja montażu sufitów podwieszanych w module 600x600mm System standardowy 600x600 1 AMF REINRAU
AT Commands for Bluetooth Module
Module 07
CISCO CCNA Certifications CCNA 2 Module 10
CISCO CCNA Certifications CCNA 2 Module 9
Module 12
CISCO CCNA Certifications CCNA 2 Module 1
delta module1 sample test01 1
06 BS Module 1 Section 6
CISCO CCNA Certifications CCNA 3 Module 3
53 755 765 Effect of Microstructural Homogenity on Mechanical and Thermal Fatique
Module 11
więcej podobnych podstron