Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie ślizgowe 

 

Rozpatrzmy tarczę o małej wysokości w porównaniu z długością.  
 
Tarcza spoczywa na powierzchni płaskiej.  
 
Powierzchnie styku tarczy i podłoża są szorstkie.  
 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie ślizgowe 

 

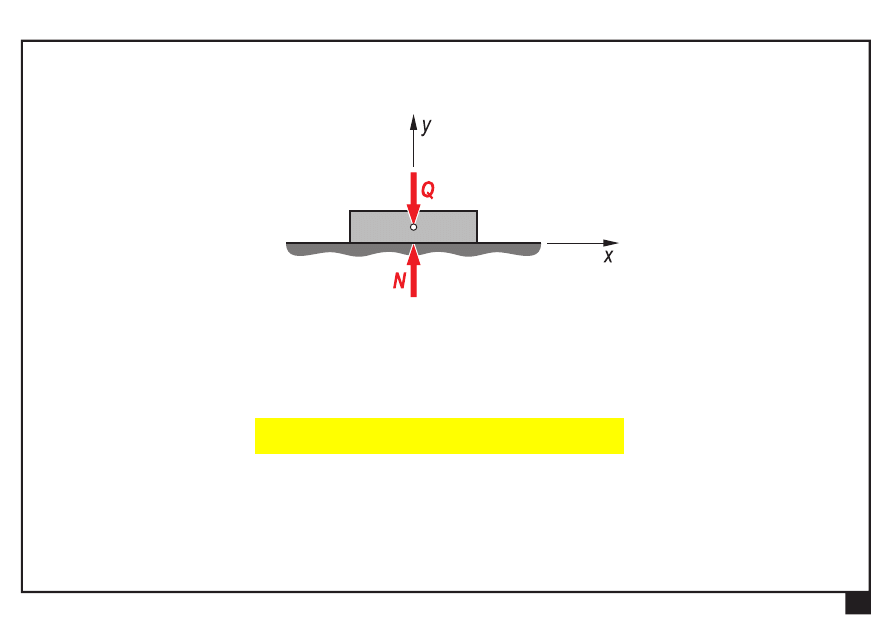
Układ sił (tarcza w spoczynku) 
Q — 

ciężar tarczy, 

g

m

Q 

  

N — 

nacisk 

podłoża na tarczę (reakcja podłoża) 

Q

N

N

Q

P

iy













0

:

0

Σ

 

 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie ślizgowe 

 

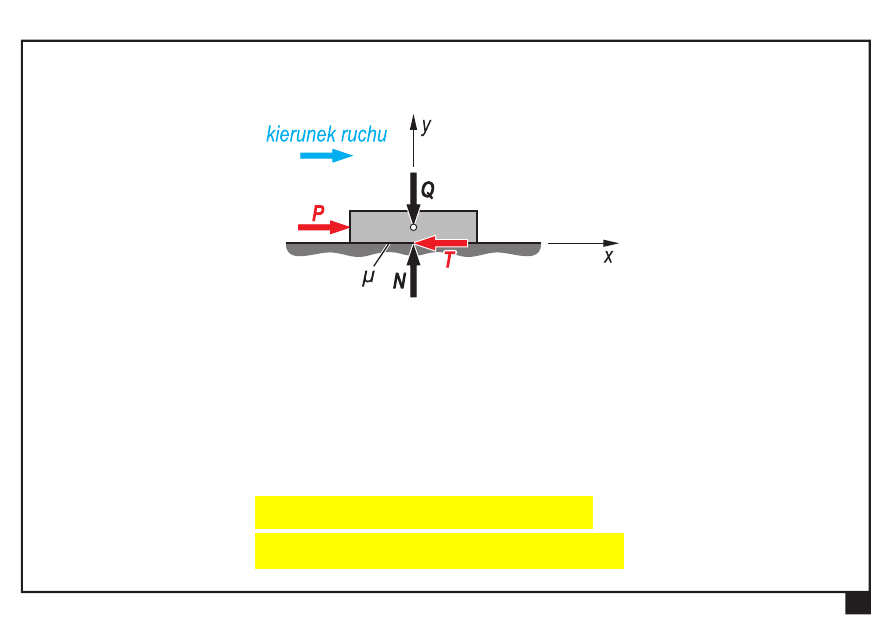
Układ sił (tarcza w ruchu) 
Q — 

ciężar tarczy, 

g

m

Q 

  

N — 

nacisk 

podłoża na tarczę (reakcja podłoża)  

P — 

siła pozioma przyłożona do tarczy  

T — 

siła tarcia ślizgowego 

T

P

T

P

P

ix











0

:

0

Σ

 

Q

N

N

Q

P

iy













0

:

0

Σ

 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie ślizgowe 

 

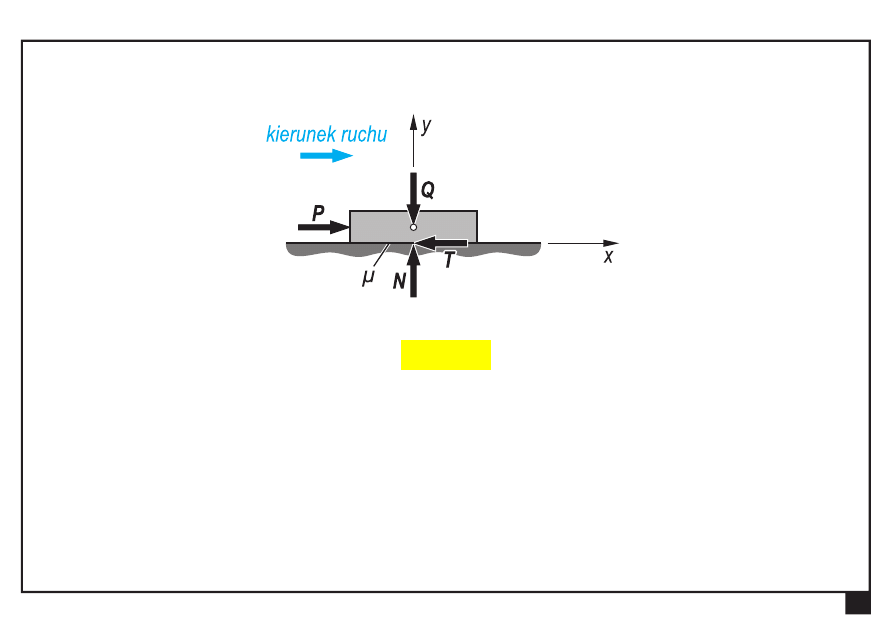
Prawo Coulomba (w warunkach równowagi granicznej)  

N

μ

T 

 

μ — 

współczynnik tarcia ślizgowego 

(statycznego rozwiniętego),

  

z zakresu 

1

0



 μ

 

N — 

nacisk 

podłoża na tarczę (wypadkowa) 

 

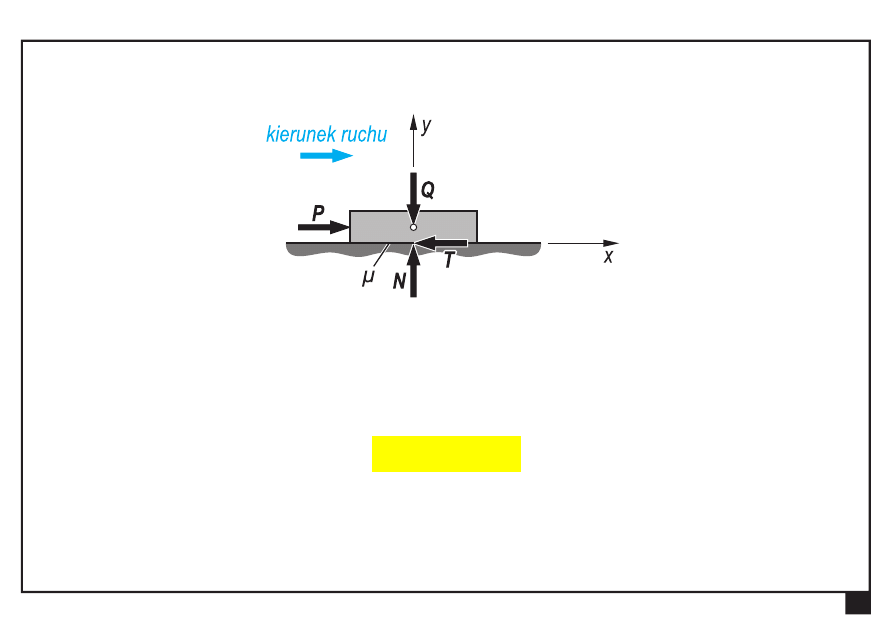
Siła tarcia T ma zwrot przeciwny do siły P  
(przeciwny do kierunku ruchu tarczy) 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie ślizgowe 

 

Po przekroczeniu równowagi granicznej następuje ruch ciała  
w kierunku działania siły P.  
 
Siłę przesuwającą 

gr

P

P 

 wyznaczamy w każdym zadaniu oddzielnie 

N

μ

T

P





gr

 

 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie ślizgowe 

 

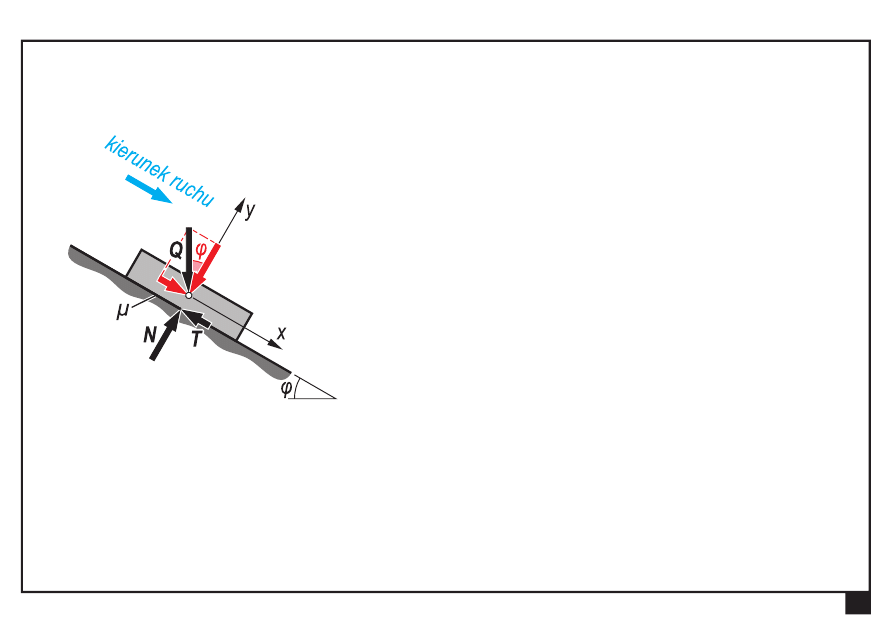
Rozpatrzmy tarczę spoczywającą  
na równi pochyłej.  
 
Przy pewnej wartości kąta φ   
tarcza zacznie się zsuwać. 
 

 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie ślizgowe 

 

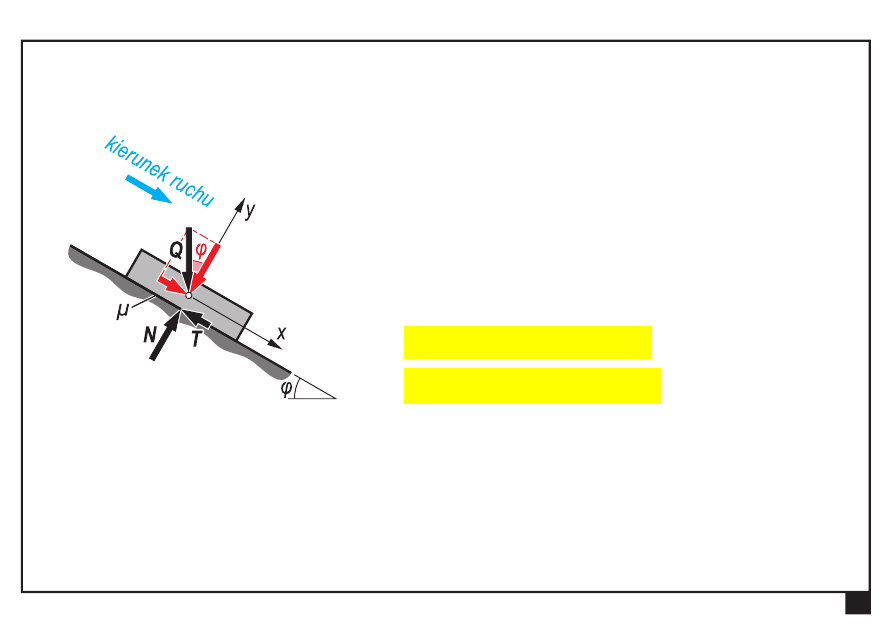
Rozpatrzmy tarczę spoczywającą  
na równi pochyłej.  
 
Przy pewnej wartości kąta φ   
tarcza zacznie się zsuwać. 
 
Warunki równowagi układu 

φ

Q

T

P

ix

sin

:

0

Σ





 

φ

Q

N

P

iy

cos

:

0

Σ





 

 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie ślizgowe 

 

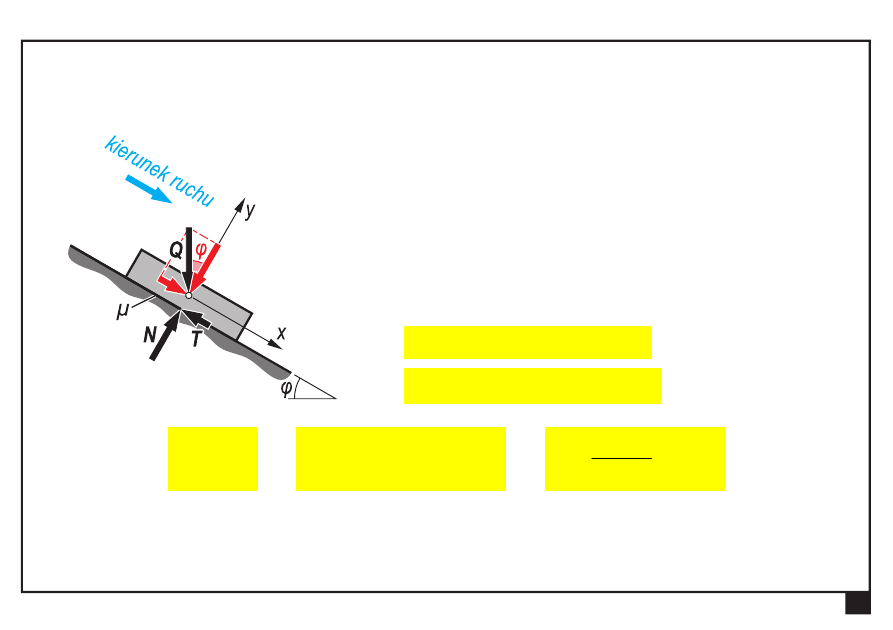
Rozpatrzmy tarczę spoczywającą  
na równi pochyłej.  
 
Przy pewnej wartości kąta φ   
tarcza zacznie się zsuwać. 
 
Warunki równowagi układu 

φ

Q

T

P

ix

sin

:

0

Σ





 

φ

Q

N

P

iy

cos

:

0

Σ





 

N

μ

T 

     

φ

Q

μ

φ

Q

cos

sin



     

φ

φ

φ

μ

tg

cos

sin





 

φ  — kąt tarcia, kąt nachylenia równi pochyłej, przy którym  

ciało (tarcza) zaczyna się zsuwać  

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie toczne (opór toczenia) 

 

Rozpatrzmy ciało sztywne typu walec, kula, baryłka.  
 
Model płaski — krążek o promieniu r.  
 

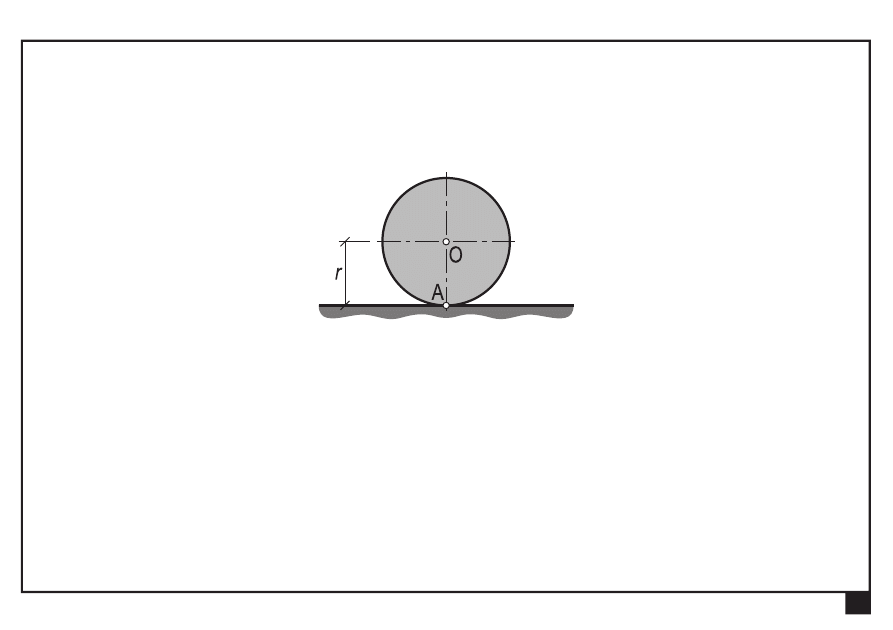
Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie toczne (opór toczenia) 

 

O — geometryczny 

środek krążka  

 
A  — teoretyczny punkt podparcia krążka (punkt styku z podłożem)  
 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie toczne (opór toczenia) 

 

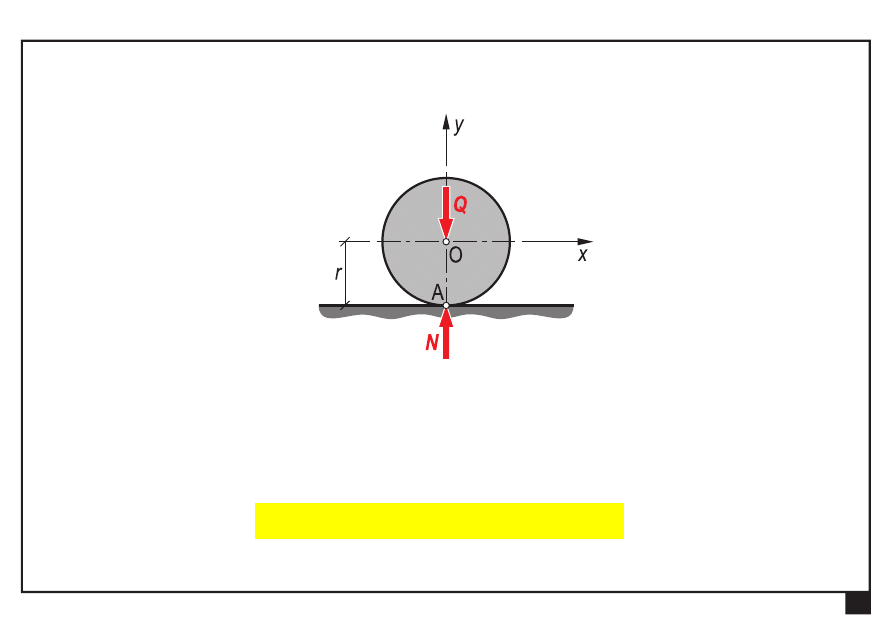
Układ sił (ciało w spoczynku) 
Q

 — 

ciężar tarczy, 

g

m

Q 

  

N

 — 

nacisk 

podłoża na krążek (reakcja podłoża) 

Q

N

N

Q

P

iy













0

:

0

Σ

 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

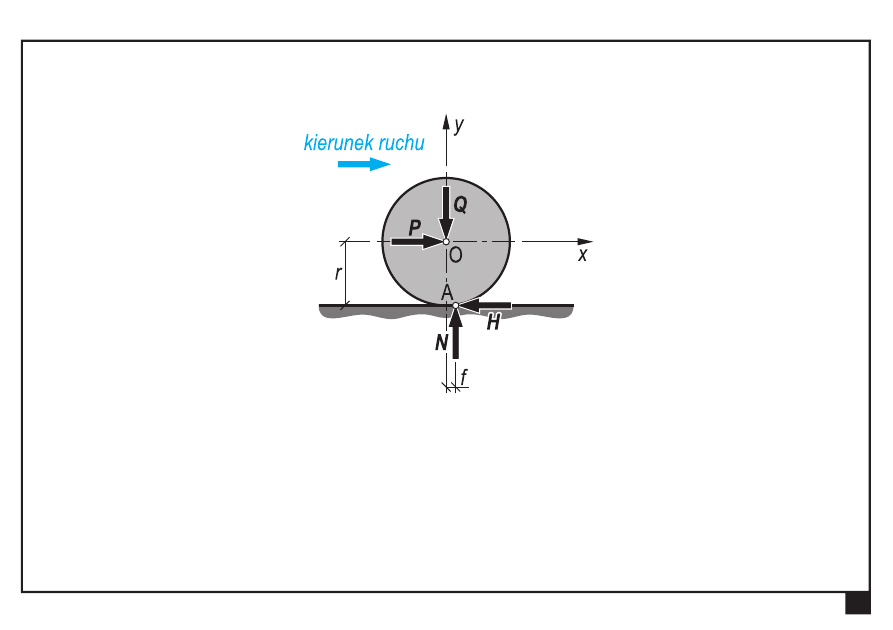
Tarcie toczne (opór toczenia) 

 

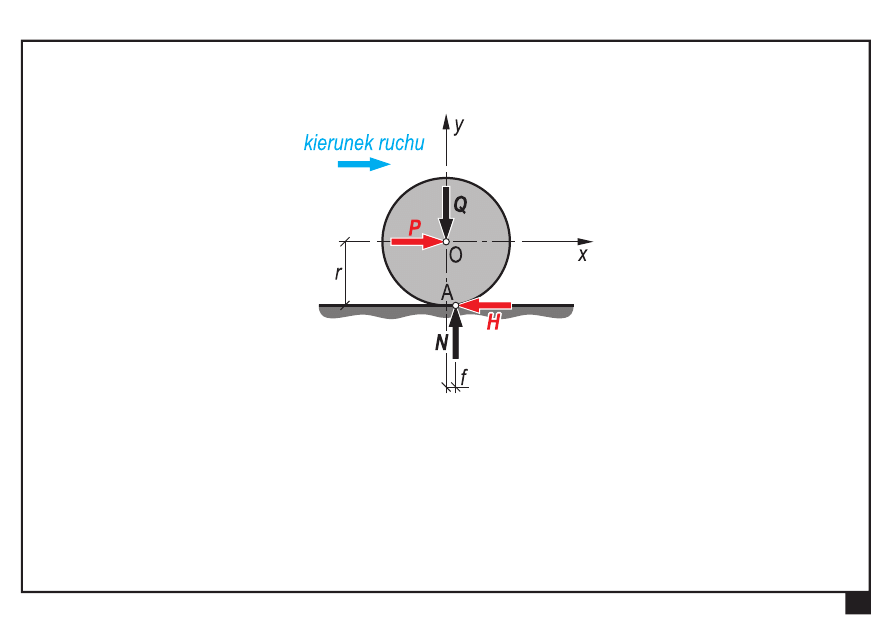
Przesunięcie teoretycznego punktu podparcia A w kierunku 
działania siły P o wielkość f 
 
Pochylenie reakcji podłoża (pojawienie się składowej poziomej H)  
 

f — 

współczynnik tarcia tocznego

 

(ramię oporu toczenia) [m]

 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

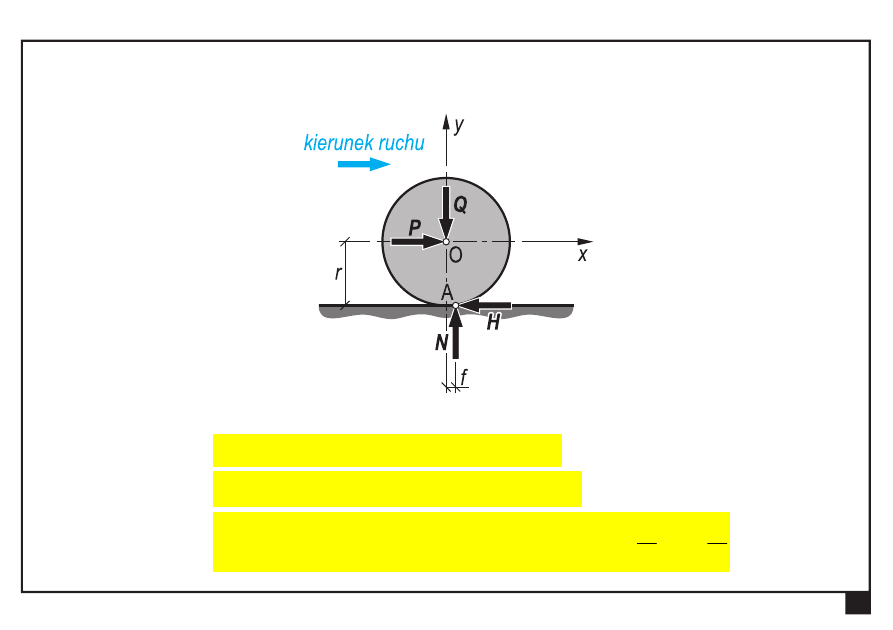
Tarcie toczne (opór toczenia) 

 

Układ sił (ciało w ruchu) 
Q

 — 

ciężar tarczy, 

g

m

Q 

  

N

 — 

nacisk 

podłoża na krążek (reakcja podłoża) 

P

 — 

siła pozioma przyłożona do krążka w punkcie O 

H

 — składowa pozioma reakcji podłoża 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

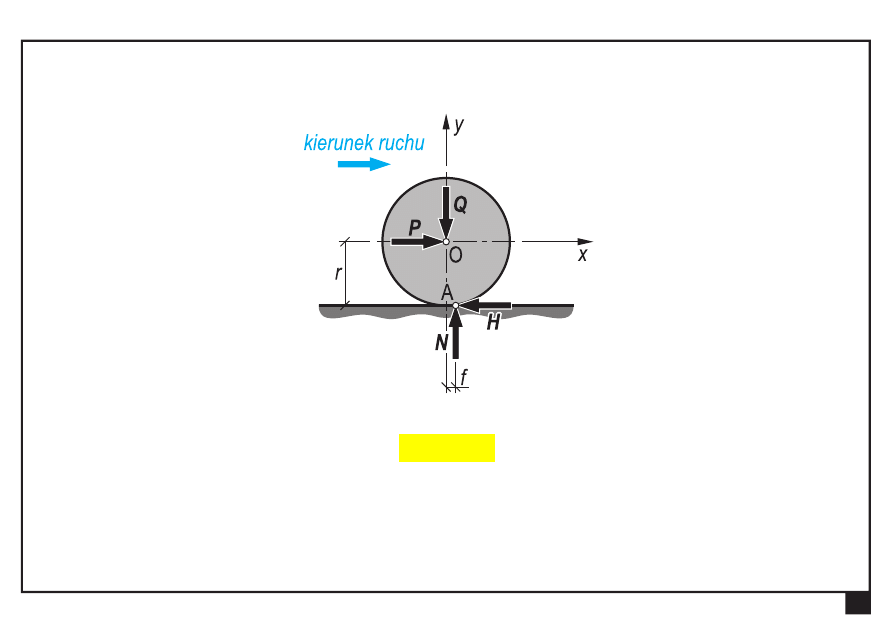
Tarcie toczne (opór toczenia) 

 

Układ sił (ciało w ruchu) 

P

H

H

P

P

ix











0

:

0

Σ

 

Q

N

N

Q

P

iy













0

:

0

Σ

 

r

f

Q

r

f

N

H

r

H

f

N

M

i

















0

:

0

Σ

O

 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

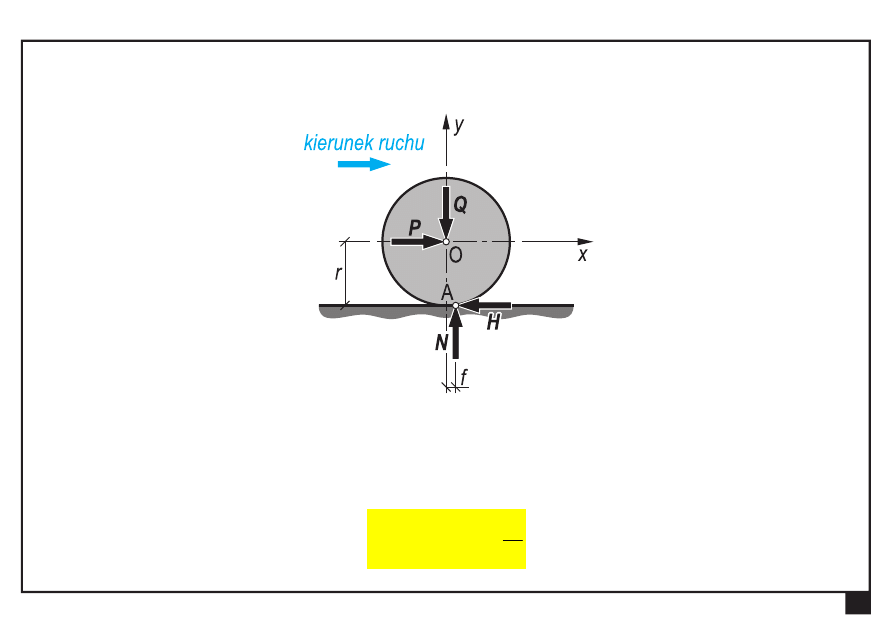
Tarcie toczne (opór toczenia) 

 

Warunek toczenia 

N

μ

H 

 

W przeciwnym przypadku nastąpi poślizg krążka 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie toczne (opór toczenia) 

 

Po przekroczeniu równowagi granicznej następuje toczenie się krążka  
w kierunku działania siły P. 
Siłę 

gr

P

P 

 wyznaczamy w każdym zadaniu oddzielnie 

r

f

N

H

P





gr

 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie cięgna o krążek (tarcie opasania)  

 

Rozważmy nieruchomy krążek. 
 

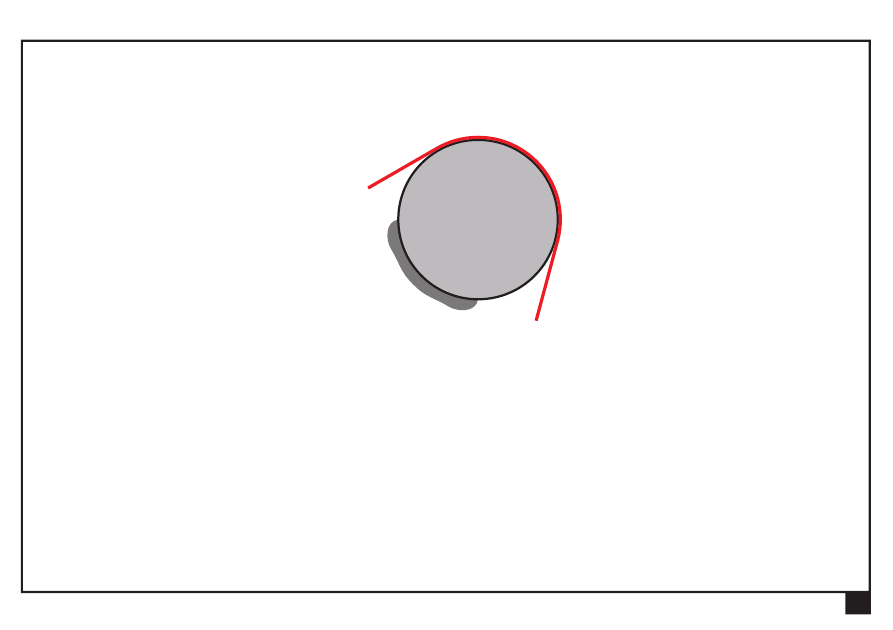
Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie cięgna o krążek (tarcie opasania)  

 

Przez krążek przełożono (lub owinięto) cięgno (pas, lina),  
element wiotki przenoszący 

tylko

 siłę rozciągającą 

— zakładamy, że cięgno jest 

nieodkształcalne

 

— cięgno przełożone przez krążek przyjmuje kształt krążka 
 

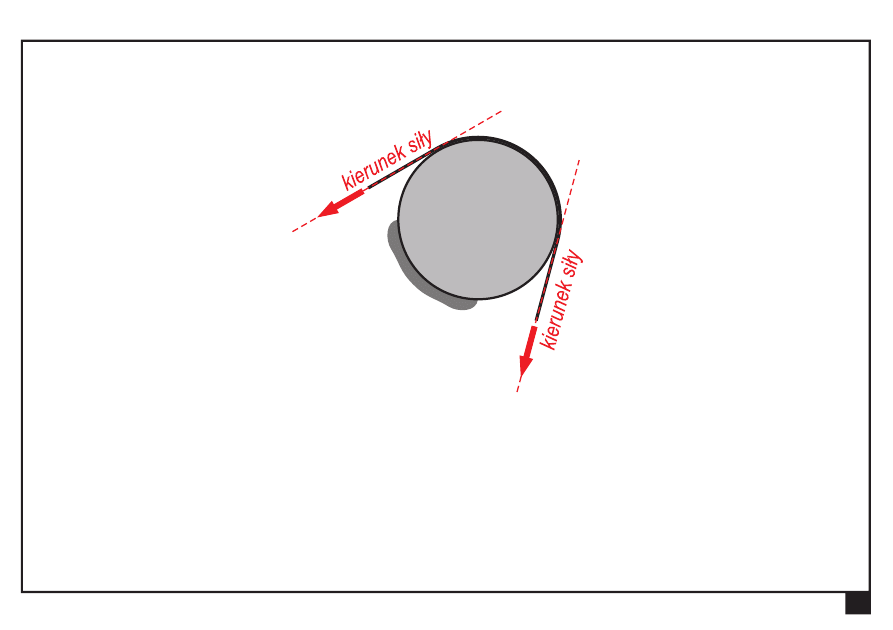
Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie cięgna o krążek (tarcie opasania)  

 

Przez krążek przełożono (lub owinięto) cięgno (pas, lina),  
element wiotki przenoszący 

tylko

 siłę rozciągającą 

— zakładamy, że cięgno jest 

nieodkształcalne

 

— cięgno przełożone przez krążek przyjmuje kształt krążka  
— krążek zmienia kierunek siły przenoszonej przez cięgno 

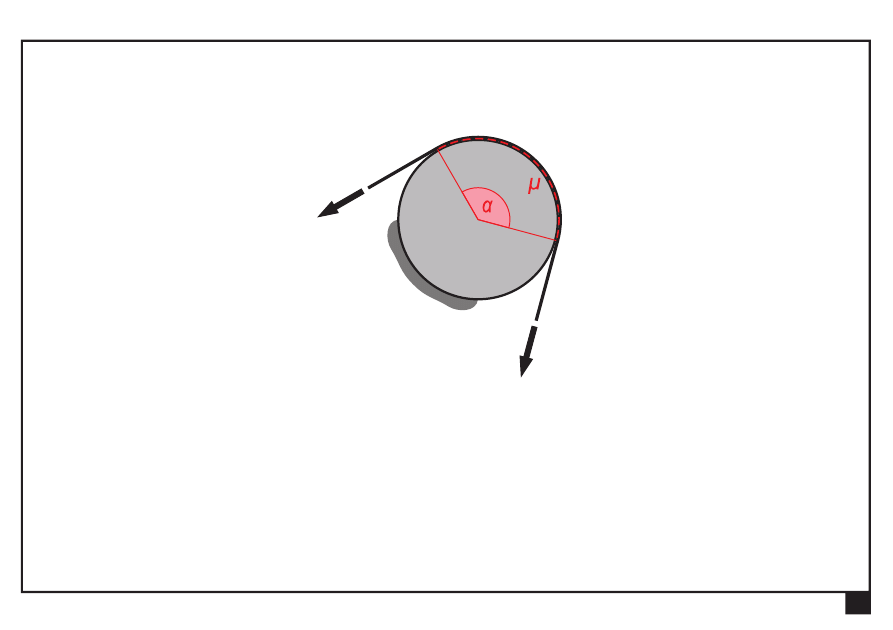
Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie cięgna o krążek (tarcie opasania)  

 

Pomiędzy cięgnem a powierzchnią krążka występuje tarcie  

μ  — współczynnik tarcia ślizgowego (rozwiniętego) cięgna o krążek 



 — kąt opasania [rad] 

 

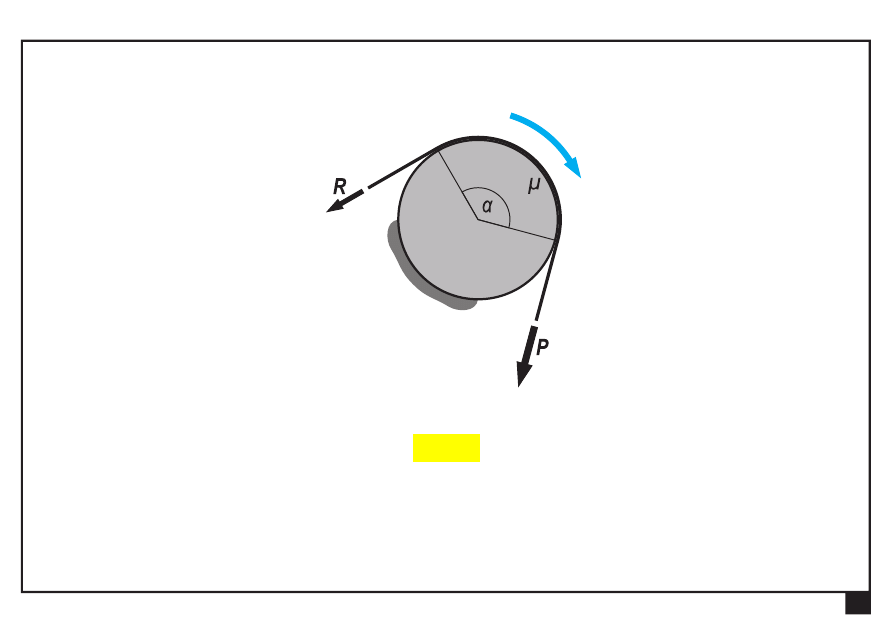
Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie cięgna o krążek (tarcie opasania)  

 

Naciągi lin po obu stronach krążka są 

różne

.  

R

P

  

siła bierna  siła czynna 

 

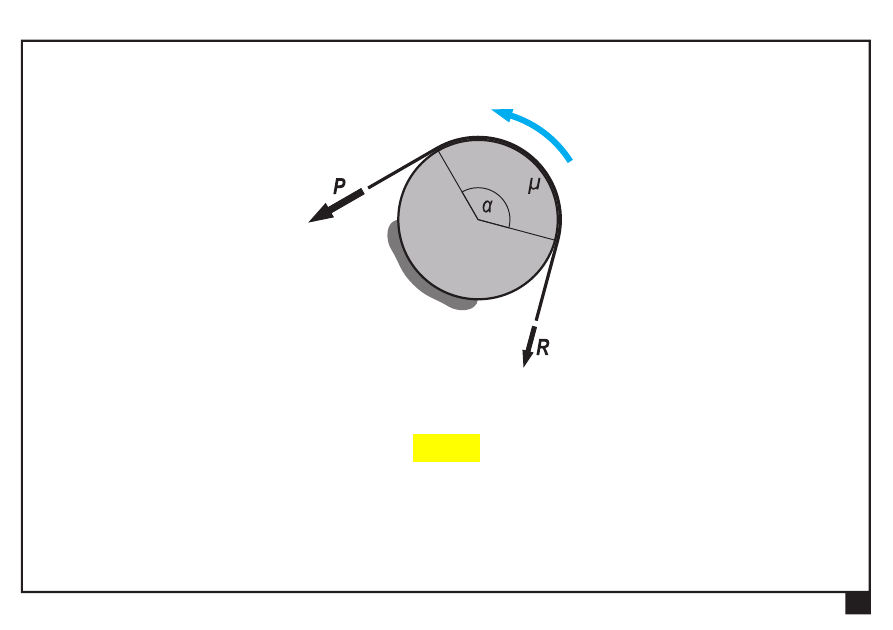
Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie cięgna o krążek (tarcie opasania)  

 

Naciągi lin po obu stronach krążka są 

różne

.  

R

P 

 

siła czynna  siła bierna 

 

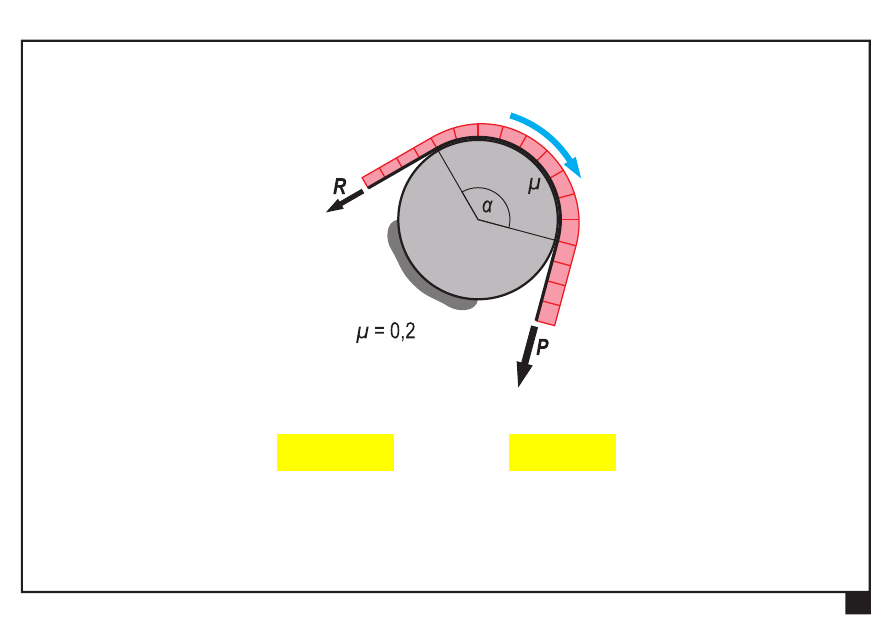
Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie cięgna o krążek (tarcie opasania)  

 

 



μ

P

R



 e

               

e

P

R





 

 

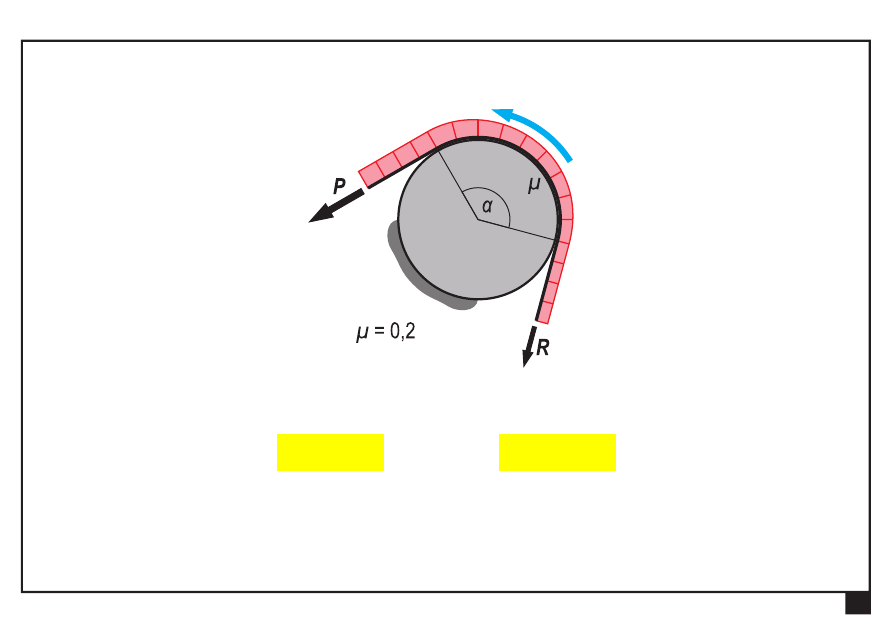
Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie cięgna o krążek (tarcie opasania)  

 

 

e

P

R





               

e

R

P







 

 

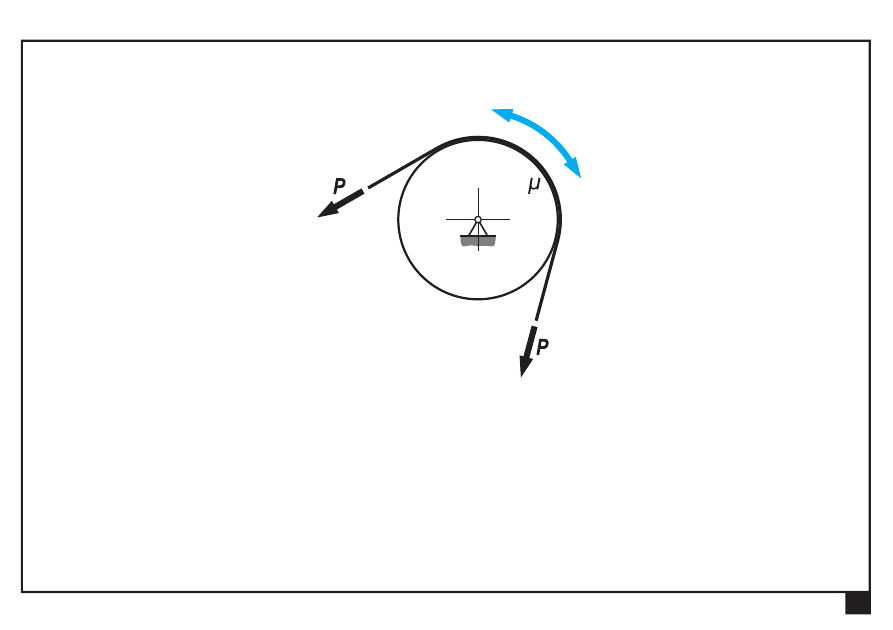
Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie cięgna o krążek (tarcie opasania)  

 

W przypadku cięgna przerzuconego przez krążek, który może się 
obracać, siły po obu stronach są 

jednakowe

.  

 

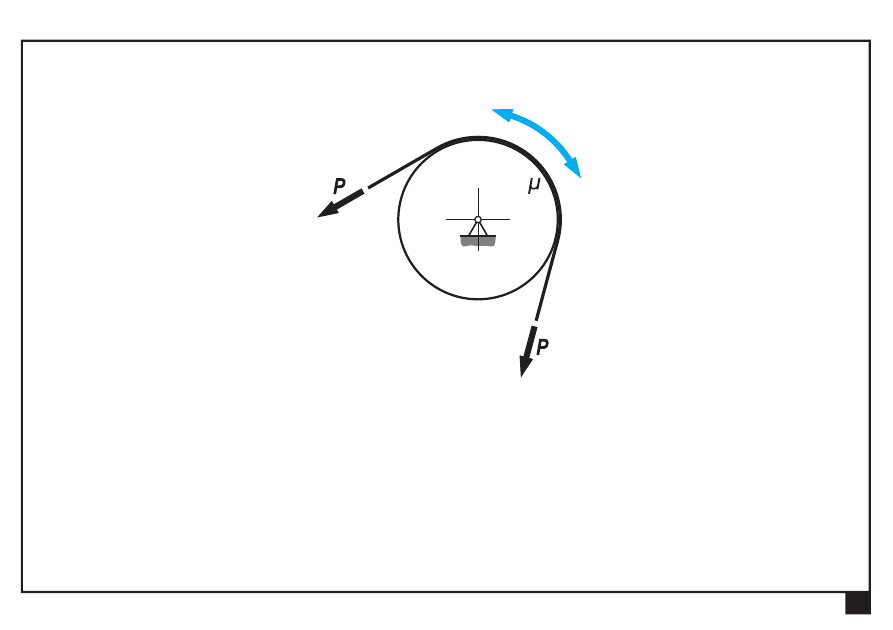
Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie cięgna o krążek (tarcie opasania)  

 

W przypadku cięgna przerzuconego przez krążek, który może się 
obracać, siły po obu stronach są 

jednakowe

.  

 
Krążek obraca się, dzięki sile tarcia wywiązującej się na styku  

cięgno – krążek

 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

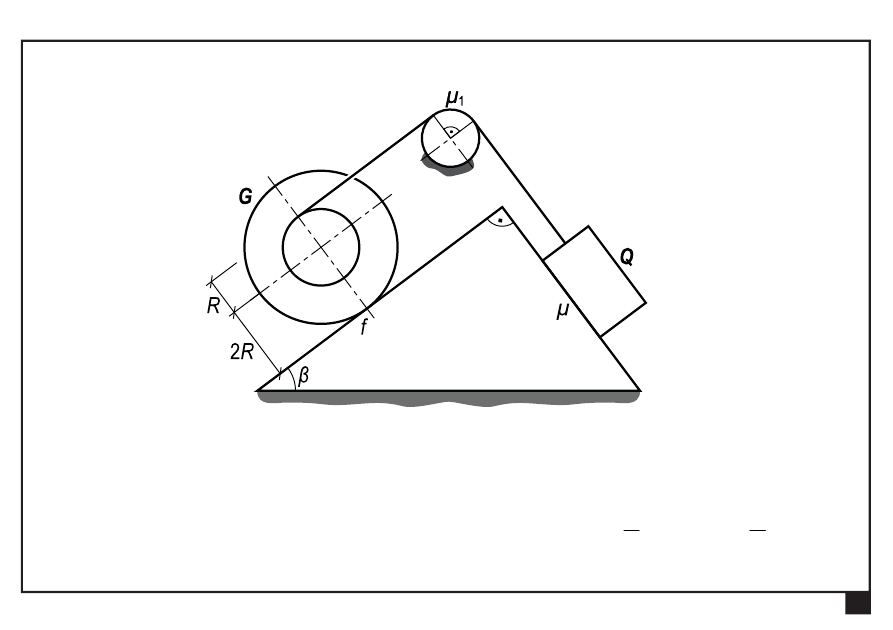
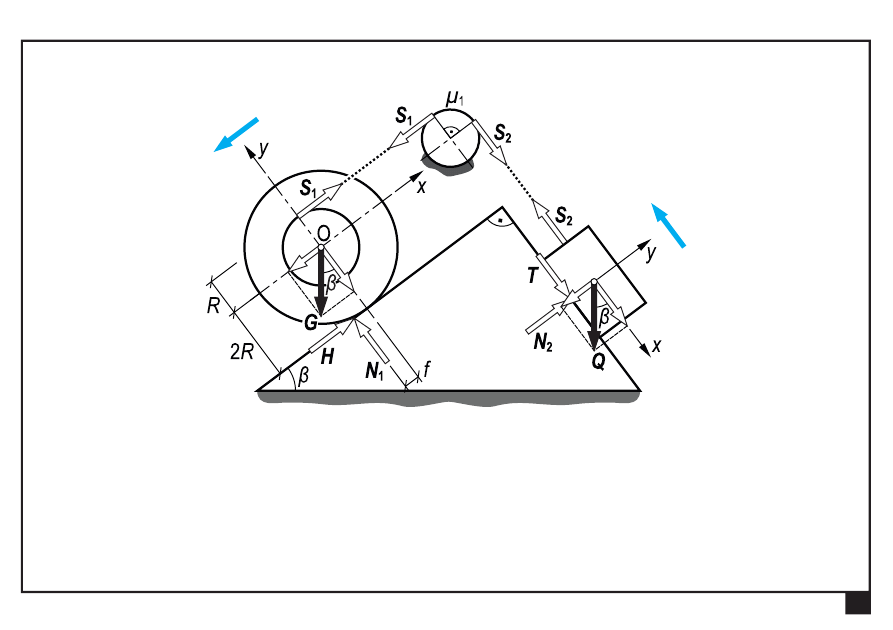
Tarcie — przykład  

 

 
Wyznaczyć wartości ciężaru krążka 

min

G

 i 

max

G

 w punktach 

równowagi granicznej.  

Dane: 

Q

, 

R

, 

R

f

05

,

0



, 

5

,

0



μ

, 

2

,

0

1



μ

, 

5

3

sin



β

, 

5

4

cos



β

 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie — przykład  

 

 
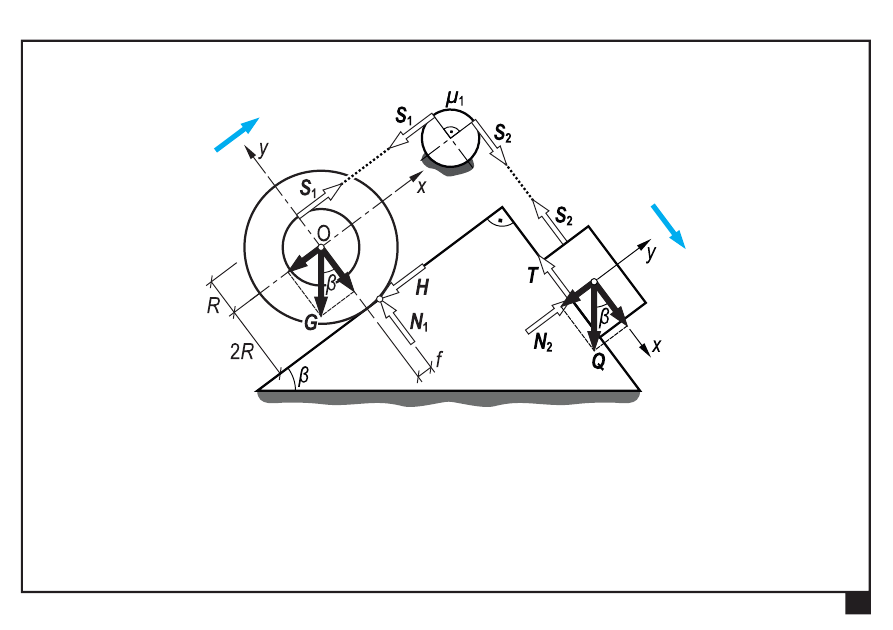
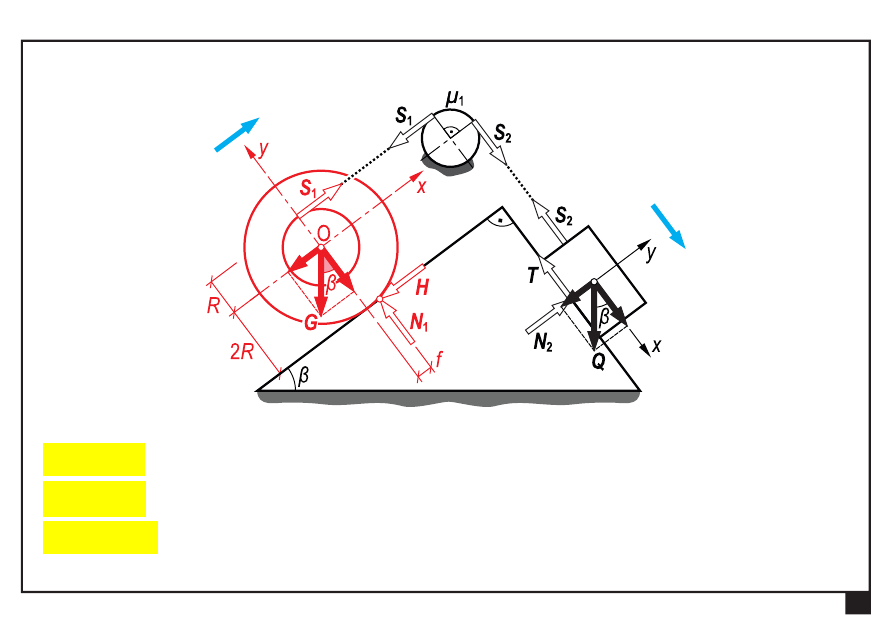
Wyznaczmy graniczną wartości ciężaru krążka 

min

G

.  

Bloczek o ciężarze Q zsuwa się w dół, natomiast krążek  
porusza się do góry 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie — przykład  

 

 

:

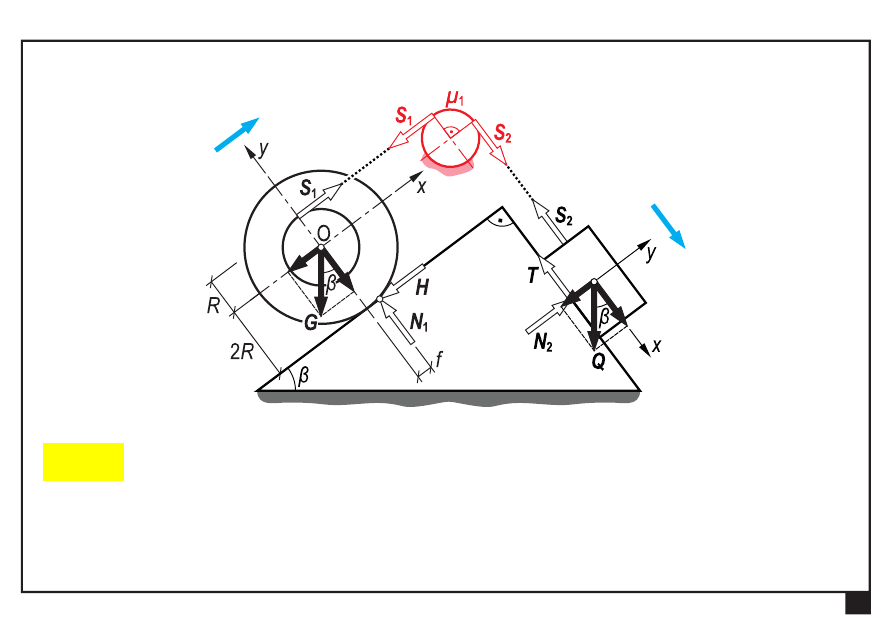
0

Σ



ix

P

 

0

sin

1







H

β

G

S

 (1) 

:

0

Σ



iy

P

 

0

cos

1





β

G

N

 (2) 

:

0

Σ

O



i

M

 

0

2

1

1













R

H

R

S

f

N

 (3) 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie — przykład  

 

 

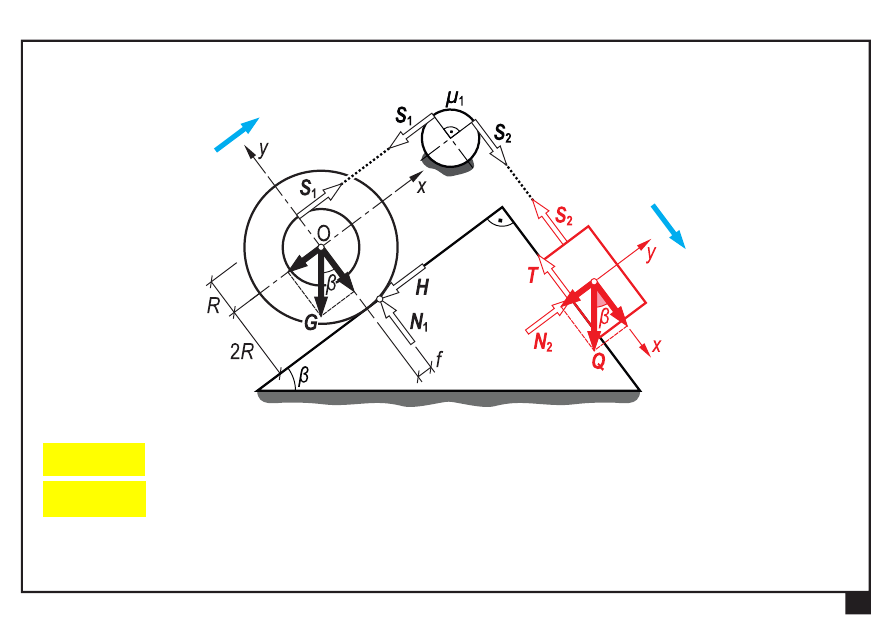
1

2

S

S 

 



1

e

2

1

μ

S

S





 (4) 

 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie — przykład  

 

 

:

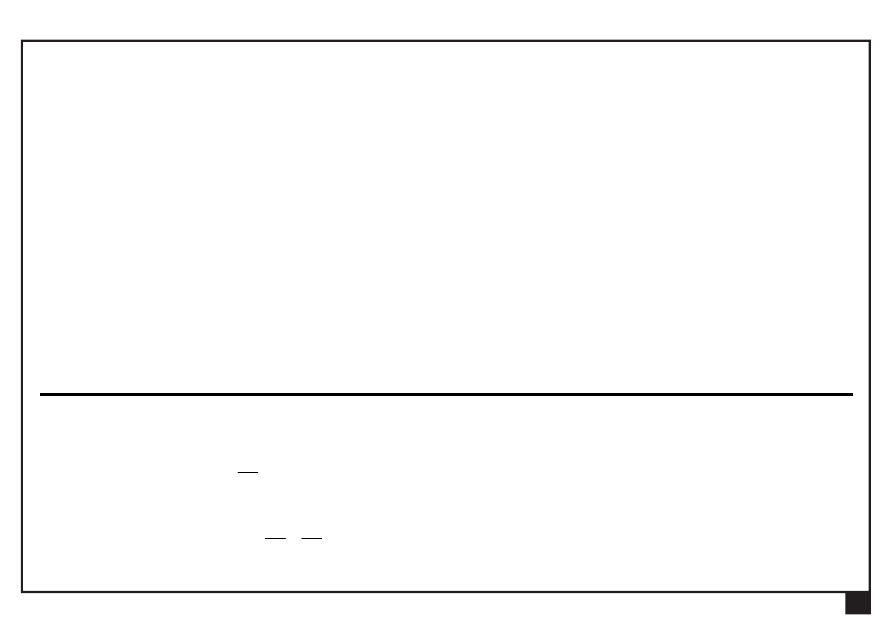
0

Σ



ix

P

 

0

cos

2







S

T

β

Q

 (5) 

:

0

Σ



iy

P

 

0

sin

2





β

Q

N

 (6) 

 

2

N

μ

T 

 (7) 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie — przykład  

0

sin

1







H

β

G

S

 (1) 

0

cos

1





β

G

N

 

(2) 

0

2

1

1













R

H

R

S

f

N

 (3) 



1

e

2

1

μ

S

S





 

(4) 

0

cos

2







S

T

β

Q

 (5) 

0

sin

2





β

Q

N

 

(6) 

2

N

μ

T 

 

(7) 

z (2): 

β

G

N

cos

1



 (8) 

(8) do (3): 

0

2

cos

1







H

S

β

R

f

G

 (9) 

(1) + (9) = 





















sin

cos

3 R

f

G

H

 (10) 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie — przykład  

0

sin

1







H

β

G

S

 (1) 

0

cos

1





β

G

N

 

(2) 

0

2

1

1













R

H

R

S

f

N

 (3) 



1

e

2

1

μ

S

S





 

(4) 

0

cos

2







S

T

β

Q

 (5) 

0

sin

2





β

Q

N

 

(6) 

2

N

μ

T 

 

(7) 

(10) do (9): 



























cos

sin

2

3

sin

1

R

f

G

H

G

S

 (11) 

z (6): 

β

Q

N

sin

2



 (12) 

(12) do (7): 

β

Q

μ

T

sin



 (13) 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie — przykład  

0

sin

1







H

β

G

S

 (1) 

0

cos

1





β

G

N

 

(2) 

0

2

1

1













R

H

R

S

f

N

 (3) 



1

e

2

1

μ

S

S





 

(4) 

0

cos

2







S

T

β

Q

 (5) 

0

sin

2





β

Q

N

 

(6) 

2

N

μ

T 

 

(7) 

(13) do (5): 

)

sin

(cos

2

β

μ

β

Q

S





 (14) 

(11) i (14) do (4): 



1

e

)

sin

(cos

cos

sin

2

3

μ

β

μ

β

Q

β

R

f

β

G





















 

 
 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie — przykład  

 



1

e

cos

sin

2

sin

cos

3

min

μ

Q

β

R

f

β

β

μ

β

G

G











 

 
po podstawieniu danych liczbowych otrzymujemy  

 

Q

Q

R

R

G

π

8836

,

0

e

5

4

05

,

0

5

3

2

5

3

5

,

0

5

4

3

2

2

,

0

min





































 

 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie — przykład  

 

 
Analogicznie wyznaczamy graniczną wartości ciężaru krążka 

max

G

.  

Bloczek o ciężarze Q porusza się do góry, natomiast krążek  
stacza się w dół 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie — przykład  

 



1

e

cos

sin

2

sin

cos

3

max

μ

Q

β

R

f

β

β

μ

β

G

G









 

 
po podstawieniu danych liczbowych otrzymujemy  

 

Q

Q

R

R

G

π

8949

,

3

e

5

4

05

,

0

5

3

2

5

3

5

,

0

5

4

3

2

2

,

0

max



































 

 

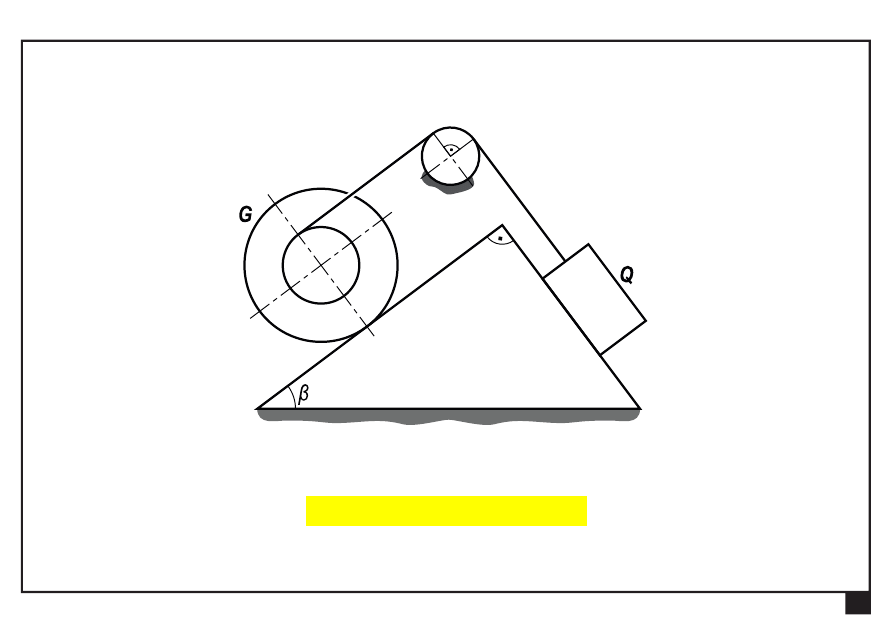
Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie — przykład  

 

 
układ będzie pozostawał w równowadze, jeśli spełnione będzie  

Q

G

Q

8949

,

3

8836

,

0





 

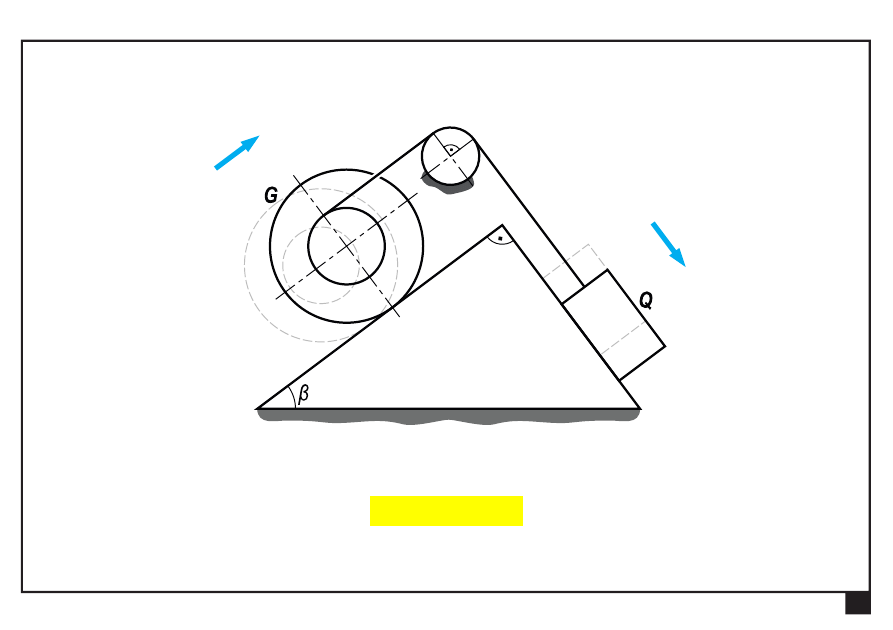
Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie — przykład  

 

 
układ będzie poruszał się „w prawo”, jeśli spełnione będzie  

Q

G

8836

,

0



 

 

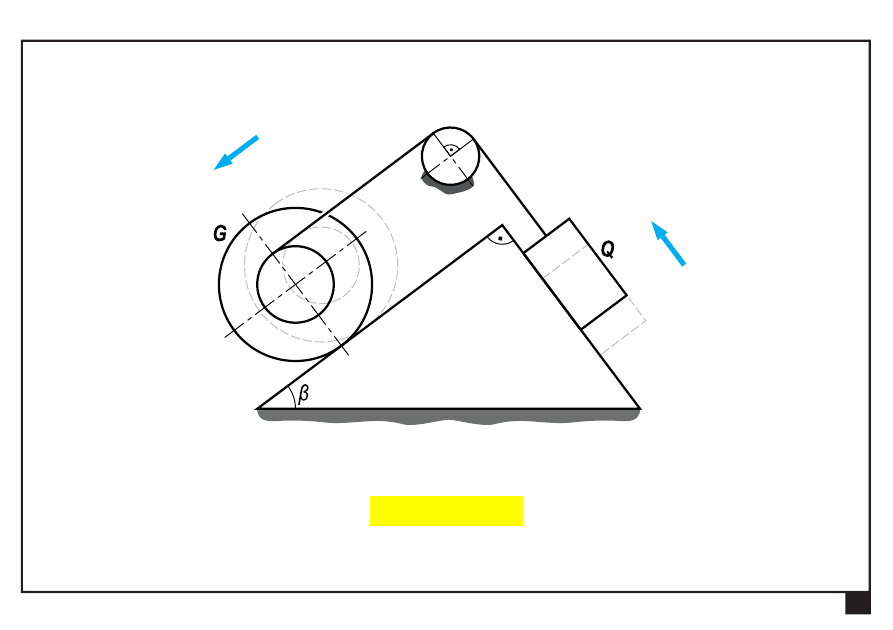
Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Tarcie — przykład  

 

 
układ będzie poruszał się „w lewo”, jeśli spełnione będzie  

Q

G

8949

,

3



 

Tarcie w układach płaskich.  

mechanika techniczna | statyka

 

4

 

Bibliografia  

Klasztorny M., Niezgoda T., Mechanika ogólna. Podstawy teoretyczne, 
zadania z rozwiązaniami, OW PW, Warszawa 2006. 
Klasztorny M., Mechanika ogólna, DWE, Wrocław 2005.