1

DirectX ▪ Env. Sphere

Kłaniam się. Po wielu wysiłkach i trudach wreszcie się udało, choć miałem poważne wątpliwości czy dopiszę ten artykulik
do końca. Dzisiaj mam nadzieję bardzo fajna i ciekawa sprawa, a mianowicie zastosujemy w praktyce to o czym wiemy już z
teorii. Mapowanie środowiskowe w naszym własnym wykonaniu. Jeśli do tej pory nie mieliście satysfakcji z
prezentowanych przykładów, bo były albo zbyt proste albo oparte na znanych od lat przykładach dzisiaj mam dla was dobrą
nowinę! Będzie od razu z grubej rury, czyli nie dosyć, że mapowanie środowiskowe liczone przez nas (w przeciwieństwie do
przykładu z DX SDK 8.0) to będzie to jeszcze robił shader. Lekcja jak pewnie widać po suwaku z boku dosyć długa ale
niezmiernie ciekawa. Ja też nie mogę się doczekać więc bez skrupułów zacznijmy od razu analizę kodu.

struct CUSTOMVERTEX
{
FLOAT x, y, z; // untransformed, 3D position for the vertex
FLOAT nx, ny, nz; // normal for vertex
DWORD color; // vertex color
FLOAT tx; // first texture coordiantes
FLOAT ty;
FLOAT tx1; // second texture coordinates
FLOAT ty1;
};

#define D3DFVF_CUSTOMVERTEX ( D3DFVF_XYZ | D3DFVF_NORMAL | D3DFVF_DIFFUSE |
D3DFVF_TEX2 )

Na początek oczywiście określamy nasz własny format wierzchołków. W dzisiejszym programie będzie on dosyć nietypowy
ponieważ dzisiaj użyjemy po raz pierwszy dwóch zestawów tekstur dla jednego wierzchołka. Taki zestawów nasz
wierzchołek może mieć nawet do ośmiu co daje nam do ręki bardzo potężne narzędzie w walce o wygląd naszego obiektu,
któremu możemy nałożyć osiem tekstur w zupełnie niezależny od siebie sposób. My dzisiaj będziemy potrzebować tylko
dwóch ponieważ dla potrzeb tutorialu zrobiłem pewne założenie, mające uatrakcyjnić nieco naszego dzisiejszego bohatera.
Niemal wszystkie programy przykładowe, pokazujące mapowanie środowiskowe po prostu nakładają na obiekt teksturę
świata, co powoduje, że jest on błyszczący i robi wrażenie nawet chromowanego, ale mi już się takie znudziły.
Postanowiłem, że nasz nie tylko będzie błyszczący, ale także będzie posiadał pewien wzór na modelu (coś jak polerowane
drewno). Dlatego też do naszych potrzeb wierzchołek posiądzie jeden zestaw współrzędnych, którym będzie obsługiwał
mapę świata i drugi, który posłuży do zmapowania na niego tekstury, która jest niejako naturalnym pokryciem obiektu - mam
nadzieję, że choć tym nasz program wyróżni się z pośród tysięcy innych. I jak widać na załączonym powyżej fragmencie
kodu nakażemy w strukturze wierzchołka przechowywanie dwóch zestawów współrzędnych tekstury (zwracam uwagę, żeby
pamiętać o kolejności danych wierzchołków!) oraz definicję typu, który zawiera stałą

D3DFVF_TEX2

mówiącą, że

wierzchołek posiada dwa zestawy tekstur. Reszta rzeczy chyba nie wymaga komentarza, ponieważ wałkowaliśmy to już
dziesiątki razy.

Inicjalizację całego urządzenia, jak to już mamy w tradycji odpuścimy sobie dzisiaj, ponieważ chyba od początku naszych
lekcji nic dokładnie się tam nie zmienia. Z ważniejszych rzeczy ustawiamy tam tylko stan urządzenia, który nakaże
uwidocznienie powierzchni rysowanych w kierunku przeciwnym do ruchu wskazówek zegara (stała

D3DCULL_CCW

) oraz

wyłączenie światła, aby nam nie zawadzało (

FALSE

).

HRESULT InitGeometry()
{
...
g_pMesh->CloneMeshFVF( 0L, D3DFVF_CUSTOMVERTEX, g_pd3dDevice, &g_pMeshClone );
g_pMesh = g_pMeshClone;

return S_OK;
}

Ważną rzeczą natomiast będzie dla nas inicjalizacja geometrii, którą będziemy wyświetlać. Wszystko oprzemy sobie na
naszej przedostatniej lekcji, która mówiła nam o ładowaniu plików *.x. Już wiemy jak mamy się nimi posługiwać, więc może
tego także nie będę szczegółowo omawiał, bo to mamy dokładnie w lekcji, o której wspomniałem wyżej. W funkcji
inicjującej geometrię InitGeometry() mamy także załadowanie dwóch tekstur - dobrze znane nam też już z szeregu lekcji.
Jedna z tych tekstur przedstawiać będzie to, co znajduje się tak naprawdę na obiekcie (jego powierzchnię) a druga zawierać
naszą osławioną już bardzo mapę środowiska. Po prawidłowym załadowaniu danych modelu i tekstur będziemy musieli
zrobić jeszcze tylko jedną, ale bardzo ważną rzecz. Ponieważ nasz obiekt używa dosyć nietypowego rodzaju wierzchołka,
który zawiera różne dziwne dane (dodatkowe współrzędne mapowania) a załadowane dane z pliku *.x takich nie posiadają,
więc koniecznym stanie się dopasowanie naszego obiektu typu

LPD3DXMESH

aby używał naszego, zdefiniowanego

formatu wierzchołków a nie tego załadowanego z pliku. Aby to zrobić posłużymy się dodatkowym obiektem tego samego
typu i wykorzystamy jedną z jego bardzo pożytecznych metod. Obiekt ten nazwiemy sobie dla przykładu g_pMeshClone a
metodą którą zechcemy wykorzystać będzie metoda obiektu siatki (wspomnianego

LPD3DXMESH

) o nazwie

CloneMeshFVF()

. Wprawdzie tak dokładnie i szczerze mówiąc jest to metoda obiektu, z którego dziedziczy nasz

2

DirectX ▪ Env. Sphere

wspomniany, ale jak wiemy w technologii COM obiekty są dziedziczone binarnie, ze wszystkimi niezmienionymi funkcjami
i dlatego też w obiekcie siatki nasza metoda występuje bez zmian, w stosunku do oryginału. A cóż takiego robi ta metoda?
Otóż, najprościej mówiąc kopiuje ona siatki, używając jednocześnie przy kopiowaniu w stosunku do nowej, naszego
własnego zdefiniowanego formatu wierzchołków. W naszym przykładzie metoda przyjmie następujące argumenty:
Pierwszym są opcje, z jakimi chcemy kopiować, w opisie SDK znajdziecie sporo różnych, a ponieważ nam nie zależy na
jakiś kosmicznych wynalazkach, więc aby domyślnie wszystko przebiegało ustawiamy go sobie na wartość zero. Drugim
parametrem jest nasz własny format wierzchołków, który zdefiniowaliśmy na początku programu i który zostanie
aplikowany nowo powstałej siatce. Trzecim już nam dobrze znane i jakże potrzebne urządzenia no a ostatnim wskaźnik do
obiektu siatki, do którego zostanie skopiowany ten, na rzecz którego wywołujemy tę metodę. Po utworzeniu nowego obiektu,
który zawiera już wierzchołki w naszym formacie aby nie wprowadzać za dużo zamieszania podmieniamy adres starego
obiektu na ten nasz nowy (no bo tak naprawdę to są wskaźniki pokazujące tylko określony obszar pamięci).

Kolejną rzeczą będzie skompilowanie i stworzenie naszego vertex shadera, który będzie służył do osiągnięcia naszego efektu
a w szczegółach do policzenia wektora refleksu i współrzędnych mapy świata. Nie będzie tutaj jakieś wielkiej filozofii i
może to także dzisiaj zostawimy sobie w spokoju - to jest wywołanie dwóch zaledwie funkcji i jest naprawdę bardzo
dokładnie omówione w lekcji poświęconej vertex shaderom, więc odsyłam właśnie tam. Sam shader zaś omówimy już
bardzo niedługo.

void SetupFrame()
{
...
// calculations for sphere mapping
D3DXMatrixMultiply( &matWorld, &matWorldX, &matWorldY );
D3DXMatrixMultiply( &matViewProj, &matView, &matProj );
D3DXMatrixInverse( &matInvView, NULL, &matView );
D3DXVECTOR4 vectPos( matInvView._41, matInvView._42, matInvView._43, 1.0 );
D3DXVECTOR4 vect( 0.0f, 0.5f, 1.0f, 2.0 );

g_pd3dDevice->SetVertexShaderConstant( 0, D3DXMatrixTranspose( &matWorld,
&matWorld ), 4 );
g_pd3dDevice->SetVertexShaderConstant( 4, D3DXMatrixTranspose( &matViewProj,
&matViewProj ), 4 );
g_pd3dDevice->SetVertexShaderConstant( 8, &vectPos, 1 );
g_pd3dDevice->SetVertexShaderConstant( 9, &vect, 1 );
}

Zanim jednak przejdziemy do jego omawiania, będziemy musieli dla niego określić pewne dane, które będą mu niewątpliwie
potrzebne. Przede wszystkim musimy mu przekazać macierze świata, widoku i projekcji aby mógł on przekształcać
wierzchołki. Po drugie będzie potrzebował położenia kamery, do policzenia pewnych danych (wszystko wyjaśni się
dokładniej przy jego opisie). I jeszcze dodatkowo do potrzeb wzorów na współrzędne map przekażemy do jego wnętrza
pewne stałe liczby. Wszystkie te dane podamy shaderowi za pomocą dobrze nam już znanej metody urządzenia

SetVertexShaderConstant()

. Metoda ta wszystkie wartości przez nią przekazywane będzie umieszczać jak wiemy w

rejestrach pamięci stałej, w zależności od ostatniego parametru będzie ich zajmować odpowiednią ilość. Zanim zaczniemy
jednak przekazywać shaderowi dane musimy je mieć. Po pierwsze macierze - dla oszczędności miejsca i pokazania w jaki
sposób to robić dzisiaj zrobimy sobie pewną sztuczkę. Jako pierwszą przekażemy macierz świata, bo ta musi nam jeszcze w
shaderze posłużyć do obliczeń. Jako drugą przekażemy macierz, która będzie złożeniem widoku i projekcji. Jak wiemy
doskonale złożenie macierzy pozwala uniknąć nakładu obliczeń i to właśnie mamy zamiar tutaj zrobić. Mnożymy więc te
dwie macierze przez siebie i umieszczamy w pamięci stałej. Mnożąc wierzchołek przez taką macierz otrzymamy przecież
dokładnie to samo, jak gdybyśmy mnożyli najpierw przez widok a później przez projekcję - a o ile mniej mnożeń mamy w
tym przypadku. Potrzebne do obliczeń będzie nam jeszcze położenie kamery. Ponieważ je podajemy jako bezpośredni
parametr do funkcji tworzącej macierz widoku

D3DXMatrixLookAtLH()

więc aby wyciągnąć potem jej położenie

odwrócimy sobie tą macierz i ostatnim wierszem tej odwróconej będzie właśnie nasze szukane położenie kamery. W
odwracanie macierzy oczywiście nie musimy się bawić sami, ponieważ jak zwykle biblioteka

D3DX

posłuży nam tutaj swoją

wielką pomocą. Funkcja

D3DXMatrixInverse()

jako swój pierwszy parametr przyjmie adres zmiennej, w której ma być

umieszczona nasza odwracana macierz, w drugim znajdzie się w razie powodzenia operacji odwracania - jej wyznacznik.
Ostatnim parametrem będzie adres macierzy, którą chcemy odwrócić czyli macierzy widoku. No i jak widać we fragmencie
kodu poniżej lecimy najpierw z macierzą świata, która zajmie rejestry od

c0

do

c3

, następnie przekażemy do shadera

wymnożone ze sobą macierze widoku i projekcji w rejestrach od

c4

do

c7

. A na końcu w pojedynczych rejestrach resztę

danych -

c8

będzie zawierał pozycję kamery, a

c9

kilka potrzebnych stałych liczbowych.

Mając przygotowane dane dla shadera i wypełniwszy jego rejestry tym, co mogliśmy na tym etapie czas przygotować się do
przetworzenia wierzchołków - czyli czas napisać deklarator dla rejestrów wejściowych i przystąpić do najważniejszej części
naszej lekcji - czyli napisania shadera, który odpowiednio przygotuje nam wierzchołki a precyzyjniej mówiąc jego głównym
zadaniem będzie policzenie zgodnie ze wzorami współrzędnych mapowania dla mapy świata (ale oczywiście nie tylko).

3

DirectX ▪ Env. Sphere

// vertex shader for sphere mapping
DWORD dwDecl[] =
{
D3DVSD_STREAM( 0 ),
D3DVSD_REG( D3DVSDE_POSITION, D3DVSDT_FLOAT3 ),
D3DVSD_REG( D3DVSDE_NORMAL, D3DVSDT_FLOAT3 ),
D3DVSD_REG( D3DVSDE_DIFFUSE, D3DVSDT_D3DCOLOR ),
D3DVSD_REG( D3DVSDE_TEXCOORD0, D3DVSDT_FLOAT2 ),
D3DVSD_REG( D3DVSDE_TEXCOORD1, D3DVSDT_FLOAT2 ),
D3DVSD_END()
};

Wprawdzie dokładną budowę deklaratora znamy z lekcji o shaderach, ale ponieważ jeszcze mało mieliśmy z tym do
czynienia, to przypomnijmy sobie to tak dokładniej. Pierwszą instrukcją naszego deklaratora określamy numer strumienia, z
którego będą pobierane nasze dane. Makro

D3DVSD_STREAM()

ustawia nam numer tego strumienia, który podamy jako

argument makra. Ponieważ u nas nie będziemy za dużo kombinować, więc jak zwykle ustawimy sobie numer naszego
strumienia na wartość zero.
Mając źródło danych możemy określić teraz jaka część tych danych trafi do jakiego rejestru. Makro

D3DVSD_REG()

kojarzy nam dane ze strumienia (elementy wierzchołków) z konkretnymi rejestrami wejściowymi shadera. Pierwszym
argumentem tego makra jest konkretny rejestr a drugim ilość danych, jakie do tego rejestru zostaną wpisane. Ze wszystkim
ma jeszcze oczywiście związek wcześniej zdeklarowany nasz własny typ wierzchołków, które determinuje kolejność danych
w strumieniu. I tym właśnie strumieniem popłyną:

D3DVSDE_POSITION, D3DVSDT_FLOAT3

- Najpierw pojawią się "na taśmie" trzy liczby określające pozycję wierzchołka,

stąd do rejestru określanego jako

D3DVSDE_POSITION

(tak naprawdę rejestr

v0

) trafią właśnie one. Nie jest to

oczywiście nakazem, ale my żeby nabrać dobrych przyzwyczajeń będziemy sobie umieszczali nasze dane w miejscach dla
nich przeznaczonych. Jeśli popiszecie więcej shaderów to przekonacie się, że znacznie to nam ułatwi sprawę i poszukiwanie
ewentualnych błędów.

D3DVSDE_NORMAL, D3DVSDT_FLOAT3

- zgodnie z definicją wierzchołka pojawią się następnie w strumieniu trzy liczby

określające normalną wierzchołka. Te wartości z kolei przechowamy sobie w rejestrze określanym jako

D3DVSDE_NORMAL

, co dla shadera będzie oznaczało fizyczny rejestr

v3

.

D3DVSDE_DIFFUSE, D3DVSDT_D3DCOLOR

- kolejne dane, to kolor wierzchołka, tym razem jako cztery liczby

float

z

zakresu 0.0 - 1.0. Stała

D3DVSDT_D3DCOLOR

określa właśnie je i trafią one do rejestru określonego jako

D3DVSDE_DIFFUSE

, czyli tak naprawdę do

v5

.

Przy omawianiu definicji wierzchołka powiedzieliśmy sobie o sposobie, w jaki będziemy tworzyć mapę środowiska.
Ponieważ chcemy sobie nasz przykład nieco urozmaicić więc oprócz błyszczącej powłoki dodamy naszemu obiektowi
jeszcze właściwą teksturę. Do tego celu będą nam potrzebne właśnie dwa zestawy współrzędnych mapowania. Ponieważ
format wierzchołków takie dwa zestawy nam definiuje deklarator obydwa z nich musi uwzględnić, żeby się wszystko
zgadzało:

D3DVSDE_TEXCOORD0, D3DVSDT_FLOAT2

- do rejestru odpowiedzialnego za współrzędne zestawu pierwszego

(

D3DVSDE_TEXCOORD0

czyli

v7

) zostaną przekazane dwie liczby typu

float

, ponieważ takie są nam potrzebne aby

określić współrzędne tekstury. I chociaż my tam jakieś wartości będziemy mieli, to tak naprawdę nie wykorzystamy ich w
żaden sposób, ponieważ zawartość rejestru wyjściowego

oT0

zostanie obliczona przez shader na podstawie innych danych.

Tę wartość wejściową za to wykorzystamy w przypadku drugiego zestawu, który określi położenie tekstury właściwej na
obiekcie.

D3DVSDE_TEXCOORD1, D3DVSDT_FLOAT2

- Do rejestru

D3DVSDE_TEXCOORD1

(czyli

v8

) przywędrują także jakieś

dane. Ale i tych ich nie wykorzystamy w żaden sposób, ponieważ tak naprawdę dane o teksturze przyjdą w rejestrze

v7

i to

właśnie z niego przepiszemy wartości do rejestru

oT1

. Ktoś pewnie sobie pomyśli, że sporo nakombinowałem, ale

potraktujcie to może jako dodatkowe ćwiczenie i możliwość optymalizacji naszego programu - będzie na pewno na czym
poćwiczyć ;). Wszystko dzieje się przez dwie rzeczy. Po pierwsze w programie do modelowania możemy określić tylko
jeden zestaw współrzędnych mapowania, a z kolei drugi nam potrzebny musi być na bieżąco obliczany. A że pierwszy jest
drugi i na odwrót - cóż ;). Jak wam się chce to możecie doprowadzić to do porządku, najważniejsze, abyście zrozumieli ideę.
Na sam koniec musimy jeszcze zamknąć nasz deklarator za pomocą makra

D3DVSD_END()

, które zakończy nasze

zmagania z danymi wejściowymi dla deklaratora.

Po zdefiniowaniu deklaratora czas przystąpić do napisania naszego shadera. Głównym założeniem jest to, aby shader policzył
na podstawie danych wejściowych współrzędne dla mapy środowiska. Algorytm generowania danych dla takiej mapy znamy,
sposób podawania i dane wejściowe mamy określone przez deklarator, czas więc przystąpić do dzieła:

vs.1.0

4

DirectX ▪ Env. Sphere

; r0: space position
; r1: space normal
; r2: vertex-eye vector
; r3: reflection vector
; r4: texture coordinates

; Transform position and normal into space
m4x4 r0, v0, c0
m3x3 r1, v3, c0

; Compute normalized view vector
add r2, c8,-r0
dp3 r3, r2, r2
rsq r3, r3
mul r2, r2, r3

; Compute space reflection vector
dp3 r3, r1, r2
mul r1, r1, r3
add r1, r1, r1
add r3,-r1, r2

; Compute sphere-map texture coords
add r3.z, r3.z, c9.z
dp3 r4, r3, r3
rsq r5, r4
mul r5, r5, c9.y

; Project position
m4x4 oPos, r0, c4
mov oT1, v7
mad oT0.xy, r3.xy, r5.xy, c9.y
mov oD0, v5

vs.1.0

Pierwszą rzeczą w shaderze jest oczywiście jego wersja. Tradycyjnie nadajemy mu już wartość 1.0 i tylko przypominam, że
instrukcja nadająca numer wersji shaderowi musi być pierwszą instrukcją w programie bo inaczej klapa.

m4x4 r0, v0, c0
m4x4 r1, v3, c0

Pamiętamy na pewno z lekcji o vertex shaderach w jaki sposób przekazywaliśmy macierze do wnętrza shadera. Poszczególne
macierze są ładowane poprzez rejestry pamięci stałej, po cztery dla każdej macierzy, której chcieliśmy użyć. W każdej
komórce pamięci stałej mamy oczywiście jak pamiętamy po cztery wartości typu

float

, co w sumie daje nam macierz.

Przeważnie wstawiane były one na początku tej pamięci, rejestrach zaczynających się od

c0

. Nie inaczej będziemy mieli w

naszym programie. Macierz świata zostanie umieszczona (co pokaliśmy w opisie kodu programu aplikacji) w rejestrach od

c0

do

c3

i za pomocą rejestru c0 będziemy się nią posługiwać. Skoro macierz będziemy mieli już w odpowiednich

rejestrach, więc będziemy mogli zacząć przekształcać naszą bryłę. Pozycja wierzchołka jak wiemy mieści się w rejestrze

v0

a makro

m4x4

spowoduje wymnożenie tego co jest w

v0

przez trzeci parametr tegoż makra, czyli to co znajduje się w

c0

.

Makro to oczywiście jako trzeciego argumentu spodziewa się macierzy 4x4, natomiast wynik takiego pomnożenia znajdzie
się nam w rejestrze tymczasowym

r0

. A co tam się znajdzie? Ci co uważnie śledzą i się uczą pilnie to oczywiście wiedzą -

będziemy tam mieć przekształconą przez macierz świata pozycję naszego wierzchołka, czyli de facto - umieszczoną bryłę
gdzieś w naszym świecie. Ponieważ do obliczeń współrzędnych mapowania mapy środowiska będzie nam potrzebny wektor
refleksu, a ten z kolei policzymy sobie z normalnej, więc aby te z kolei nie pozostawały za wierzchołkami, musimy je także
przekształcić przez macierz świata - są one przekazywane do shadera w swoim standardowym rejestrze

v3

. Wynik znajdzie

się w rejestrze tymczasowym

r1

jak dobitnie pokazuje nam powyższy kawałek kodu.

; Compute normalized view vector
add r2, c8,-r0
dp3 r3, r2, r2
rsq r3, r3
mul r2, r2, r3

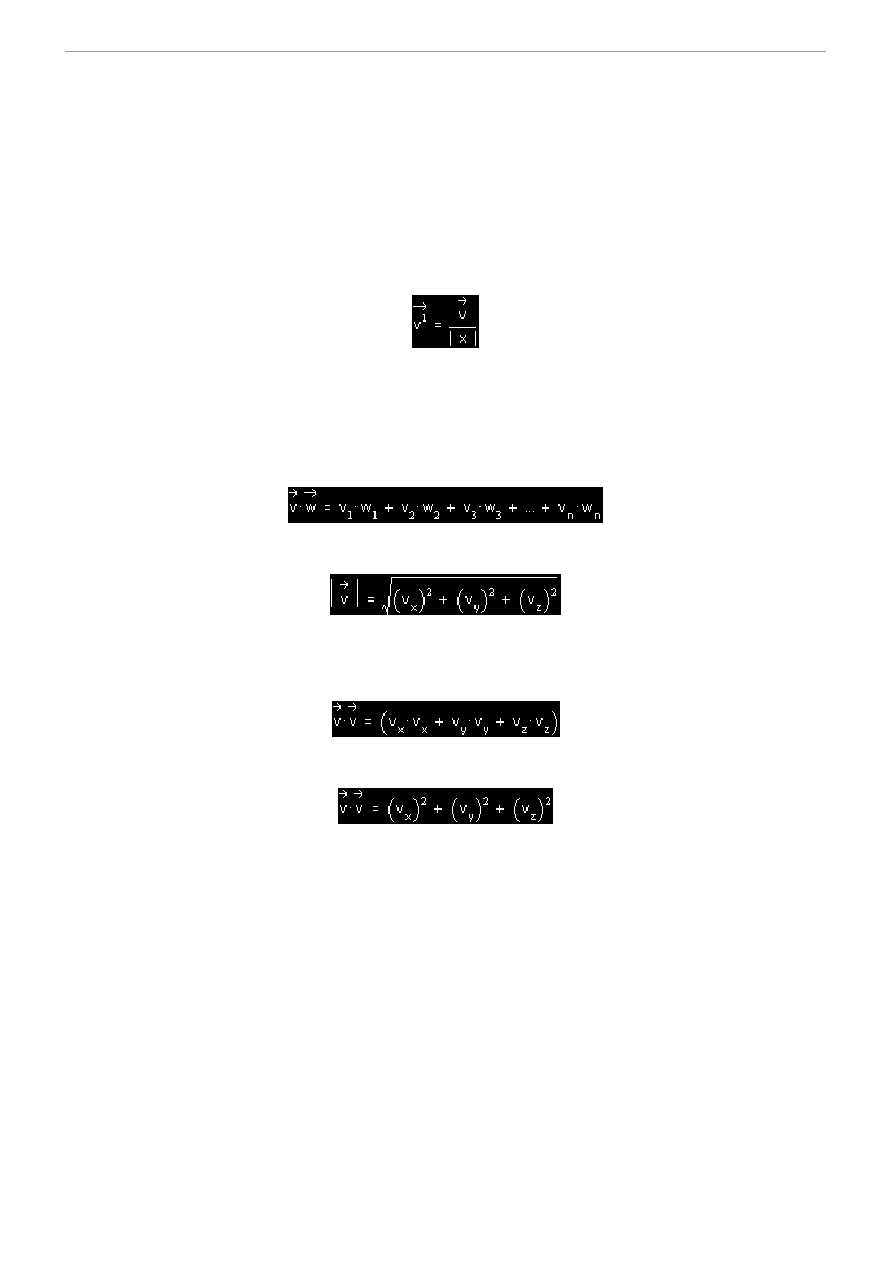
5

DirectX ▪ Env. Sphere

Mając naszą bryłę w świecie możemy przystąpić do konkretnych obliczeń potrzebnych nam elementów. Pierwszym z nich
będzie wektor widoku, łączący kamerę z konkretnym wierzchołkiem, który dodatkowo powinien być znormalizowany.
Pozycję kamery będziemy mieli z odwróconej macierzy widoku, jako jej ostatni wiersz. Odwrócony wektor z macierzy
widoku zapamiętamy w rejestrze pamięci stałej

c8

, który wypełniliśmy sobie odpowiednią funkcją w programie. Od niego

musimy odjąć pozycję wierzchołka, który musi być przekształcony przez macierz świata. Taki wierzchołek przed momentem
policzyliśmy sobie i przechowujemy go w rejestrze tymczasowym

r0

. Wyżej wymienione wektory my sobie dodamy, tylko

że jednemu z nich (temu, którego będziemy odejmować) zmienimy znak na przeciwny (możemy to zrobić bez użycia
żadnych specjalnych rozkazów). Wynik naszego działania umieścimy w rejestrze tymczasowym

r2

. Następnie musimy ten

nasz nowy obliczony wynalazek, który też będzie wektorem znormalizować aby posiadał on długość jeden. Gdybyśmy
posługiwali biblioteką

D3DX

załatwilibyśmy to sobie jedną sprytną funkcją, ale ponieważ my jesteśmy masochistami i

wolimy asembler, więc będziemy musieli sobie poradzić inaczej, co wcale nie znaczy, że gorzej. Przepis na normalizację
wektora znamy przecież doskonale:

gdzie v to wektor, który chcemy znormalizować a |v| to jego długość. Wektor do znormalizowania mamy w rejestrze

r2

,

natomiast co z tą długością? Jak ją policzyć mam nadzieję, że każdy już się dowiedział a jak nie to zapraszam do podstaw
matematyki. Mówiłem też wtedy niejako przy okazji o iloczynie skalarnym wektorów - to także jest w miarę proste do
zapamiętania, więc liczę, że zrozumiecie teraz mój wywód i to co zrobimy w shaderze. Skoro mówię o tych dwóch rzeczach,
to pewnie posłużą one nam w jakiś sposób do obliczenia tej szukanej długości. No i nie mylicie się na pewno. Zacznijmy
może od iloczynu skalarnego wektorów:

Teraz proponuję bardzo uważnie przyjrzeć się wzorowi na długość wektora v:

Cóż można wywnioskować z powyższej kombinacji - pod pierwiastkiem mamy tak jakby podniesiony nasz wektor do
kwadratu, prawda? Podniesiony do kwadratu, czyli tak naprawdę pomnożony przez siebie. A czy ta wartość pod
pierwiastkiem czegoś wam nie przypomina? Jeśli nie, to załóżmy sobie na przykład coś takiego:

czyli robimy iloczyn skalarny z dwóch identycznych wektorów. Przekształćmy sobie ten wzorek do trochę krótszej postaci:

Zupełnie oczywiste, prawda? Teraz już nie można nie zauważyć, że to co znajdzie się pod pierwiastkiem nie jest niczym
innym jak tylko iloczynem skalarnym naszego wektora przez samego siebie! I tę właśnie sztuczkę wykorzystamy bardzo
sprytnie w naszym shaderze. Jeśli dokładnie przetrząsnąć zasoby rozkazów vertex shadera to znajdziemy bardzo nam
przydatny, nie tylko dzisiaj rozkaz

dp3

. Rozkaz dokonuje iloczynu skalarnego wektorów, które podajemy jako parametry

drugi i trzeci a wynik w postaci liczby umieszcza w rejestrze, który jest parametrem numer jeden. Jeśli ten rozkaz wywołamy
w taki sposób jak w naszym shaderze:

dp3 r3, r2, r2

to widać, że wektorami (a raczej wektorem) biorącym udział w operacji iloczynu będzie ten nasz, który chcemy
znormalizować. Jeśli wstawimy jego dane do wzoru, według którego obliczany jest iloczyn skalarny to otrzymamy do ręki
nic innego, jak zawartość tego, co ma być pod pierwiastkiem do obliczenia długości!

rsq r3, r3

A co zrobić z obliczeniem pierwiastka? Rozkazem, który nam tutaj zaradzi będzie

rsq

, który choć może niedokładnie, ale

zaraz okaże się bardzo pomocny. Ma on dosyć specyficzne działanie - jeśli składowymi wektora są jedynki, wtedy wynikiem
całej operacji będzie wartość "1" w rejestrze docelowym, jeśli składowe mają wartość "0" to w rejestrze docelowym znajdzie
się pewna stała, która określać będzie nieskończoność. Najciekawiej jednak będzie się to wszystko zachowywać jeśli w
wektorze wejściowym znajdzie się dowolna inna wartość. Rozkaz

rsq

w takim przypadku policzy odwrotność pierwiastka z

6

DirectX ▪ Env. Sphere

tego, co podamy w rejestrze wejściowym. Po wykonaniu tych sądzę, że prostych i jak na razie całkowicie dla was
zrozumiałych operacji będziemy mieli wszystko co potrzeba do policzenia wektora znormalizowanego:
1. W rejestrze

r2

wektor, który chcemy znormalizować (jego współrzędne),

2 W rejestrze

r3

wartość, która de facto jest odwrotnością długości naszego wektora.

mul r2, r2, r3

A mając takie dane już z łatwością poradzimy sobie z naszą normalizacją za pomocą asemblera dostępnego w shaderze.
Wystarczy teraz zgodnie ze wzorem na wektor znormalizowany podzielić współrzędne wektora (lub pomnożyć przez
odwrotność!) przez jego długość, czyli przez pierwiastek. Czy już jest wszystko jasne? Myślę, że tak - pomnożenie
zawartości

r2

(współrzędne wektora) i

r3

(odwrotność długości) daje nam w wyniku wektor znormalizowany z rejestru

r2

,

który umieszczamy po przekształceniu go znowu w tym samym miejscu. Taką prostą w miarę kombinacją możemy sobie
bardzo szybko wektory normalizować i radzę ją dobrze zapamiętać, bo od dzisiaj już będziemy z niej bardzo często
korzystać.

; Compute camera-space reflection vector
dp3 r3, r2, r1
mul r1, r1, r3
add r1, r1, r1
add r3,-r1, r2

Następną rzeczą jaką musimy zrobimy to obliczyć nasz wektor refleksu, który będzie stanowić podstawę do wyliczenia
współrzędnych tekstur na bryle. W rejestrze

r1

mamy przekształcony przez macierz świata wektor normalny aktualnie

przerabianego przez shader wierzchołka natomiast w

r2

jest znormalizowany wektor widoku, łączący pozycję wierzchołka z

położeniem kamery. Jeśli przypomnimy sobie kolejne kroki w celu obliczenia wektora R z teorii to leci to tak:

Najpierw liczymy sobie zgodnie ze wzorem iloczyn skalarny wektorów v i n. V to znormalizowany przed momentem wektor
widoku, przechowywany w rejestrze

r2

. N to normalna wierzchołka, która cały czas tkwi w rejestrze

r1

. Ponieważ

obliczanie iloczynu skalarnego mamy przećwiczone w tej lekcji, więc nie będzie z tym już problemu:

dp3 r3, r2, r1

Wynik umieszczamy jak widać w rejestrze

r3

. Mając ten iloczyn skalarny jesteśmy już prawie w domu, no bo teraz zgodnie

ze wzorem dostaniemy już do ręki nasz upragniony wektor refleksu:

Ponieważ aż tak skomplikowanych operacji mi w shaderach nie możemy jeszcze robić, więc ten wzorek musimy sobie
podzielić na pewne etapy, żeby łatwiej nam to wszystko poszło a i dla karty było bardziej zjadliwe:

mul r1, r1, r3

W rejestrze

r3

mamy wynik iloczynu wektorów v i n. Najpierw pomnożymy sobie ten iloczyn przez wektor normalny

(rejestr

r1

). Wynik (czyi d*n), aby nie marnować miejsca i nie wprowadzać zamieszania z powrotem wędruje do rejestru

r1

.

Następnie należy pomnożyć otrzymaną wartość przez 2, aby otrzymać kombinację 2*d*n.

add r1, r1, r1

No tak, mieliśmy mnożyć, a tutaj co, dodawanie? Ano, możemy oczywiście sobie tutaj pomnożyć, nic nie stoi na
przeszkodzie. Ale powszechnie wiadomo, że zawsze mnożenie przez procesor jest troszeczkę wolniejsze niż dodawanie. A
ponieważ jesteśmy bardzo spostrzegawczy to zauważmy pewną właściwość a + a = 2a ! Banalne, prawda? Wynik ten sam, a
oszczędzamy być może kilka cykli na wierzchołku, co dla ich niemałych ilości idących ostatnio w grube tysiące jest nie do
pogardzenia. I znowu wynik operacji wędruje do rejestru

r1

. Na koniec, zgodnie ze wzorem na wektor R pozostaje nam

tylko odjąć od wektora V to co zostało po ostatniej operacji:

add r3,-r1, r2

Czyli dodajemy sobie ze zmienionym znakiem dla tej wartości, która ma zostać odjęta. Kogoś zapewne może rozdrażnić to,
że zamiast uczciwie używać rozkazu

sub

ja kombinuję coś ze zmianą znaków. Ano, przyznam się szczerze, że

przyzwyczaiłem się trochę do dodawania i mnożenia i jakoś ciągle nie mogę się nauczyć innych instrukcji shadera. Jeśli
kogoś to drażni to może sobie tutaj oczywiście zastosować odpowiedni rozkaz, nikogo nie zmuszam. A eksperymenty są

7

DirectX ▪ Env. Sphere

oczywiście jak najbardziej pożądane. Wynik naszego dodawanio-odejmowania jest umieszczony w rejestrze

r3

, który będzie

zawierał to, co tygrysy lubią najbardziej - nasz obliczony wektor refleksu.

; Compute sphere-map texture coords
mov r2, r3
add r3.z, r3.z, c9.z
dp3 r4, r3, r3
rsq r5, r4
mul r5, r5, c9.y

A skoro mamy to, czego szukaliśmy od bardzo dawna, czas to wykorzystać. Naszedł czas na wyznaczenie współrzędnych na
mapie świata, których użycie spowoduje że mapa ta będzie się zachowywać zgodnie z naszym życzeniem. Wróćmy do
tutorialiku prezentującego teorię mapowania sferycznego. Jak pamiętamy były tam takie oto trzy wzory:

Aby nie marnować czasu weźmy się od razu do dzieła. Po pierwsze musimy policzyć wartość, która znajduje się pod
pierwiastkiem. Jest to oczywiście iloczyn skalarny wektora refleksu z samym sobą, ale współrzędna Rz ma wartość
powiększoną o jeden. Zanim więc przystąpimy do kombinacji z pierwiastkami, najpierw dodamy sobie potrzebną jedynkę:

add r3.z, r3.z, c9.z

Dodajemy więc do zawartości składowej Rz wektora refleksu (składnik

r3.z

rejestru tymczasowego) wartość, którą

wypełniliśmy składową z rejestru pamięci stałej

c9

(ten zawiera kilka użytecznych stałych liczbowych, których używamy w

naszym shaderze). W tym przypadku w

c9.z

mieści się właśnie wartość jeden.

dp3 r4, r3, r3

Mając już tak przygotowany wektor możemy przystąpić do powtórzenia sztuczki z początku shadera, czyli pomnożenia
wektora przez samego siebie, w wyniku czego otrzymamy dokładnie to co pod pierwiastkiem. Robimy to oczywiście za
pomocą rozkazu

dp3

, któremu każemy pomnożyć dwa identyczne, a w zasadzie ten sam wektor - zmodyfikowany R. Wynik

pomnożenia zawędruje oczywiście do rejestru

r4

, jak widać. Mając tę wartość możemy ją wstawić pod pierwiastek.

Ponieważ w shaderze nie ma rozkazu liczącego bezpośrednio pierwiastek, a tylko taki odwrócony, więc wydawać by się
mogło, że znowu będziemy musieli ostro kombinować. Ale jeśli popatrzymy trochę w przód we wzory to znowu podziwiać
będziemy geniusz panów z M$. Przecież wartość, z którą przed momentem się uporaliśmy jest dokładnie mówiąc w
mianowniku! Więc nie będziemy musieli tego pierwiastka w żaden sposób przekształcać - tam gdzie go policzymy, tam on
zostanie! Liczmy więc:

rsq r5, r4

No oczywiste, wydaje mi się. Zmodyfikowany i podniesiony do kwadratu wektor R wędruje pod pierwiastek a ten z kolei do
mianownika ułamka, którego licznik stanowi jedynka. Pozostaje nam teraz tylko patrząc uważnie na wzory na współrzędne u
i v coś zrobić z tym ułamkiem, żeby wszystko się ładnie zgadzało.

mul r5, r5, c9.y

We wzorze na współrzędną mapy do licznika ułamka zawierającego pierwiastek zawędruje odpowiednia współrzędna
wektora refleksu. Do mianownika zaś wartość 2. A wartość 2 w mianowniku oznacza co? No właśnie - pomnożenie całości
przez 0.5 (lub 1/2 ;). A ponieważ mamy taką wartość w składowej

c9.y

więc nie czekając na nic wprowadźmy sobie to w

życie. Mnożymy zatem nasz odwrócony pierwiastek przez 0.5 i mamy w mianowniku 2*pierwiastek z wektora R, czyli
nawet więcej niż byśmy na razie chcieli - pierwiastek, pomnożony przez 2 już są w mianowniku!

; Project position
m4x4 oPos, r0, c4
mov oT1, v7
mad oT0.xy, r3.xy, r5.xy, c9.y
mov oD0, v5

8

DirectX ▪ Env. Sphere

Pozostaje jeszcze sprawa reszty ułamków. A ponieważ nasz shader dysponuje naprawdę bardzo przemyślanym i jak się bliżej
przyjrzeć nawet fantastycznym zestawem rozkazów to już nie zostało na wiele roboty. Resztę działań, aby już nie tracić
czasu wykonamy w końcowej części naszego shadera, w której będziemy ustalać dane wyjściowe. Ale może po kolei:

m4x4 oPos, r0, c4

Zaczynamy nie od współrzędnych mapowania (bo to nieładnie), ale od pozycji wierzchołków. Jak wiemy doskonale
rejestrem wyjściowym dla danych zawierających pozycję wierzchołka jest

oPos

. Nasz wierzchołek mamy jak do tej pory

przemnożony tylko przez macierz świata

c0

i znajduje się on w rejestrze

r0

. W rejstrach pamięci stałej od

c4

do

c7

mamy

zaś scaloną w jedno macierz widoku i projekcji. Scalenie oznacza po prostu ich pomnożenie w odpowiedniej kolejności - w
tym przypadku oczywiście najpierw macierz widoku a potem projekcji. Jeśli teraz pomnożymy wierzchołki ustawione w
świecie przez tą scaloną macierz to otrzymamy już współrzędne gotowe do wyświetlenia na ekranie.

mov oT1, v7

Ponieważ nasz obiekt ma trochę kombinowane tekstury dla osiągnięcia lepszego efektu, więc używamy dwóch zestawów
współrzędnych tekstur - mamy to dokładnie opisane w omówieniu aplikacji. Do rejestru drugiego zestawu, czyli

oT1

powędrują tym razem współrzędne, które są rzeczywistymi współrzędnymi tekstury na modelu - czyli takimi, jakie my
określiliśmy mu w trakcie jego tworzenia. Wiemy też, że rejestr

v7

jest odpowiedzialny za przechowywanie pierwszego

zestawu współrzędnych. Dlatego tutaj trochę kombinujemy - wczytujemy nasz model, który ma ustawione jakieś
współrzędne mapowania dla konkretnych wierzchołków. Pchamy to wszystko do shadera i on otrzymuje je w rejestrze
przeznaczonym do tego celu, czyli we wspomnianym już

v7

. Powinny one normalnie powędrować do rejestru

oT0

, ale

ponieważ jego używamy sobie do obliczania współrzędnych mapy za pomocą algorytmu, więc współrzędne właściwe
wędrują do

oT1

i za jego pomocą będą przekazane obiektowi. Ktoś może pomyśleć, że być może to zupełnie niepotrzebne

kombinacje, ale w treści shadera i tak musimy jawnie podać, co gdzie i dokąd idzie wiec w zasadzie jest to obojętne czy
zamienimy tutaj

oT0

z

oT1

. W każdym razie musimy zwracać tylko uwagę jaką teksturę przypiszemy do którego zestawu.

mad oT0.xy, r3.xy, r5.xy, c9.y

No i nadszedł czas na rozwiązanie ostatniej zagadki, czyli co resztą ułamków we wzorach na współrzędne mapy świata.
Wiemy, że brakuje nam w liczniku składowej wektora refleksu a do całości dodanej jeszcze wartość 1/2. Ale to jest już małe
piwo - mamy rozkaz, który załatwi nam to za jednym zamachem! Tak jak szalona jest rzecz, którą chcemy zrobić, tak samo
rozkaz - ma on szaloną nazwę

mad

;). W wielkim skrócie mówiąc rozkaz działa następująco: Posiada cztery argumenty -

pierwszy to przeznaczenie (wynik operacji). Dwa następne zostaną przez siebie pomnożone, a ostatni do nich po prostu
dodany. Naszym celem tutaj będzie pierwszy zestaw współrzędnych mapowania w rejestrze

oT0

. Jak wiemy w ułamku

pierwszym we wzorze na współrzędne mapowania brakuje nam składowych wektorów. I co w tym wszystkim
najśmieszniejsze, ale jednocześnie najwspanialsze, obie współrzędne podamy od razu! Składowa

oT0.x

będzie zawierać

współrzędną określaną przez wzór na u, natomiast

oT0.y

tę oznaczoną jako v. Wykorzystując możliwości shadera po prostu

w jednej instrukcji obliczymy wartości wynikające z dwóch wzorów - to tak, jakbyśmy właściwie wyniki przekazywali do
dwóch docelowych miejsc - czyż nie pięknie? Rejestr

r3

zawiera nadal nienaruszony wektor refleksu, a w zasadzie składowe

x i y (bo tylko te tak naprawdę nas interesują w tym momencie, a składowa z się zmieniała przecież). W rejestrze

r5

jeśli

dobrze pamiętamy mamy wartość jeden, podzieloną przez pierwiastek ze zmodyfikowanego wektora R, który dodatkowo jest
pomnożony przez 2 (wedle wymagań wzorów). Mnożąc te dwie wartości przez siebie otrzymujemy zatem pierwszy ułamek
w obu wzorach. Do pełni szczęścia brakuje nam tylko dodanie do całości wartości 0.5. Załatwia to ostatni argument, który
jest składową rejestru pamięci

c9.y

stałej zawierającym tę właśnie szukaną wartość.

mov oD0, v5

Aby być tak do końca porządnym należy jeszcze przekopiować do odpowiedniego rejestru kolor diffuse naszych
wierzchołków, ponieważ bez tego nasz shader będzie niekompletny a dobrych przyzwyczajeń nigdy dosyć. Tutaj jest już
wszystko standardowo - czyli z właściwego wejścia przekazujemy na właściwe wyjście.
No i to byłoby ma tyle samego shadera... ufff!, mam nadzieję, że wam się podobało? ;). Na pociechę dodam jednak, że to
jeszcze nie koniec...

g_pd3dDevice->BeginScene();
// Meshes are divided into subsets, one for each material. Render them in a loop
for( DWORD i=0; i < g_dwNumMaterials; i++ )
{
g_pd3dDevice->SetMaterial( &g_Material );
g_pd3dDevice->SetTexture( 0, g_pTexture );
g_pd3dDevice->SetTextureStageState( 0, D3DTSS_COLORARG1, D3DTA_TEXTURE );
g_pd3dDevice->SetTextureStageState( 0, D3DTSS_COLORARG2, D3DTA_DIFFUSE );
g_pd3dDevice->SetTextureStageState( 0, D3DTSS_COLOROP, D3DTOP_SELECTARG1);
g_pd3dDevice->SetTextureStageState( 0, D3DTSS_ALPHAOP, D3DTOP_DISABLE );
g_pd3dDevice->SetTextureStageState( 0, D3DTSS_MINFILTER, D3DTEXF_LINEAR );

9

DirectX ▪ Env. Sphere

g_pd3dDevice->SetTextureStageState( 0, D3DTSS_MAGFILTER, D3DTEXF_LINEAR );

g_pd3dDevice->SetTexture( 1, g_pTexture1 );
g_pd3dDevice->SetTextureStageState( 1, D3DTSS_COLORARG1, D3DTA_TEXTURE );
g_pd3dDevice->SetTextureStageState( 1, D3DTSS_COLORARG2, D3DTA_CURRENT );
g_pd3dDevice->SetTextureStageState( 1,D3DTSS_COLOROP, D3DTOP_BLENDTEXTUREALPHA
);
g_pd3dDevice->SetTextureStageState( 1, D3DTSS_ALPHAOP, D3DTOP_DISABLE );
g_pd3dDevice->SetTextureStageState( 1, D3DTSS_MINFILTER, D3DTEXF_LINEAR );
g_pd3dDevice->SetTextureStageState( 1, D3DTSS_MAGFILTER, D3DTEXF_LINEAR );
g_pd3dDevice->SetVertexShader( VertexShader );
LPDIRECT3DVERTEXBUFFER8 pVB;
LPDIRECT3DINDEXBUFFER8 pIB;

g_pMesh->GetVertexBuffer( &pVB );
g_pMesh->GetIndexBuffer( &pIB );
g_pd3dDevice->SetStreamSource( 0, pVB, sizeof( CUSTOMVERTEX ) );
g_pd3dDevice->SetIndices( pIB, 0 );
g_pd3dDevice->DrawIndexedPrimitive(D3DPT_TRIANGLELIST, 0, g_pMesh-
>GetNumVertices(), 0, g_pMesh->GetNumFaces());

}
g_pd3dDevice->EndScene();

Na sam koniec zostawiliśmy sobie więc najsmaczniejszy kąsek w całych tych naszych rozważaniach. Mamy już wszystko
pięknie policzone, przygotowane, załadowane - czas aby więc coś narysować! Do roboty więc idzie nasza funkcja
renderująca. Po wyczyszczeniu okienka możemy rozpocząć rysowanie (przypominam, że wszystko dzieje się pomiędzy
wywołaniem metod urządzenia

BeginScene()

i

EndScene()

. Jak pamiętamy z lekcji o ładowaniu plików *.x model może

posiadać więcej niż jedną nałożoną na siebie teksturę. Dlatego też będziemy rysować wszystko w pętli, która będzie
sterowana tak naprawdę przez ilość materiałów (tekstur) jakie model posiada. Dla każdego nowego materiału zostanie
narysowana nasza bryła z odpowiednią teksturą w odpowiednim miejscu. Już doskonale wiemy, jak nasz model będzie
wyglądał. Jedna tekstura będzie jego naturalnym pokryciem (czyli potrzebny nam będzie na pewno jeden poziom tekstur), a
odbijające się w nim otoczenie zasymulujemy odpowiednio drugą (czyli poziom drugi). Tekstura materiału pokrywającego
obiekt zostanie wyposażona dodatkowo w kanał przeźroczystości alfa, który umożliwi prześwitywanie mapy otoczenia przez
materiał dając złudzenie, że materiał jest dosyć metaliczny. Na pierwszym poziomie, oznaczonym jako "0" za każdym
przebiegiem pętli umieszczać będziemy teksturę, która niezmiennie będzie mapą otaczającego świata. Dokonamy tego za
pomocą doskonale nam znanej metody urządzenia -

SetTexture()

, która przypisze teksturę (argument drugi) do

odpowiedniego poziomu, podanego jako argument pierwszy. Następnie mamy szereg wywołań metody, która, jak także
dobrze wiemy poustawia nam tak urządzenie, że osiągniemy określony efekt przy manipulacji teksturą dla danego poziomu.
Na poziomie nie za wiele będziemy kombinować ale po kolei idąc to tak:

D3DTSS_COLORARG1, D3DTA_TEXTURE

- najpierw przeprowadzimy operację koloru. Pierwszym argumentem dla niej

będzie kolor tekstury,

D3DTSS_COLORARG2, D3DTA_DIFFUSE

- drugim zaś kolor diffuse wierzchołków.

D3DTSS_COLOROP, D3DTOP_SELECTARG1

- mając obydwa argumenty możemy określić rodzaj operacji na nich

wykonywanej, tutaj stała

D3DTOP_SELECTARG1

mówi nam tylko tyle, że jako wyjściowy element koloru na tym

poziomie otrzymamy to co jest na teksturze (bo ona jest argumentem nr 1), zupełnie więc bez uwzględniania koloru
wierzchołków. Swoją drogą znaleźliśmy dziurę w programie i możemy szukać tutaj jakiś optymalizacji usuwając na przykład
linię z deklaracja drugiego parametru dla operacji koloru - zawsze to parę niezwykle cennych dla nas ułamków sekundy.

D3DTSS_ALPHAOP, D3DTOP_DISABLE

- mając operację koloru czas określić rodzaj mieszania, jaki będzie przeprowadzony

dla poziomu nr "0". Tutaj jak widać wyłączamy go, ponieważ nic mieszać nie będziemy (jakby jeszcze mało było;).

D3DTSS_MINFILTER, D3DTEXF_LINEAR

D3DTSS_MAGFILTER, D3DTEXF_LINEAR

- i na koniec oczywiście ustawienie filtrowania tekstur, żeby pozbyć się na

ekranie pikselozy - to nasz akcelerator potrafi naprawdę robić bardzo szybko i dokładnie.
Po ustawieniu wszystkich parametrów dla poziomu pierwszego czas na poziom drugi, na którym znajdzie się mapa obiektu.

D3DTSS_COLORARG1, D3DTA_TEXTURE

- czyli znowu pierwszy argument operacji koloru.

D3DTSS_COLORARG2, D3DTA_CURRENT

- drugi do kolekcji. Tym razem dla poziomu nr "1" jest to to, co przychodzi z nr

"0", czyli tak naprawdę kolor tekstury reprezentującej środowisko (bo to było wynikiem operacji koloru na poprzednim
poziomie).

10

DirectX ▪ Env. Sphere

D3DTSS_COLOROP, D3DTOP_BLENDTEXTUREALPHA

- czyli nasza operacja koloru - tym razem już nie będzie tak prosto ale

za to bardzo efektownie. Nasza tekstura umieszczona na poziomie drugim będzie posiadała taki prawdziwy kanał alfa
(umieszczona jest w pliku o formacie *.tga, który potrafi taki przechowywać). I zgodnie ze wzorem:

na tym poziomie zostanie przeprowadzona operacja według podanego wzoru. Z tekstury, którą przekażemy urządzeniu jako
parametr pierwszy zostanie pobrany współczynnik alfa (przeźroczystości) i na jego podstawie zostaną obliczone kolory
pikseli na obiekcie. Jest to najbardziej typowe równanie dla blendingu i efekt jego zastosowania jest dosyć łatwy do
przewidzenia. Im współczynnik alfa będzie większy tym tekstura, która przychodzi będzie mniej przeźroczysta. Na obiekcie
będzie widać miejsca mniej i bardziej przeźroczyste - to nam dodatkowo podniesie atrakcyjność sceny.

D3DTSS_ALPHAOP, D3DTOP_DISABLE

- ponieważ sam kanał alfa w teksturze przychodzącej namiesza nam dosyć na naszej

scenie wiec i na poziomie drugim nic już więcej mieszać nie będziemy i wyłączymy sobie na wszelki wypadek taką
możliwość.

D3DTSS_MINFILTER, D3DTEXF_LINEAR

D3DTSS_MAGFILTER, D3DTEXF_LINEAR

- myślę, że tym razem już nie wymaga to komentarza.

g_pd3dDevice->SetVertexShader( VertexShader );

Ustawienie wszystkich stanów urządzenia oznacza ni mniej ni więcej tyle, że jesteśmy gotowi przekazać wszystkie potrzebne
dane naszemu shaderowi, nad którym tyle biedziliśmy się dzisiaj i w końcu go uruchomić. Powyższa, niepozorna metoda
urządzenia nakaże mu w stosunku do każdego od teraz obrabianego wierzchołka skorzystanie z naszego shadera a nie ze
standardowej procedury obsługi.

LPDIRECT3DVERTEXBUFFER8 pVB;
LPDIRECT3DINDEXBUFFER8 pIB;

g_pMesh->GetVertexBuffer( &pVB );
g_pMesh->GetIndexBuffer( &pIB );
g_pd3dDevice->SetStreamSource( 0, pVB, sizeof( CUSTOMVERTEX ) );
g_pd3dDevice->SetIndices( pIB, 0 );
g_pd3dDevice->DrawIndexedPrimitive(D3DPT_TRIANGLELIST, 0, g_pMesh-
>GetNumVertices(), 0, g_pMesh->GetNumFaces());

Ponieważ trochę kombinowaliśmy z naszymi wierzchołkami (podmienialiśmy ich format po załadowaniu z pliku *.x) więc
nie możemy sobie skorzystać za bardzo ze standardowej metody siatki do jej rysowania i musimy wrócić do starych, dobrych
prymitywów. Aby jednak to było możliwe będziemy musieli wydobyć z obiektu siatki dwie rzeczy - wierzchołki, z których
jest zbudowana oraz listę indeksów do nich. Indeksy będą mówić który wierzchołek z którym tworzyć będzie poszczególne
trójkąty (o indeksowaniu pisałem już w którejś z pierwszych naszych lekcji). Aby mieć gdzie przechować te dane, które
wykradniemy urządzeniu potrzebować będziemy dwóch buforów - jednego na wierzchołki (typu

LPDIRECT3DVERTEXBUFFER8

) oraz na wyżej wymienione indeksy (typ

LPDIRECT3DINDEXBUFFER8

). Mając

zadeklarowane te zmienne wywołamy sobie dwie uwidocznione powyżej metody obiektu siatki. Pierwsza,

GetVertexBuffer()

zwróci nam w swoim parametrze bufor, w którym przechowuje dane swoich wierzchołków. Jak łatwo się

domyślić metoda

GetIndexBuffer()

da nam drugą pożądaną przez nas rzecz czyli indeksy naszych wierzchołków. Kogoś

może przez moment zastanawiać, czemu nie ustalamy żadnych rozmiarów tych buforów - otóż obiekt siatki sam je doskonale
przecież zna i nas może to w ogóle nie interesować (bo i po co) - skoro dostajemy do ręki dane, to nic, tylko się cieszyć.
Skoro mamy bufor z wierzchołkami, znamy ich rozmiar (bo są one w naszym, ustalonym, wcześniej formacie przecież) więc
możemy ustawić źródło danych, z którego będzie czerpał vertex shader przy obrabianiu wierzchołków - metoda urządzenia

SetStreamSource()

wybitnie nam w tym wszystkim pomoże. Korzystaliśmy z niej już przecież wielokrotnie a jej wywołanie

powinno być dobrze znane. Pierwszy argument to numer strumienia, którym niezmiennie od początku pozostaje u nas "0",
drugi to fizyczne dane (czyli skradzione siatce wierzchołki) no a ostatni to rozmiar pojedynczej paczki (w zasadzie jednego
wierzchołka). W tym momencie shader już w zasadzie wie, skąd będzie czerpał dane do swojej pracy. Metoda

SetIndices()

ustawia dla D3D zbiór indeksów (które także mamy w buforze). Pierwszym parametrem będzie jak widać powyżej nasz zbiór
a drugim liczba, która w zasadzie tutaj nam się nie przyda. Umożliwia ona na upakowanie danych kilku brył zawierających
indeksy wierzchołków w jeden bufor wierzchołków. Przy renderingu konkretnej bryły trzeba potem odpowiednio
manipulować tym właśnie parametrem, żeby dobrać się to tej właściwej, którą mamy zamiar narysować. Ale ponieważ my
mamy jedną bryłę i to w miarę prostą więc nie musimy nic kombinować. Jak w większości przypadków wartość "0" oznacza
dla nas po prostu początek - i niech tak na razie zostanie.
No i cóż... w zasadzie pozostała nam już tylko jedna rzecz - nakazanie naszemu urządzeniu narysowanie długo oczekiwanej
przez nas bryły. Więc wywołujemy dosyć nową dla nas metodę, czyli

DrawIndexedPrimitive()

. Co ona robi, to za chwilę

już zobaczymy na ekranie, a wszystkie parametry tej metody powinny być nam już doskonale znane. Jako rysowany
prymityw posłuży nam dzisiaj typ określany jako

D3DPT_TRIANGLELIST

, czyli lista trójkątów -czyli po prostu

poszczególne trójkąty rysowane po kolei, do tej pory przecież właśnie na tym się opieraliśmy. Jako drugi parametr podajemy

11

DirectX ▪ Env. Sphere

numer pierwszego indeksu, ze zbioru w którym znajdują się wszystkie definiujące nasze trójkąty. Jak wspomniałem bryła i
scena bardzo prosta, więc na razie zaczynamy zawsze od wartości "0", żeby nie namieszać za dużo. Następny parametr
g_Mesh->GetNumVertices() to też chyba jest oczywiste - liczba wierzchołków, które zawarte są w obiekcie siatki.
Powyższe wywołanie takiej metody siatki zwraca potrzebną nam wartość. Następne znowu wartość "0" - tak, tak ;) - tym
razem udajemy się na początek zbioru wierzchołków. Ostatnim argumentem jest ilość prymitywów jakie będziemy rysować a
ponieważ rysujemy trójkąty więc oczywiście musimy wiedzieć, ile ich będzie. I tutaj także przychodzi nam z pomocą
nieoceniony obiekt siatki - czymże by był, gdyby nie zawierał metody

GetNumFaces()

, która zwraca oczywiście to co nam

potrzebne.
Pomniejsze fragmenty, które nie mają wielkiego wpływu na program, albo te, których omawianie po raz n-ty też wielkiego
sensu nie ma pominąłem. A jeśli niczego ważnego nie zgubiliśmy po drodze i wszystko (jak zawsze ;) się udało, oto co
zobaczymy na ekranie: