2. Interpretacja probabilistyczna mechaniki kwantowej, zasada nieoznaczoności

Heisenberga i ich ilustracja na przykładzie cząstki uwięzionej w studni potencjału.

INTERPRETACJA PROBABILISTYCZNA.

Na przykładzie elektronu chcemy zilustrować jak można zjednoczyć opis korpuskularny i
falowy.

Przeprowadzamy eksperyment:

Wiązkę elektronów przepuszczamy przez szczelinę o
szerokości Δx. Elektron przechodzi przez szczelinę i
zostaje ugięty przez szczelinę. Na ekranie powstaje
obraz

dyfrakcyjny,

którego

natężenie

jest

proporcjonalne do kwadratu amplitudy.

Jeśli potraktujemy elektron jak falę i przyjmiemy, że
jego amplituda wynosi Ψ, wtedy dla położenia x na
ekranie w chwili t natężenie będzie wynosiło:
𝐼 = |𝛹(𝑥, 𝑡)|

2

.

Ekran może być traktowany jako przyrząd służący do detekcji pojedynczych elektronów jako
cząstek. Ekran fluorescencyjny rozbłyskuje za każdym razem w punkcie, w którym uderza w
niego elektron. Tym samym elektron jest silnie zlokalizowany i nie powstaje obraz dyfrakcyjny.
Powtarzając doświadczenie obserwujemy rozbłyski w różnych punktach na ekranie. Jedynie,
gdy przeprowadzimy wiele doświadczeń z jednym elektronem lub pozwolimy przejść przez
szczelinę wielu elektronom, zaobserwujemy obraz dyfrakcyjny. Odgrywa to główną rolę w
zjawisku dualizmu korpuskularno-falowego. Z jednej strony natężenie na obrazie
dyfrakcyjnym w objętości ΔV jest proporcjonalne do kwadratu wartości bezwzględnej
amplitudy, a z drugiej jest proporcjonalne do prawdopodobieństwa znalezienia elektronu w
objętości ΔV. Zgodnie z podstawowym postulatem teorii prawdopodobieństwa suma
wszystkich prawdopodobieństw musi być równa 1. Ponieważ trafienie elektronu w dowolny
punkt ekranu jest tak samo prawdopodobne, wszystkie prawdopodobieństwa muszą być takie
same. Jeśli wykonany całkowanie po wszystkich punktach przestrzeni to cząstka musi gdzieś
zostać odnaleziona, a więc całkowite prawdopodobieństwo musi wynosić 1.

Interpretacja probabilistyczna funkcji falowej jest niezbędna, gdyż jeżeli uderzenie elektronu
w ekran wywołałoby jego rozbłysk to oznaczałoby to, że elektron się podzielił, a elektron jest
NIEPODZIELNY. Jeśli znajdziemy elektron w jednym miejscu, to jesteśmy pewni, że nie ma
go jednocześnie w innym miejscu.

ZASADA NIEOZNACZONOŚCI HEISENBERGA.

Zasada nieoznaczoności Heisenberga jest konsekwencją faktu, że elektron czasami zachowuje
się jak cząstka, a czasem jak fala.

„Niemożliwe jest równoczesne dokładne określenie pewnych par wielkości fizycznych układu,

do opisu którego stosuje się mechanikę kwantową.”

Zasada nieoznaczoności opisuje jedną z podstawowych własności przyrody. Pojawia się ona
wtedy, gdy opis zachowania cząstek w mikroświecie chcemy przeprowadzić używając pojęć

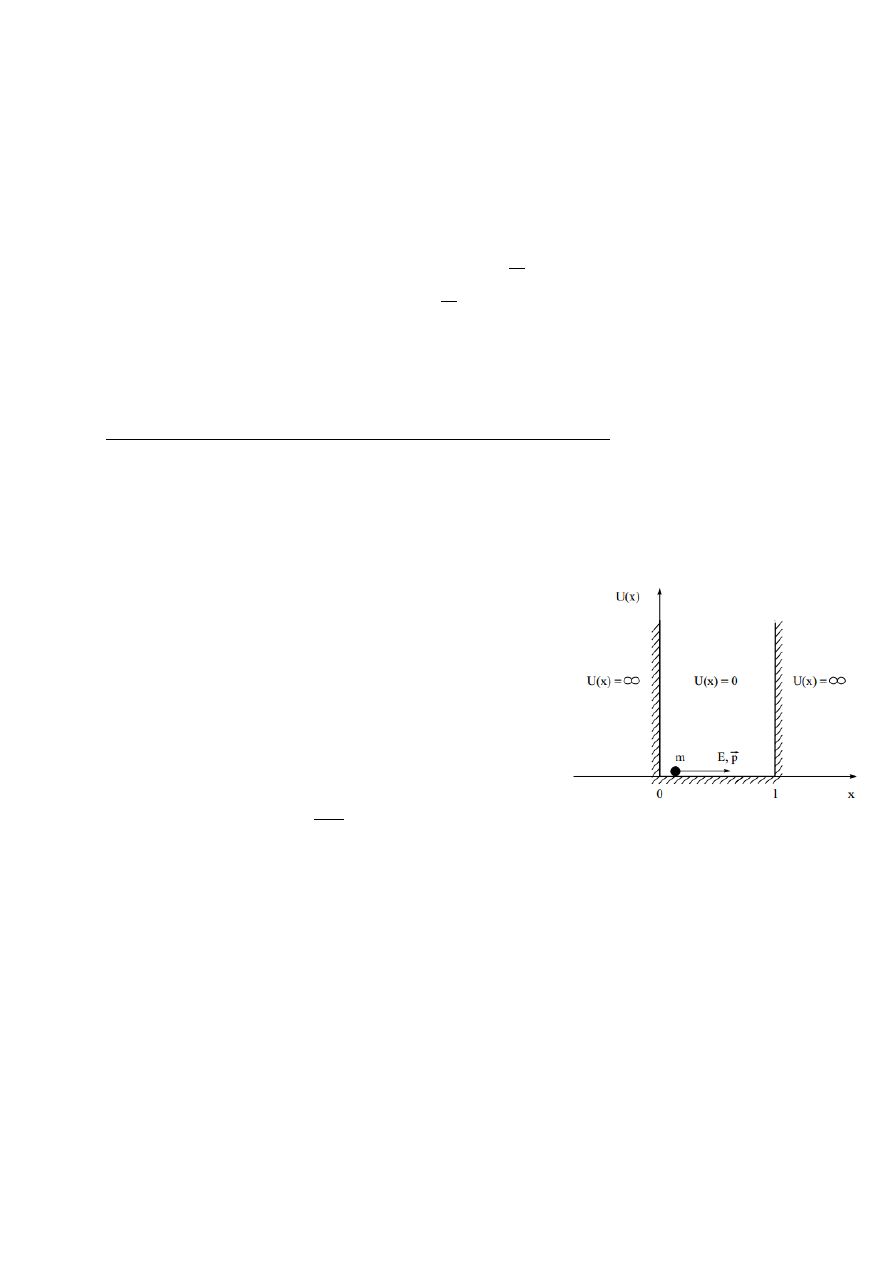
wziętych z makroświata. Zasada nieoznaczoności mówi o tym, że pewnych wielkości
fizycznych nie można zmierzyć jednocześnie z dowolną dokładnością. O wielkościach tych
mówi się, że nie komutują. Taką własność mają położenie i pęd oraz energia i czas. Z im
większą dokładnością znamy pęd cząstki, tym mniejsza jest dokładność określenia położenia.
Najczęściej zasadę nieoznaczoności Heisenberga przedstawiamy w postaci dwóch
nierówności:



jednej dla pędu i położenia cząstki:

𝛥𝑝

𝑥

∗ 𝛥𝑥 ≥

ℎ

4𝜋



drugą – dla energii i czasu:

𝛥𝐸 ∗ 𝛥𝑡 ≥

ℎ

2𝜋

,

gdzie: h=6,63*10

-34

J*s – stała Plancka.

Zasady nieoznaczoności nie warto stosować dla obiektów makroskopowych – niepewności są
nieosiągalne. Inaczej wygląda to natomiast w świecie atomów.

PRZYKŁAD CZĄSTKI UWIĘZIONEJ W STUDNI POTENCJAŁU.

Umieszczamy cząstkę w polu sił o energii potencjalnej określonej wzorem:

𝑈(𝑥) = { 0 𝑑𝑙𝑎 0 ≤ 𝑥 ≤ 𝑙

∞ 𝑑𝑙𝑎 𝑥 < 0 𝑖 𝑥 > 𝑙

,

czyli w tzw. studni potencjału o nieskończonej głębokości.

Z klasycznego punktu widzenia cząstka porusza się w
studni potencjału ruchem jednostajnym, odbijając się
kolejno od jej ścianek. Jeśli weźmiemy pod uwagę odbicia
fal de Broglie’a od ścian studni rozwiązanie równania
Schrodingera jest sumą fal poruszających się w kierunku
osi x. Funkcję falową wewnątrz studni określa wzór:

𝛹(𝑥) = 𝐴𝑒

𝑖𝑘𝑥

+ 𝐵𝑒

−𝑖𝑘𝑥

dla

0 ≤ 𝑥 ≤ 𝑙. Prawdopodobieństwo znalezienia cząstki na

zewnątrz studni powinno wynosić 0. Energia cząstki

określona jest wzorem:

𝐸 =

ℎ

2

𝑘

2

2𝑚

i w studni potencjału jest

skwantowana. Minimalna energia cząstki w studni potencjału musi być większa od zera.
Zgodnie z klasyczną mechaniką można stwierdzić, że cząstka w studni potencjału nie może
znajdować się w spoczynku, lecz porusza się swobodnie. Jest to ogólna własność rozwiązania
R.S., opisującego ruch cząstki w ograniczonym obszarze (minimalną energię nazywamy
energią zerową). Konieczność występowania zerowej energii można wytłumaczyć posługując
się zasadą nieoznaczoności. Jeżeli cząstka jest zamknięta w studni potencjału o szerokości l,
nieoznaczoność jej położenia ma skończoną wartość

𝛥𝑥 = 𝑙. Gdyby energia kinetyczna cząstki,

a co za tym idzie także pęd cząstki były równe 0, nieoznaczoność jej pędu wyniosłaby 0. Ale
wtedy iloczyn

𝛥𝑥 ∗ 𝛥𝑝 = 0 byłby sprzeczny z zasadą nieoznaczoności. Największe

prawdopodobieństwo znalezienia cząstki jest w miejscu, gdzie funkcja gęstości
prawdopodobieństwa przyjmuje największe wartości.