M08/5/MATHL/HP2/ENG/TZ1/XX/M+

16 pages

MARKSCHEME

May 2008

MATHEMATICS

Higher Level

Paper 2

– 2 –

M08/5/MATHL/HP2/ENG/TZ1/XX/M+

This markscheme is confidential and for the exclusive use of
examiners in this examination session.

It is the property of the International Baccalaureate and
must not be reproduced or distributed to any other person
without the authorization of IB Cardiff.

– 3 –

M08/5/MATHL/HP2/ENG/TZ1/XX/M+

Instructions to Examiners

Abbreviations

M

Marks awarded for attempting to use a correct Method; working must be seen.

(M) Marks awarded for Method; may be implied by correct subsequent working.

A

Marks awarded for an Answer or for Accuracy: often dependent on preceding M marks.

(A) Marks awarded for an Answer or for Accuracy; may be implied by correct subsequent working.

R

Marks awarded for clear Reasoning.

N

Marks awarded for correct answers if no working shown.

AG Answer given in the question and so no marks are awarded.

Using the markscheme

1

General

Write the marks in red on candidates’ scripts, in the right hand margin.

• Show the breakdown of individual marks awarded using the abbreviations M1, A1, etc.

• Write down the total for each question (at the end of the question) and circle it.

2

Method and Answer/Accuracy marks

• Do not automatically award full marks for a correct answer; all working must be checked, and

marks awarded according to the markscheme.

• It is not possible to award M0 followed by A1, as A mark(s) depend on the preceding M mark(s), if

any.

• Where M and A marks are noted on the same line, e.g. M1A1, this usually means M1 for an

attempt to use an appropriate method (e.g. substitution into a formula) and A1 for using the
correct values.

• Where the markscheme specifies (M2), N3, etc., do not split the marks.

• Once a correct answer to a question or part-question is seen, ignore further working.

3

N marks

Award

N marks for correct answers where there is no working.

• Do not award a mixture of N and other marks.

• There may be fewer N marks available than the total of M, A and R marks; this is deliberate as it

penalizes candidates for not following the instruction to show their working.

– 4 –

M08/5/MATHL/HP2/ENG/TZ1/XX/M+

4 Implied

marks

Implied marks appear in brackets e.g. (M1), and can only be awarded if correct work is seen or

if

implied in subsequent working.

• Normally the correct work is seen or implied in the next line.

• Marks without brackets can only be awarded for work that is seen.

5 Follow

through

marks

Follow through (FT) marks are awarded where an incorrect answer from one part of a question is
used correctly in subsequent part(s). To award FT marks, there must be working present and not
just a final answer based on an incorrect answer to a previous part.

• If the question becomes much simpler because of an error then use discretion to award fewer FT

marks.

• If the error leads to an inappropriate value (e.g. sin

1.5

θ

=

), do not award the mark(s) for the final

answer(s).

• Within a question part, once an error is made, no further dependent A marks can be awarded, but

M marks may be awarded if appropriate.

• Exceptions to this rule will be explicitly noted on the markscheme.

6

Mis-read

If a candidate incorrectly copies information from the question, this is a mis-read (MR). Apply a MR
penalty of 1 mark to that question. Award the marks as usual and then write –1(MR) next to the total.
Subtract 1 mark from the total for the question. A candidate should be penalized only once for a
particular mis-read.

• If the question becomes much simpler because of the MR, then use discretion to award fewer

marks.

• If the MR leads to an inappropriate value (e.g. sin

1.5

θ

=

), do not award the mark(s) for the final

answer(s).

7

Discretionary marks (d)

An examiner uses discretion to award a mark on the rare occasions when the markscheme does not
cover the work seen. The mark should be labelled (d) and a brief note written next to the mark
explaining this decision.

8

Alternative methods

Candidates will sometimes use methods other than those in the markscheme. Unless the question
specifies a method, other correct methods should be marked in line with the markscheme. If in doubt,
contact your team leader for advice.

• Alternative methods for complete questions are indicated by METHOD 1, METHOD 2, etc.

• Alternative solutions for part-questions are indicated by EITHER . . . OR.

• Where possible, alignment will also be used to assist examiners in identifying where these

alternatives start and finish.

– 5 –

M08/5/MATHL/HP2/ENG/TZ1/XX/M+

9 Alternative

forms

Unless the question specifies otherwise, accept equivalent forms.

• As this is an international examination, accept all alternative forms of notation.

• In the markscheme, equivalent numerical and algebraic forms will generally be written in

brackets immediately following the answer.

• In the markscheme, simplified answers, (which candidates often do not write in examinations), will

generally appear in brackets. Marks should be awarded for either the form preceding the bracket or
the form in brackets (if it is seen).

Example: for differentiating ( ) 2sin (5

3)

f x

x

=

− , the markscheme gives:

(

)

( )

2cos (5

3) 5

f x

x

′

=

−

(

)

10cos (5

3)

x

=

−

A1

Award A1 for

(

)

2cos(5

3) 5

x

−

, even if 10cos (5

3)

x

− is not seen.

10 Accuracy

of

Answers

If the level of accuracy is specified in the question, a mark will be allocated for giving the answer to
the required accuracy.

• Rounding errors: only applies to final answers not to intermediate steps.

• Level of accuracy: when this is not specified in the question the general rule applies: unless

otherwise stated in the question all numerical answers must be given exactly or correct to three
significant figures.

Candidates should be penalized once only IN THE PAPER for an accuracy error (AP). Award the
marks as usual then write (AP) against the answer. On the front cover write –1(AP). Deduct 1 mark
from the total for the paper, not the question.

• If a final correct answer is incorrectly rounded, apply the AP.

• If the level of accuracy is not specified in the question, apply the AP for correct answers not given

to three significant figures.

If there is no working shown, and answers are given to the correct two significant figures, apply the
AP. However, do not accept answers to one significant figure without working.

11

Crossed out work

If a candidate has drawn a line through work on their examination script, or in some other way
crossed out their work, do not award any marks for that work.

– 6 –

M08/5/MATHL/HP2/ENG/TZ1/XX/M+

SECTION A

1. METHOD

1

constant term:

0

0

5

7

( 2 )

1

0

0

x

x

⎛ ⎞

⎛ ⎞

−

=

⎜ ⎟

⎜ ⎟

⎝ ⎠

⎝ ⎠

A1

term

in

x:

7

5

( 2 )

3

1

1

x

x

x

⎛ ⎞

⎛ ⎞

+

−

= −

⎜ ⎟

⎜ ⎟

⎝ ⎠

⎝ ⎠

(M1)A1

term

in

2

x

:

2

2

2

7

5

7

5

( 2 )

( 2 )

9

2

2

1

1

x

x

x

x

x

⎛ ⎞

⎛ ⎞

⎛ ⎞ ⎛ ⎞

+

−

+

−

= −

⎜ ⎟

⎜ ⎟

⎜ ⎟ ⎜ ⎟

⎝ ⎠

⎝ ⎠

⎝ ⎠ ⎝ ⎠

M1A1 N3

[5 marks]

METHOD

2

2

5

7

2

5 4( 2 )

7 6

(1 2 ) (1

)

1 5( 2 )

... 1 7

...

2!

2

x

x

x

x

x

x

⎛

⎞

× −

×

⎛

⎞

−

+

= + −

+

+

+

+

+

⎜

⎟⎜

⎟

⎝

⎠

⎝

⎠

M1M1

2

2

(1 10

40

...)(1 7

21

...)

x

x

x

x

= −

+

+

+

+

+

2

2

2

1 7

21

10

70

40

...

x

x

x

x

x

= +

+

−

−

+

+

2

1 3

9

...

x

x

= −

−

+

A1A1A1 N3

[5 marks]

– 7 –

M08/5/MATHL/HP2/ENG/TZ1/XX/M+

2. (a)

A1A1A1A1

Note: Award A1 for y-intercept

A1A1 for x-intercepts

A1 for shape

(b) correct

line

A1

5

solutions

A1

[6 marks]

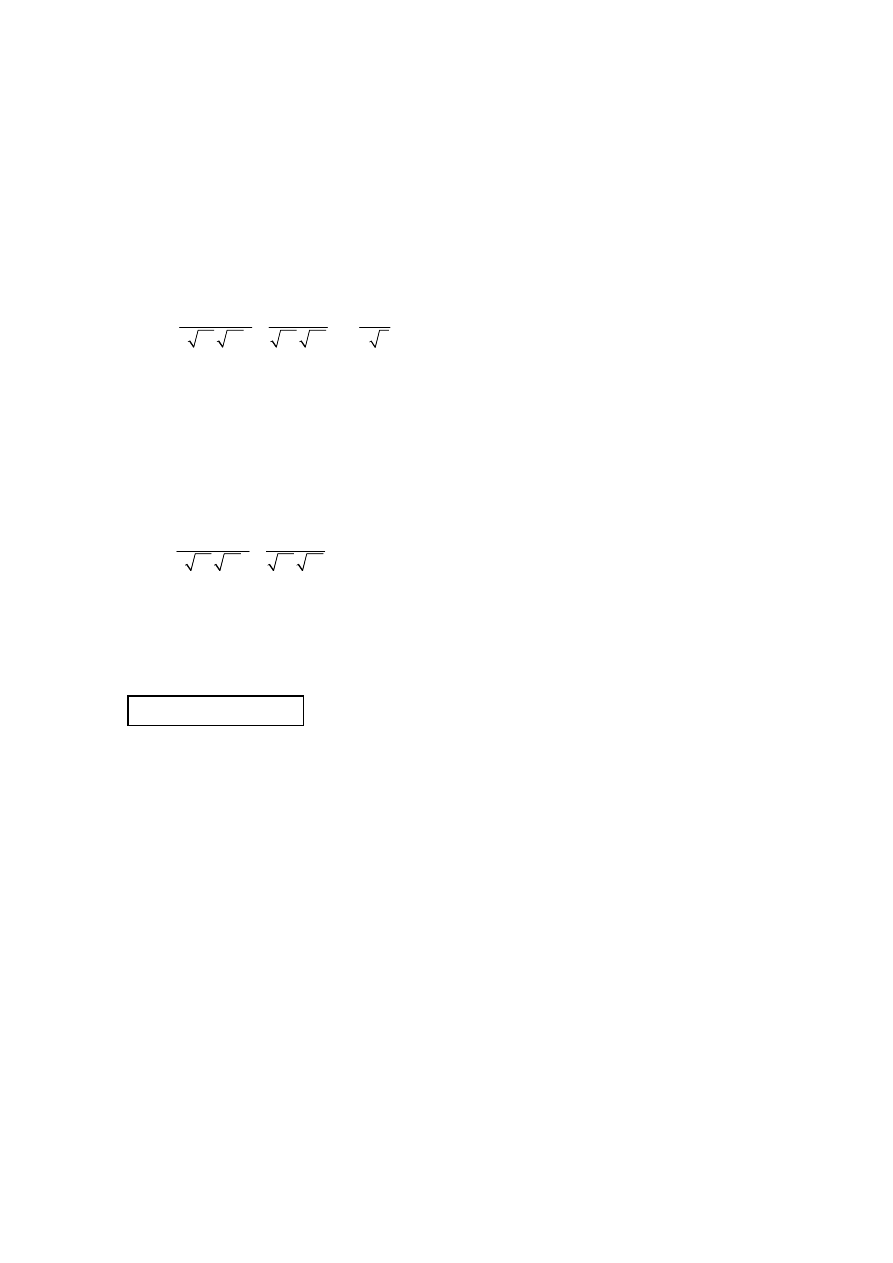
– 8 –

M08/5/MATHL/HP2/ENG/TZ1/XX/M+

3.

The normal vector to the plane is

1
3
2

⎛ ⎞

⎜ ⎟

⎜ ⎟

⎜ ⎟

⎝ ⎠

.

(A1)

EITHER

θ

is the angle between the line and the normal to the plane.

4

1

1

3

2

2

3

3

cos

14 21

14 21

7 6

θ

⎛

⎞ ⎛ ⎞

⎜

⎟ ⎜ ⎟

•

⎜

⎟ ⎜ ⎟

⎜

⎟ ⎜ ⎟

−

⎛

⎞

⎝

⎠ ⎝ ⎠

=

=

=

⎜

⎟

⎝

⎠

(M1)A1A1

79.9 ( 1.394...)

θ

⇒ =

=

D

A1

The required angle is 10.1 ( 0.176)

=

D

A1

OR

φ

is the angle between the line and the plane.

4

1

1

3

2

2

3

sin

14 21

14 21

φ

⎛

⎞ ⎛ ⎞

⎜

⎟ ⎜ ⎟

•

⎜

⎟ ⎜ ⎟

⎜

⎟ ⎜ ⎟

−

⎝

⎠ ⎝ ⎠

=

=

(M1)A1A1

10.1 ( 0.176)

φ

=

=

D

A2

[6 marks]

4. (a) P (

84) P(

1.62...) 0.0524

X

Z

≤

=

≤ −

=

(M1)A1

N2

Note: Accept 0.0526.

(b)

P (

) 0.01

2.326...

Z

z

z

≤

=

⇒ = −

(M1)

P (

) P(

) 0.01

2.326...

X

x

Z

z

z

≤

=

≤

=

⇒ = −

81.4

x

=

(accept 81)

A1 N2

(c)

P (

84) 0.12

1.1749...

X

z

≤

=

⇒ = −

(M1)

mean is 88.3 (accept 88)

A1 N2

[6 marks]

– 9 –

M08/5/MATHL/HP2/ENG/TZ1/XX/M+

5.

METHOD 1

(from GDC)

1

1

1 0

6

12

2

1

0 1

3

6

0 0

0

0

⎛

⎞

−

⎜

⎟

⎜

⎟

⎜

⎟

−

−

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎝

⎠

(M1)

1

1

6

12

x

λ

+

= −

A1

2

1

3

6

y

λ

−

= −

A1

1

1

1

2

12

6

6

3

λ

⎛

⎞

⎛

⎞

= −

−

+

−

+

+

⎜

⎟

⎜

⎟

⎝

⎠

⎝

⎠

r

i

j

i

j k

A1A1A1 N3

[6 marks]

METHOD 2

(Elimination method either for equations or row reduction of matrix)

Eliminating one of the variables

M1A1

Finding a point on the line (M1)A1

Finding the direction of the line

M1

The

vector equation of the line

A1 N3

[6 marks]

– 10 –

M08/5/MATHL/HP2/ENG/TZ1/XX/M+

6.

METHOD 1

2

2

3

d

d

3

2

sin ( )

d

d

y

y

x y

x y

y

x

x

+

= −π

π

A1A1A1

At

( 1, 1)

−

,

d

3 2

0

d

y
x

−

=

M1A1

d

3

d

2

y
x

=

A1

[6 marks]

METHOD

2

2

2

3

d

d

3

2

sin ( )

d

d

y

y

x y

x y

y

x

x

+

= −π

π

A1A1A1

2

2

3

d

3

d

sin ( ) 2

y

x y

x

y

x y

=

−π

π −

A1

2

2

3

d

3( 1) (1)

3

At ( 1, 1),

d

sin ( ) 2( 1) (1)

2

y
x

−

−

=

=

−π

π − −

M1A1

[6 marks]

7. (a)

arccos(1.2 cos )

y

x

=

−

A1

arcsin (1.4 sin )

y

x

=

−

A1

(b)

The solutions are

1.26,

0.464

x

y

=

=

A1A1

0.464,

1.26

x

y

=

=

A1A1

[6 marks]

– 11 –

M08/5/MATHL/HP2/ENG/TZ1/XX/M+

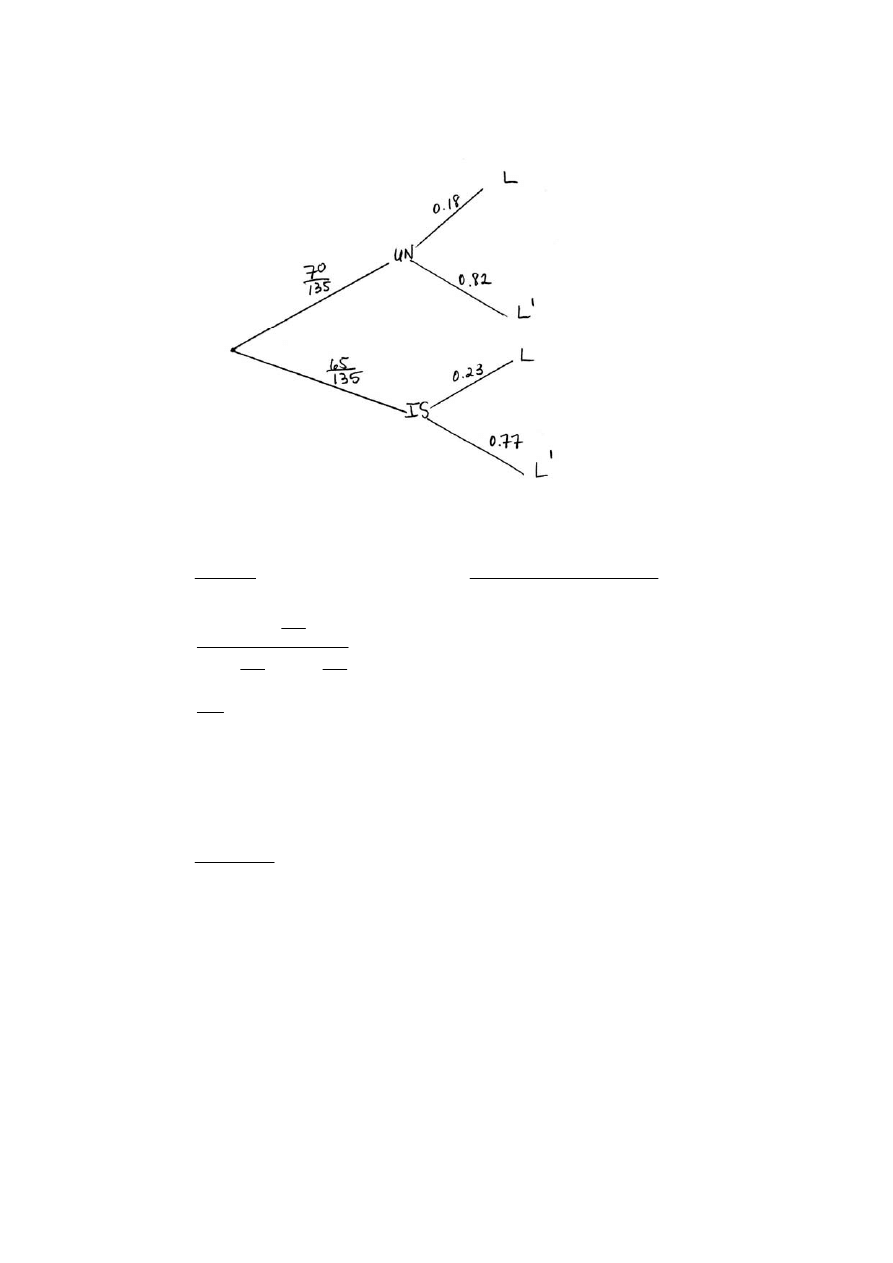
8. METHOD

1

(M1)

Let P ( )

I

be the probability of flying IS Air, P ( )

U

be the probability flying UN Air

and P ( )

L

be the probability of luggage lost.

P(

)

P ( | ) P ( )

P ( | )

or Bayes' formula , P ( | )

P( )

P( | ) P( ) P( | ) P( )

I

L

L I

I

I L

I L

L

L I

I

L U

U

⎛

⎞

∩

=

=

⎜

⎟

+

⎝

⎠

(M1)

65

0.23

135

70

65

0.18

0.23

135

135

×

=

×

+

×

A1A1A1

299

( 0.543, accept 0.542)

551

=

=

A1

[6 marks]

METHOD 2

Expected number of suitcases lost by UN Air is 0.18 70 12.6

×

=

M1A1

Expected number of suitcases lost by IS Air is 0.23 65 14.95

×

=

A1

14.95

P ( | )

12.6 14.95

I L

=

+

M1A1

0.543

=

A1

[6 marks]

– 12 –

M08/5/MATHL/HP2/ENG/TZ1/XX/M+

9. Let

1

ln

d

d

u

y

u

y

y

=

⇒

=

A1(A1)

tan (ln )

d

tan d

y

y

u u

y

=

∫

∫

A1

sin

d

ln cos

cos

u

u

u

c

u

=

= −

+

∫

A1

EITHER

tan (ln )

d

ln cos(ln )

y

y

y

c

y

= −

+

∫

A1A1

OR

tan (ln )

d

ln sec(ln )

y

y

y

c

y

=

+

∫

A1A1

[6 marks]

10.

(

)

2

2

2

sin

i (1 cos )

sin

(1 cos )

i 2sin (1 cos )

θ

θ

θ

θ

θ

θ

+

−

=

− −

+

−

M1A1

Let

α

be the required argument.

2

2

2sin (1 cos )

tan

sin

(1 cos )

θ

θ

α

θ

θ

−

=

− −

M1

2

2

2sin (1 cos )

(1 cos

) (1 2cos

cos

)

θ

θ

θ

θ

θ

−

=

−

− −

+

(M1)

2sin (1 cos )

2cos (1 cos )

θ

θ

θ

θ

−

=

−

A1

tan

θ

=

A1

α θ

=

A1

[7 marks]

– 13 –

M08/5/MATHL/HP2/ENG/TZ1/XX/M+

SECTION B

11. (a)

mean for 30 days: 30 0.2 6

×

= .

(A1)

4

6

6

P (

4)

e

0.134

4!

X

−

=

=

=

(M1)A1 N3

[3 marks]

(b)

6

P (

3) 1 P(

3) 1 e (1 6 18 36) 0.849

X

X

−

> = −

≤ = −

+ +

+

=

(M1)A1 N2

[2 marks]

(c)

EITHER

mean for five days: 5 0.2 1

×

=

(A1)

1

P (

0) e

( 0.368)

X

−

=

=

=

A1 N2

OR

mean for one day: 0.2

(A1)

0.2 5

1

P (

0) (e

)

e

( 0.368)

X

−

−

=

=

=

=

A1 N2

[2 marks]

(d)

Required

probability

0.2

0.2

0.2

e

e

(1 e

)

−

−

−

=

×

× −

M1A1

0.122

=

A1 N3

[3 marks]

(e) Expected cost is 1850 6 11100

× =

Euros

A1

[1 mark]

(f)

On any one day

0.2

P (

0) e

X

−

=

=

Therefore,

0.2 4

0.2

5

(e

) (1 e

) 0.407

1

−

−

⎛ ⎞

−

=

⎜ ⎟

⎝ ⎠

M1A1 N2

[2 marks]

Total [13 marks]

– 14 –

M08/5/MATHL/HP2/ENG/TZ1/XX/M+

12. Part A

(a)

CD AC AD

cos

b c

A

=

−

= −

R1AG

[1 mark]

(b)

METHOD 1

2

2

2

BC

BD

CD

=

+

(M1)

2

2

2

( sin )

(

cos )

a

c

A

b c

A

=

+ −

(A1)

2

2

2

2

2

sin

2 cos

cos

c

A b

bc

A c

A

=

+

−

+

A1

2

2

2 cos

b

c

bc

A

=

+

−

A1

[4 marks]

METHOD 2

2

2

2

2

2

BD

AB

AD

BC

CD

=

−

=

−

(M1)(A1)

2

2

2

2

2

2

2

cos

2 cos

cos

c

c

A a

b

bc

A c

A

⇒

−

=

−

+

−

A1

2

2

2

2 cos

a

b

c

bc

A

⇒

=

+

−

A1

[4 marks]

(c)

METHOD 1

2

2

2

2

2

2

2 cos 60

b

a

c

ac

b

a

c

ac

=

+

−

⇒

=

+

−

D

(M1)A1

2

2

2

0

c

ac a

b

⇒

−

+

−

=

M1

2

2

2

(

)

4(

)

2

a

a

a

b

c

±

−

−

−

⇒ =

(M1)A1

2

2

2

2

4

3

4

3

2

2

4

a

b

a

a

b

a

±

−

−

=

= ±

(M1)A1

2

2

1

3

2

4

a

b

a

=

±

−

AG

Note: Candidates can only obtain a maximum of the first three marks if they

verify that the answer given in the question satisfies the equation.

[7 marks]

METHOD

2

2

2

2

2

2

2

2 cos 60

b

a

c

ac

b

a

c

ac

=

+

−

⇒

=

+

−

D

(M1)A1

2

2

2

c

ac b

a

−

=

−

(M1)

2

2

2

2

2

2

2

a

a

c

ac

b

a

⎛ ⎞

⎛ ⎞

−

+

=

−

+

⎜ ⎟

⎜ ⎟

⎝ ⎠

⎝ ⎠

M1A1

2

2

2

3

2

4

a

c

b

a

⎛

⎞

−

=

−

⎜

⎟

⎝

⎠

(A1)

2

2

3

2

4

a

c

b

a

− = ±

−

A1

2

2

1

3

2

4

c

a

b

a

⇒ =

±

−

AG

[7 marks]

Sub-Total [12 marks]

continued

…

– 15 –

M08/5/MATHL/HP2/ENG/TZ1/XX/M+

Question 12 continued

Part

B

PR

tan 55 , QR

tan 50 where RS

h

h

h

=

=

=

D

D

M1A1A1

Use the cosine rule in triangle PQR.

(M1)

2

2

2

2

2

20

tan 55

tan 50

2 tan 55 tan 50 cos 45

h

h

h

h

=

+

−

D

D

D

D

D

A1

2

2

2

400

tan 55

tan 50

2 tan 55 tan 50 cos 45

h

=

+

−

D

D

D

D

D

(A1)

379.9...

=

(A1)

19.5 (m)

h

=

A1

[8 marks]

Total [20 marks]

13. (a) (i)

2 2

( ) 3

2

1

k

f x

k x

kx

′

=

−

+

A1

2

( ) 6

2

k

f x

k x

k

′′

=

−

A1

(ii)

Setting

( ) 0

f x

′′

=

M1

2

1

6

2

0

3

k x

k

x

k

⇒

−

= ⇒ =

A1

3

2

2

1

1

1

1

3

3

3

3

f

k

k

k

k

k

k

⎛

⎞

⎛

⎞

⎛

⎞

⎛

⎞

=

−

+

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎝

⎠

⎝

⎠

⎝

⎠

⎝

⎠

M1

7

27k

=

A1

Hence,

1

7

is

,

3

27

k

P

k

k

⎛

⎞

⎜

⎟

⎝

⎠

[6 marks]

(b)

Equation of the straight line is

7
9

y

x

=

A1

As this equation is independent of k, all

k

P

lie on this straight line

R1

[2 marks]

(c)

Gradient of tangent at

k

P

:

2

2

1

1

1

2

( )

3

2

1

3

3

3

3

k

f P

f

k

k

k

k

k

⎛

⎞

⎛

⎞

⎛

⎞

′

′

=

=

−

+ =

⎜

⎟

⎜

⎟

⎜

⎟

⎝

⎠

⎝

⎠

⎝

⎠

M1A1

As the gradient is independent of k, the tangents are parallel.

R1

7

2

1

1

27

3 3

27

c

c

k

k

k

= ×

+ ⇒ =

(A1)

The

equation

is

2

1

3

27

y

x

k

=

+

A1

[5 marks]

Total [13 marks]

– 16 –

M08/5/MATHL/HP2/ENG/TZ1/XX/M+

14. (a)

1 i 3

2

+

= or 1 i

2

− =

(A1)

arg (1 i 3)

3

π

+

= or arg (1 i)

4

π

− = −

7

accept

4

π

⎛

⎞

⎜

⎟

⎝

⎠

(A1)

1

2

m

z

=

A1

2

2

n

z

=

A1

1

arg ( )

arctan 3

3

z

m

m

π

=

=

A1

2

arg ( )

arctan ( 1)

4

z

n

n

−π

=

− =

7

accept

4

n

π

⎛

⎞

⎜

⎟

⎝

⎠

A1 N2

[6 marks]

(b)

2

2

2

n

m

n

m

=

⇒ =

(M1)A1

2

3

4

m

n

k

π

−π

=

+ π , where k is an integer

M1A1

2

3

4

m

n

k

π

π

⇒

+

= π

2

2

3

4

m

m

k

π

π

⇒

+

= π

(M1)

5

π 2π

6

m

k

=

12

5

m

k

⇒ =

A1

The smallest value of k such that m is an integer is 5, hence

12

m

=

A1

24

n

=

.

A1

N2

[8 marks]

Total [14 marks]