1

Dynamika
ruchu kulistego

Ćwiczenia 13

dr inż. Monika Kwacz

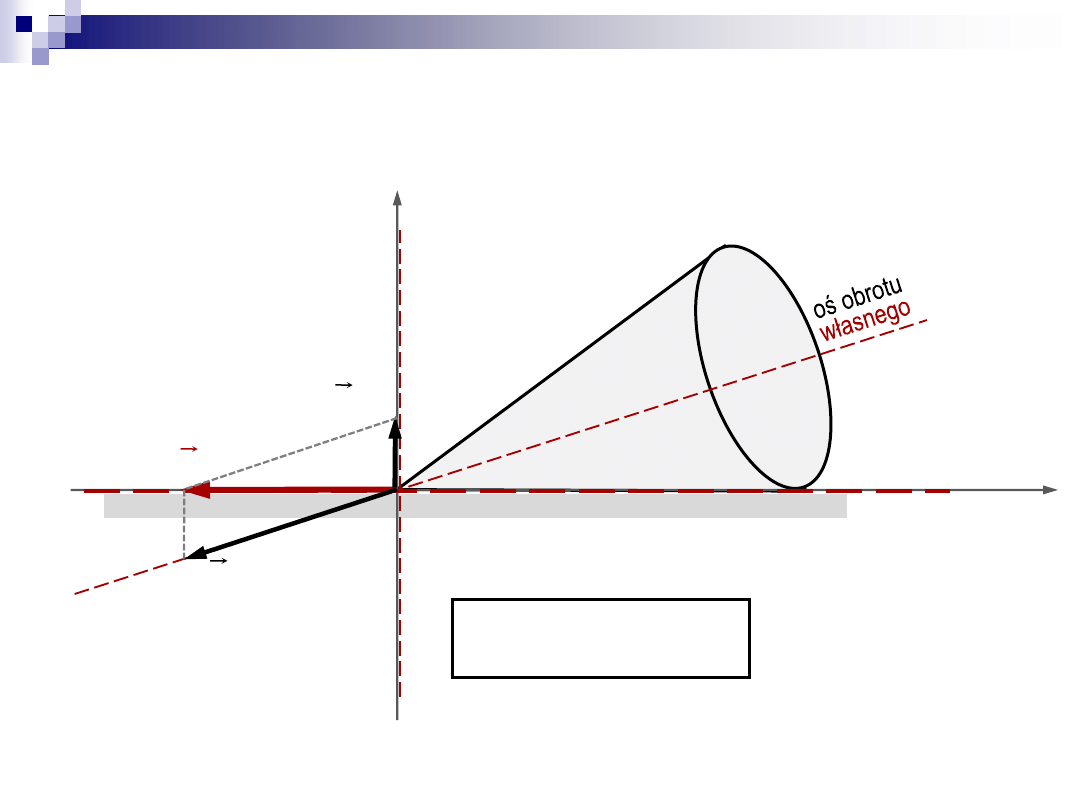
Ruch kulisty – kinematyka

Wstęp

w

w

wł

w

prec

wł

prec

w

w

w











oś

pre

cesji

chwilowa

oś obrotu

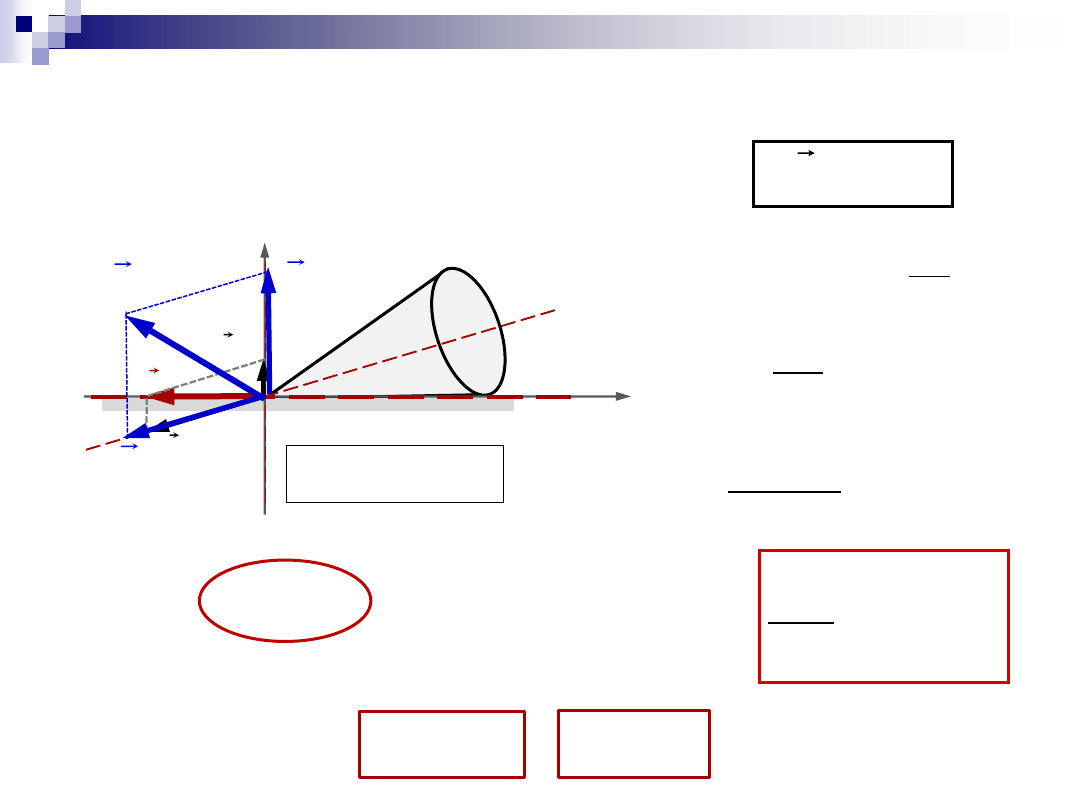
Ruch kulisty – dynamika

Wstęp

zew

M

I











uwzględniając:

dt

d

w









zew

M

dt

d

I











w

oznaczając:

w









I

K

kręt





zew

M

dt

I

d











w

zew

M

dt

K

d









w

w

wł

w

prec

Dynamiczne równanie ruchu obrotowego:

przy czym:



K



wł

prec

w

w

w











K

1

K

2

K

prec

prec

I

w





wł

wł

I

w





2

1

K

K











otrzymujemy:

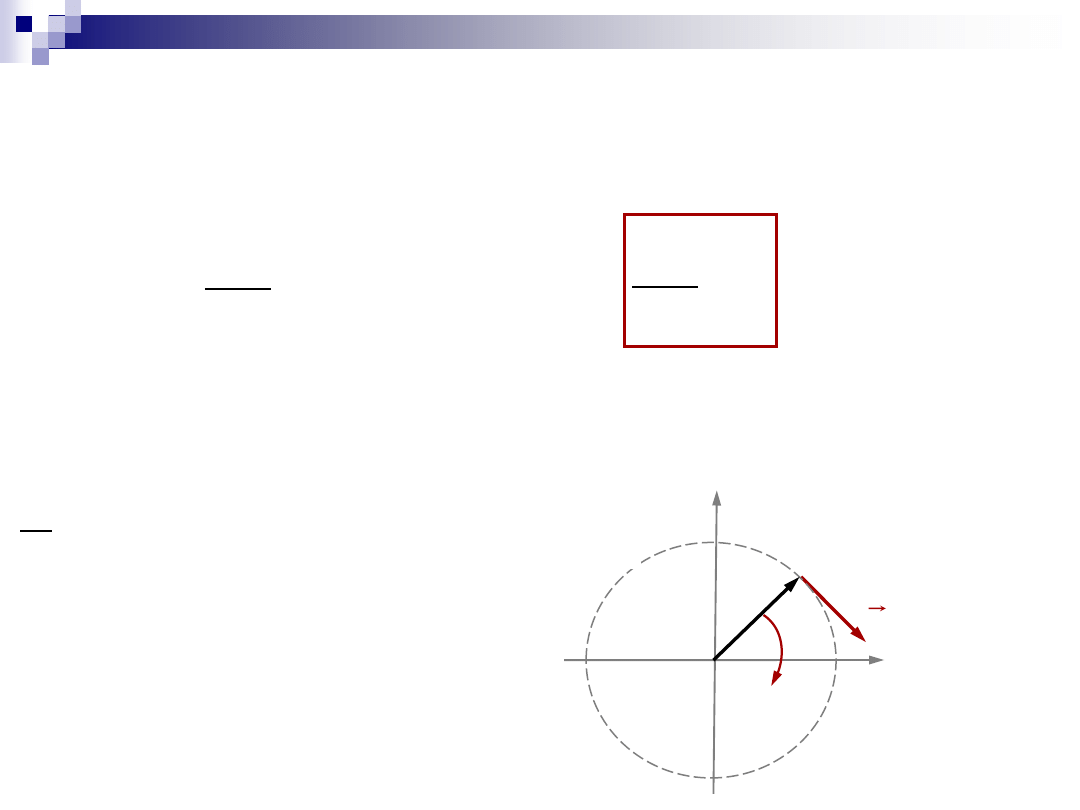
Kinematyczna interpretacja

pochodnej wektora

Wstęp

zew

M

dt

K

d









pochodna wektora =

prędkości liniowej

z jaką porusza się koniec wektora

u





u

w

w

w

w























































r

r

r

k

j

i

r

r

dt

d

r

dt

d

r

dt

r

r

d

dt

r

d

y

x

x

y

0

0

0

,

cos

,

sin

]

sin

,

cos

[

r



w

x

y

?



dt

K

d



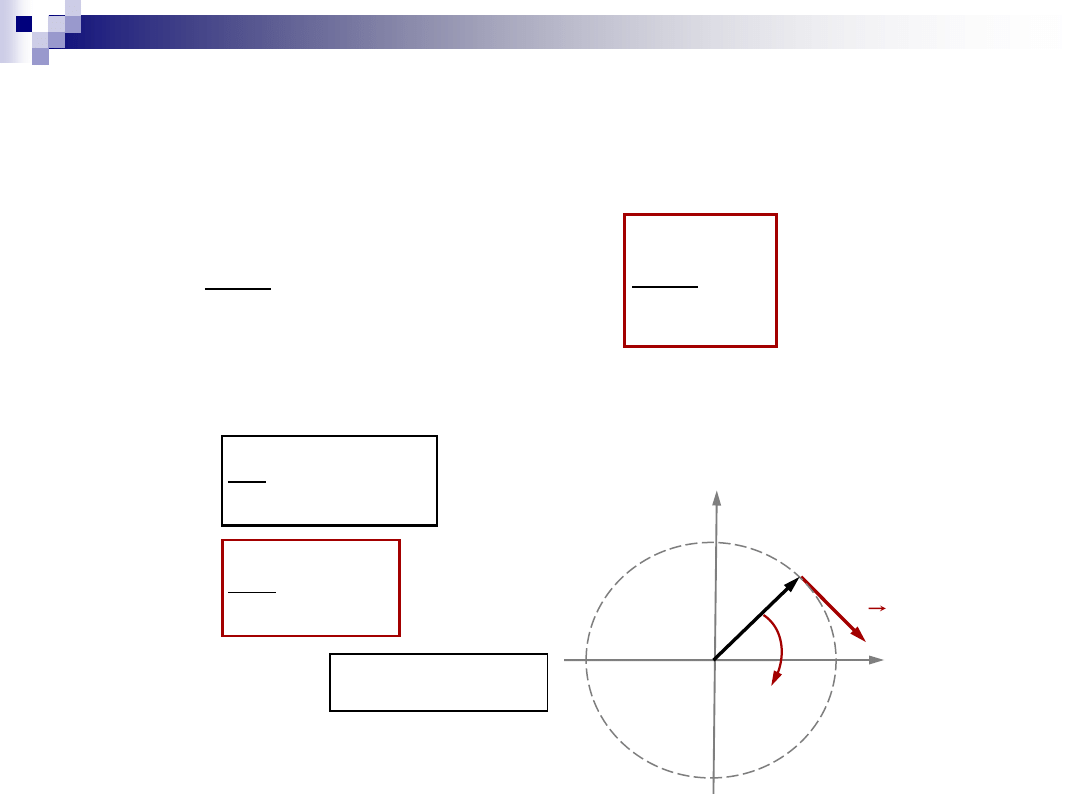
Kinematyczna interpretacja

pochodnej wektora

Wstęp

pochodna wektora =

prędkości liniowej

z jaką porusza się koniec wektora

u

r



w

x

y

r

dt

r

d















w

u

zew

M

dt

K

d









K

dt

K

d











w

?



dt

K

d



wł

prec

w

w

w











w ruchu kulistym:

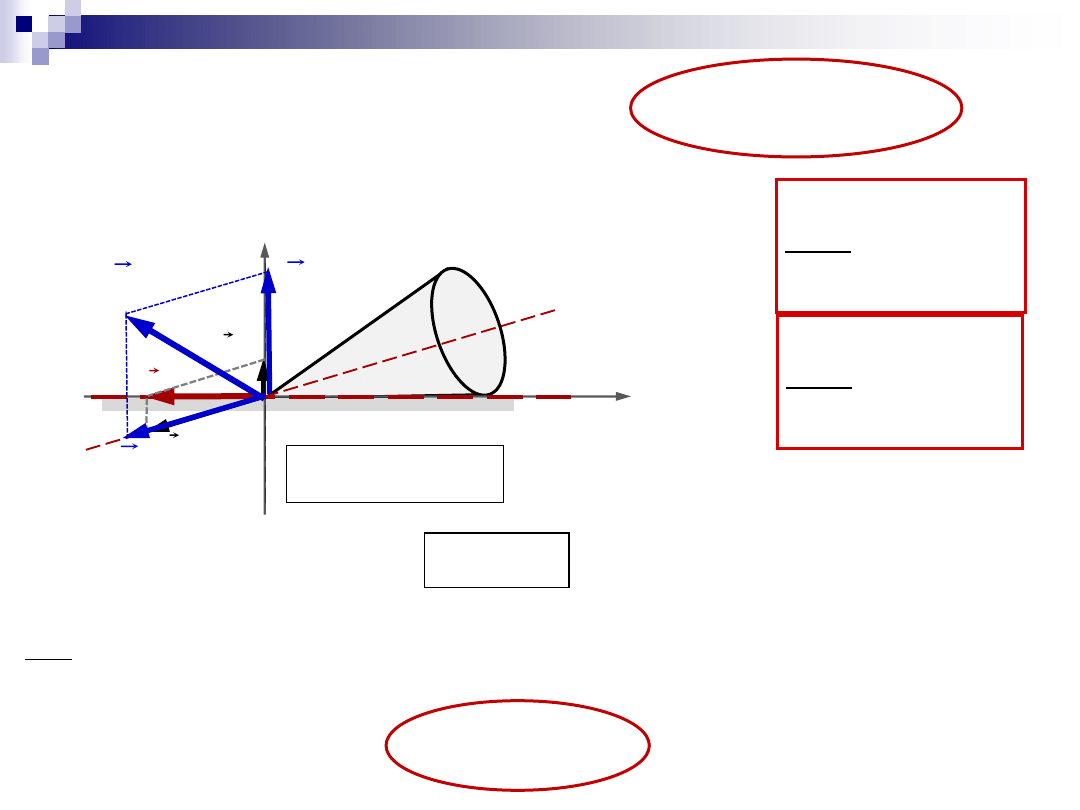
Wstęp

zew

M

dt

K

d









w

w

wł

w

prec

K

1

K

2

K

wł

prec

w

w

w











wł

wł

prec

prec

I

I

K

w

w















wł

wł

I

w













K

dt

K

d







w

K

dt

K

d











w













wł

wł

wł

prec

I

w

w

w



















wł

wł

wł

wł

wł

prec

I

I

w

w

w

w



















0

wł

wł

prec

I

w

w









wł

prec

wł

I

w

w









Ruch kulisty dla

w

wł

»

w

prec

(żyroskop)

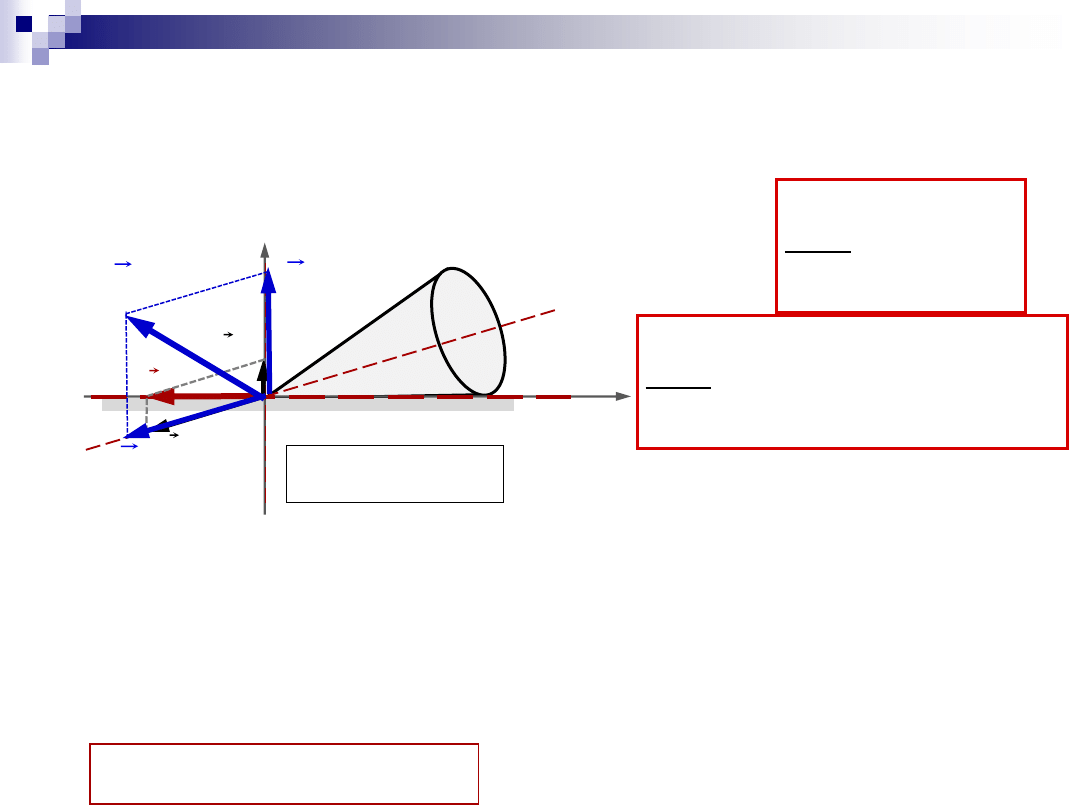
Ruch kulisty dla

w

wł

»

w

prec

(żyroskop)

Wstęp

zew

M

dt

K

d









w

w

wł

w

prec

K

1

K

2

K

wł

prec

w

w

w















wł

prec

wł

I

dt

K

d

w

w













1. z równoległoboku prędkości →

w

wł

2. obliczyć



)

(O

zew

M

(suma momentów sił zewnętrznych np. wzgl. środka ruchu kulistego)

3. obliczyć

wł

I

(moment bezwładności wzgl. osi obrotu własnego)

4. obliczyć





wł

prec

wł

I

w

w









5.













)

(O

zew

wł

prec

wł

M

I

w

w





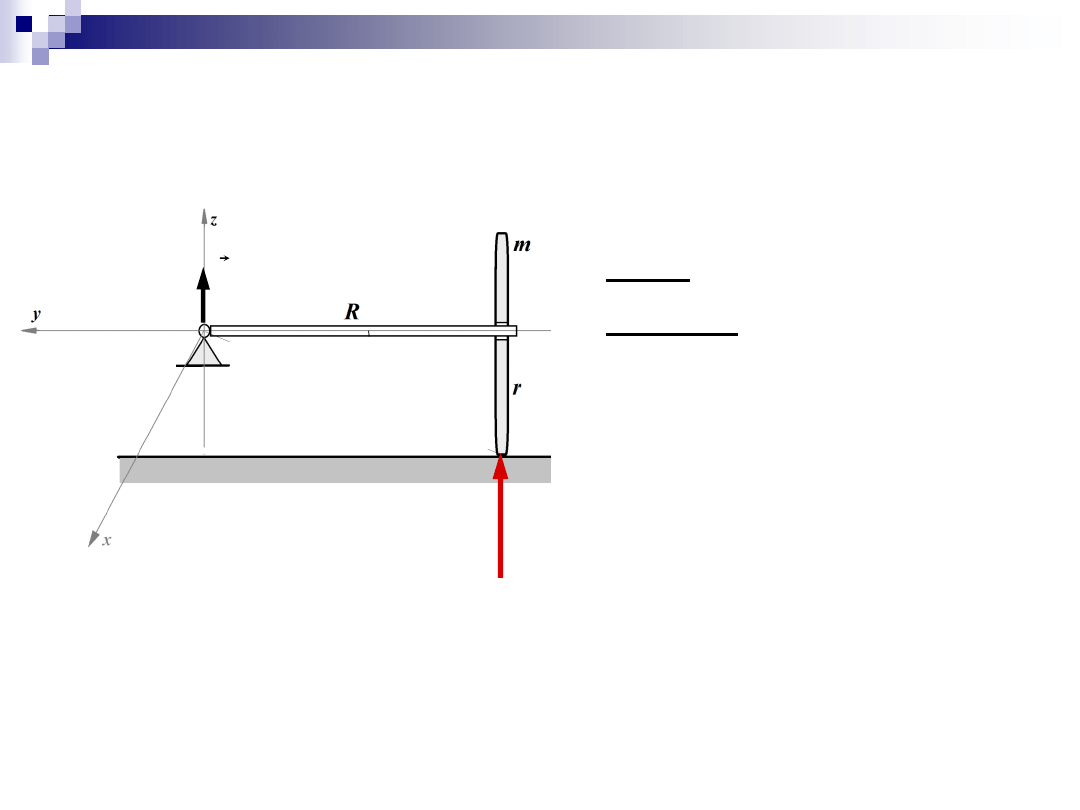
Zadanie 1

Dane: m, r, R,

w

prec

Szukane:

N

– nacisk koła na podłoże

Zadanie 1

N

w

prec

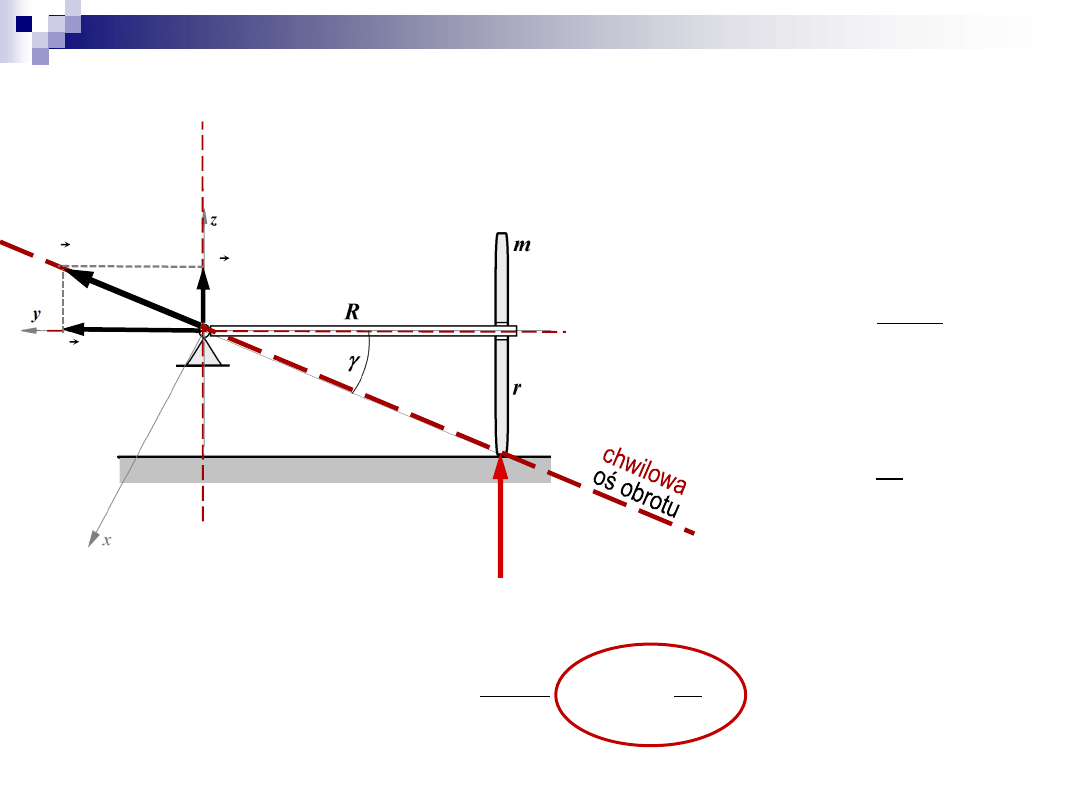
Zadanie 1

N

oś

pre

cesji

O

oś obrotu

własnego

w

prec

w

wł

w

1. Wyznaczenie

w

wł

1. z równoległoboku prędkości →

w

wł

wł

prec

tg

w

w





R

r

tg





r

R

tg

prec

prec

wł







w



w

w

przy czym:

zatem:

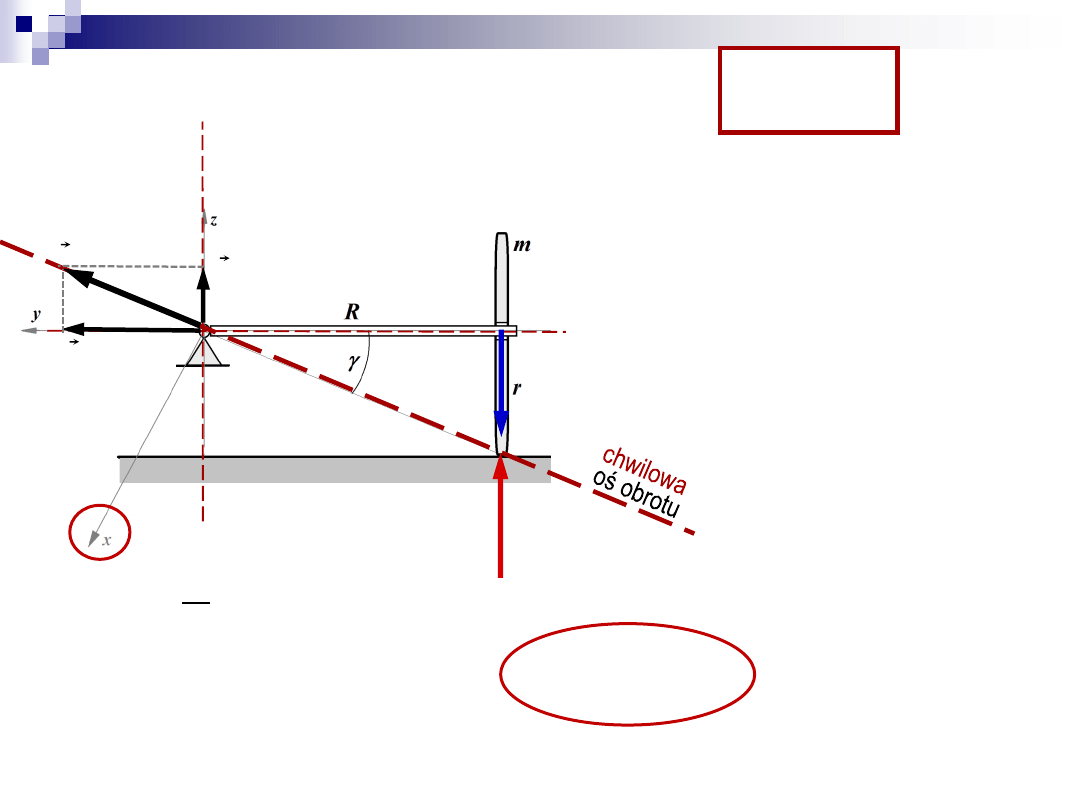
Zadanie 1

N

oś

pre

cesji

O

oś obrotu

własnego

w

prec

w

wł

w

2. Obliczenie

1. z równoległoboku prędkości →

w

wł

r

R

prec

wł





w

w



)

(O

zew

M

2. obliczyć



)

(O

zew

M

(suma momentów sił zewn.
względem osi

x

)

mg

R

mg

R

N

M

O

zew











)

(

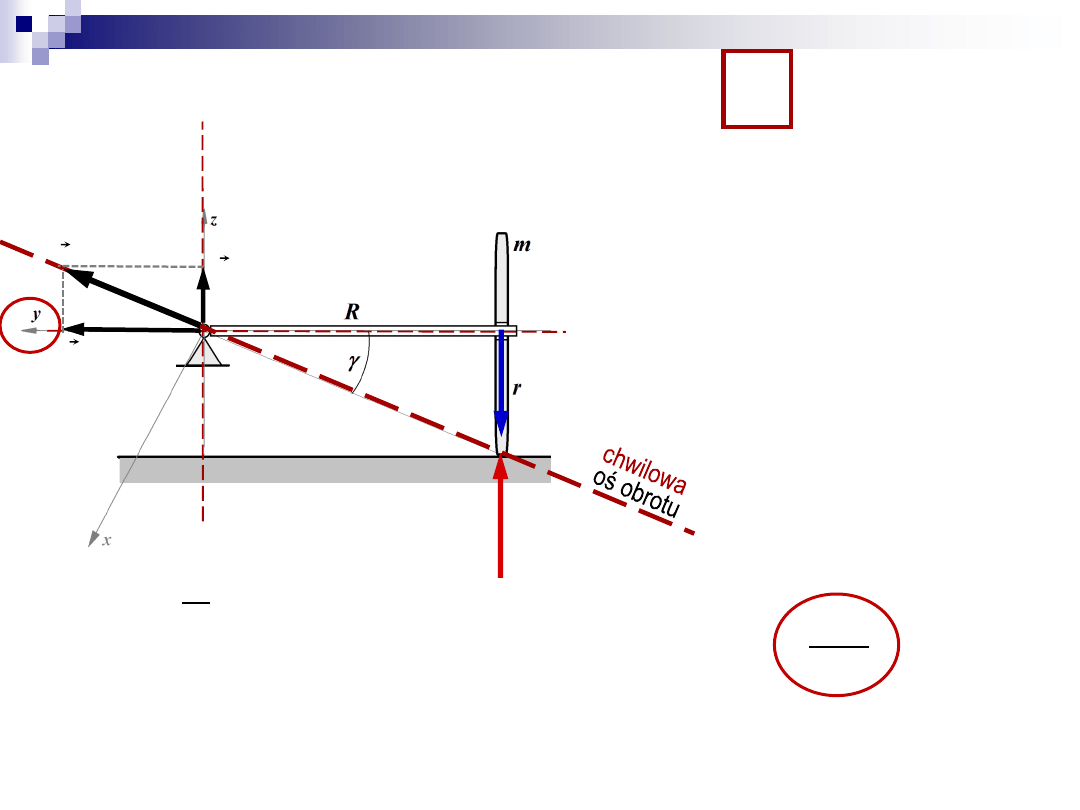
Zadanie 1

N

oś

pre

cesji

O

oś obrotu

własnego

w

prec

w

wł

w

3. Obliczenie

1. z równoległoboku prędkości →

w

wł

r

R

prec

wł





w

w

wł

I

2. obliczyć



)

(O

zew

M

(suma momentów sił zewn.
względem osi

x

)

mg

R

mg

R

N

M

O

zew











)

(

3. obliczyć

wł

I

(moment bezwładności
względem osi obr. własnego y)

2

2

mr

I

I

wł

y





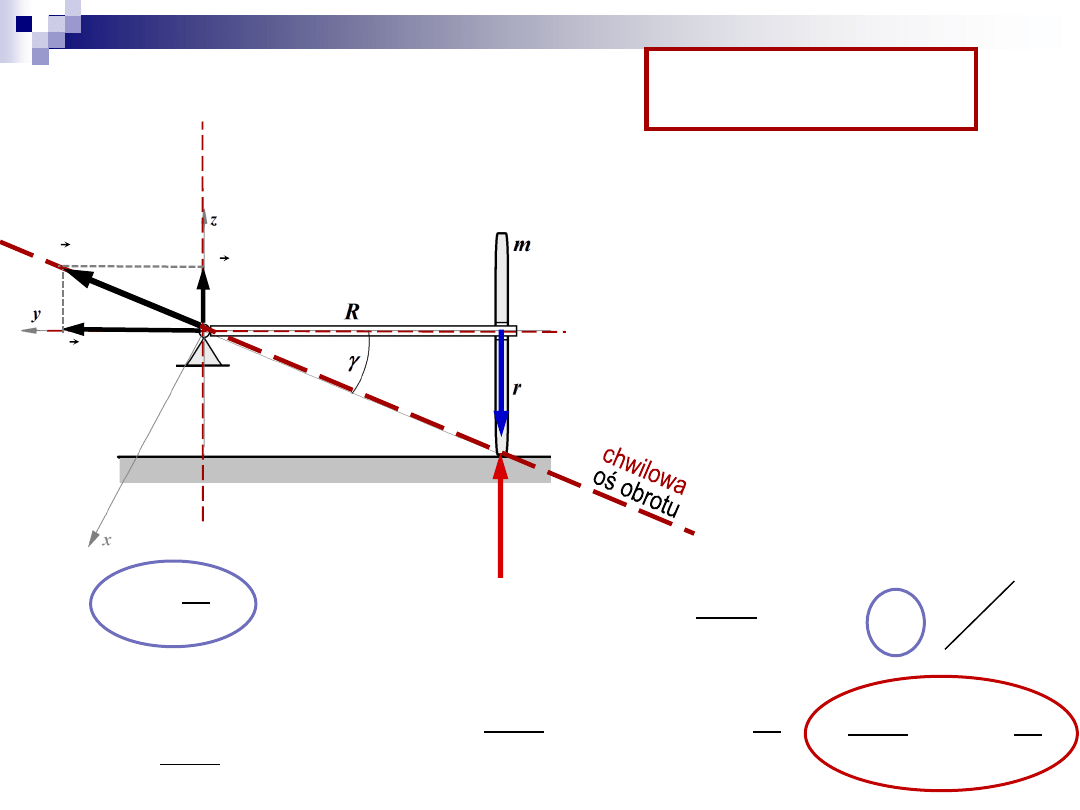
Zadanie 1

N

oś

pre

cesji

O

oś obrotu

własnego

w

prec

w

wł

w

4. Obliczenie

1. z równoległoboku prędkości →

w

wł

r

R

prec

wł





w

w





wł

prec

wł

I

w

w









2. obliczyć



)

(O

zew

M

(suma momentów sił zewn.
względem osi

x

)

mg

R

mg

R

N

M

O

zew











)

(

3. obliczyć

wł

I

(moment bezwładności
względem osi obr. własnego y)

2

2

mr

I

I

wł

y





4. obliczyć





wł

prec

wł

I

w

w



















wł

prec

wł

I

w

w



















90

sin

2

2

wł

prec

mr

w

w























r

R

mr

prec

prec

w

w

2

2

r

R

mr

prec





2

2

2

w

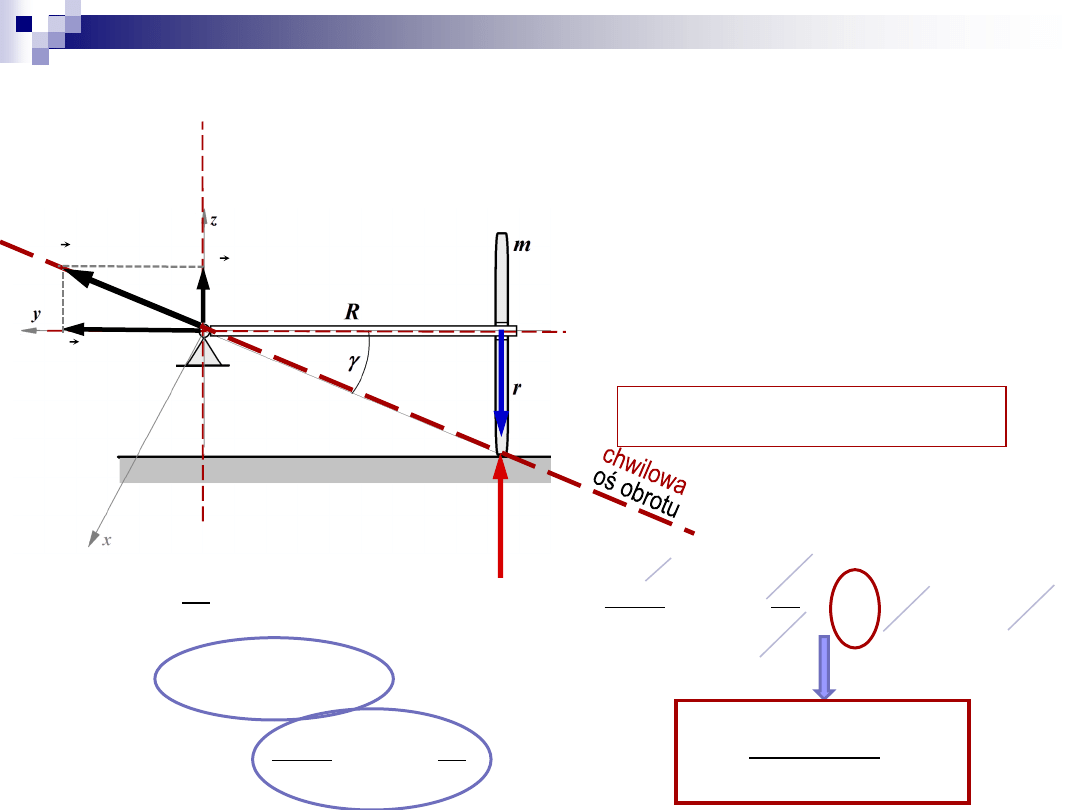
Zadanie 1

N

oś

pre

cesji

O

oś obrotu

własnego

w

prec

w

wł

w

5. Obliczenie

N

1. z równoległoboku prędkości →

w

wł

r

R

prec

wł





w

w

2. obliczyć



)

(O

zew

M

(suma momentów sił zewn.
względem osi

x

)

mg

R

mg

R

N

M

O

zew











)

(

3. obliczyć

wł

I

(moment bezwładności
względem osi obr. własnego y)

4. obliczyć





wł

prec

wł

I

w

w













r

R

mr

I

prec

wł

prec

wł











2

2

2

w

w

w





5.













)

(O

zew

wł

prec

wł

M

I

w

w





czyli:







r

R

mr

prec

2

2

2

w

R

mg

R

N







mg

mr

N

prec







2

2

w

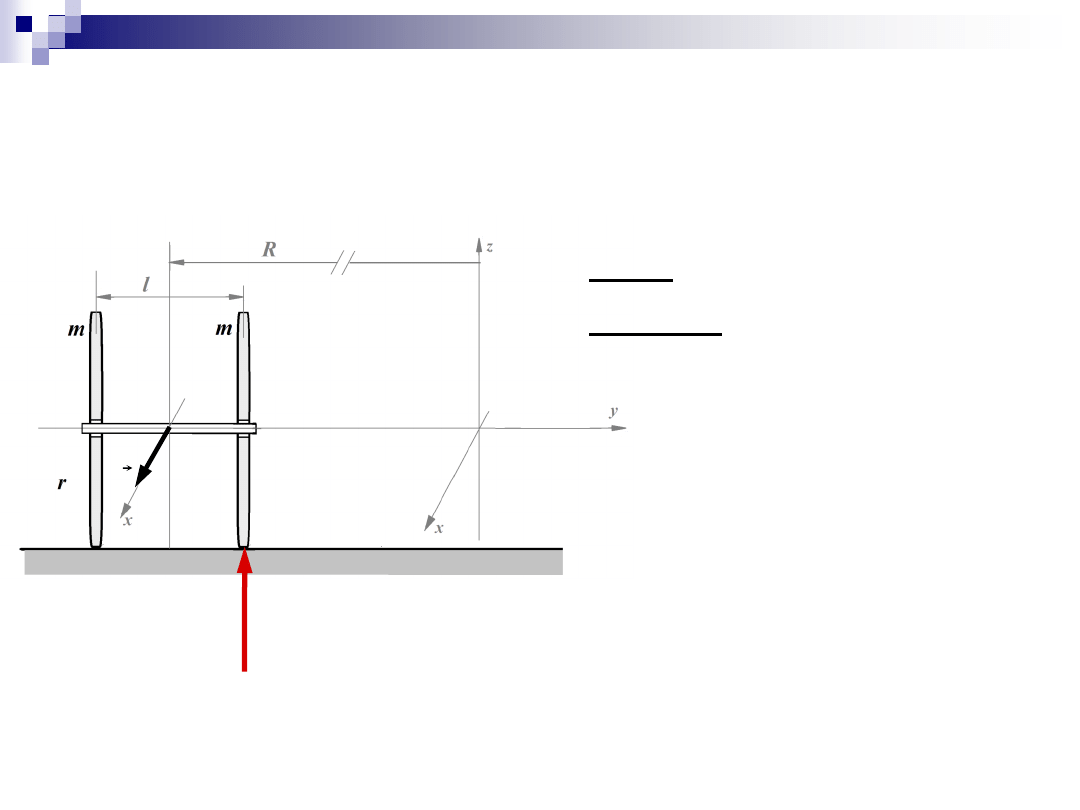
Zadanie 2

Dane: m, r, R, l,

u

Szukane:

N

D

– nacisk koła na podłoże

Zadanie 2

N

D

u

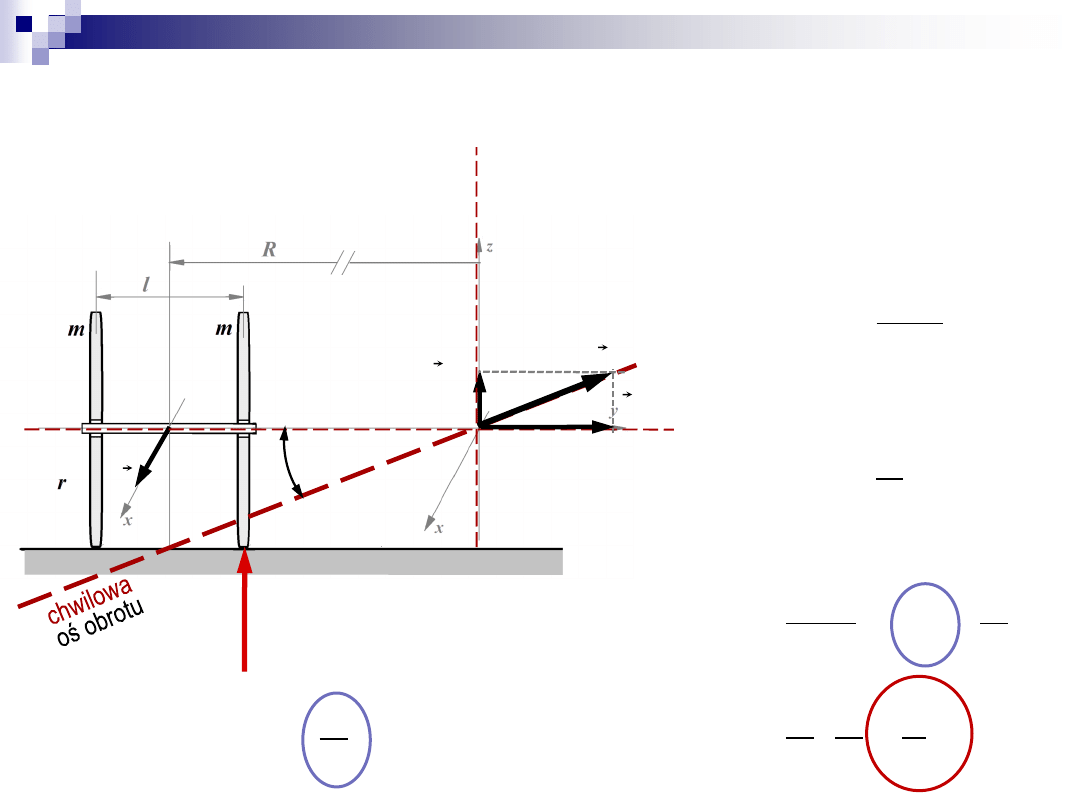
Zadanie 2

N

D

w

prec

u

1. Wyznaczenie

w

wł

1. z równoległoboku prędkości →

w

wł

oś

pre

cesji

oś obrotu

własnego

O

w

wł

w



wł

prec

tg

w

w





R

r

tg





r

R

tg

prec

prec

wł







w



w

w

przy czym:

więc:

gdzie:

R

prec

u

w



r

r

R

R

wł

u

u

w







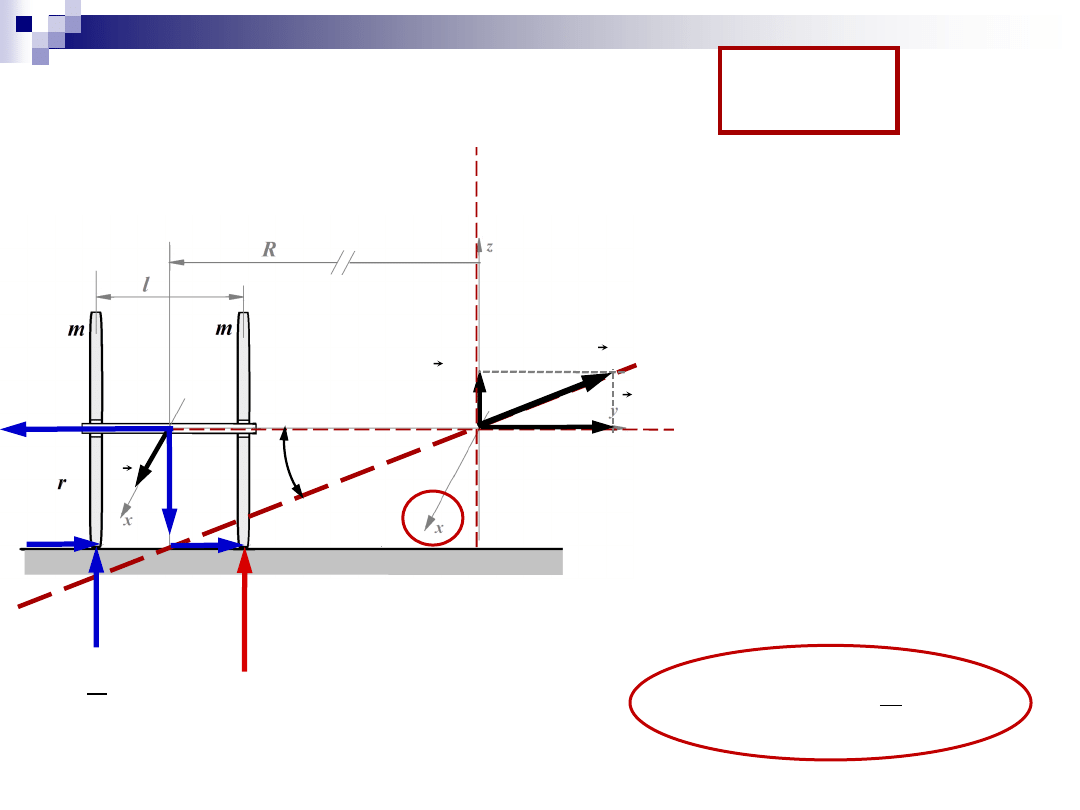
Zadanie 2

N

D

w

prec

u

1. z równoległoboku prędkości →

w

wł

oś

pre

cesji

oś obrotu

własnego

O

w

wł

w



r

wł

u

w



2. Obliczenie



)

(O

zew

M

2. obliczyć



)

(O

zew

M

(suma momentów sił zewn.
względem osi

x

)

2mg

N

A

R

A

R

D

B





)

(O

zew

M





)

( A

zew

M

l

N

D



2

2

l

mg





r

B





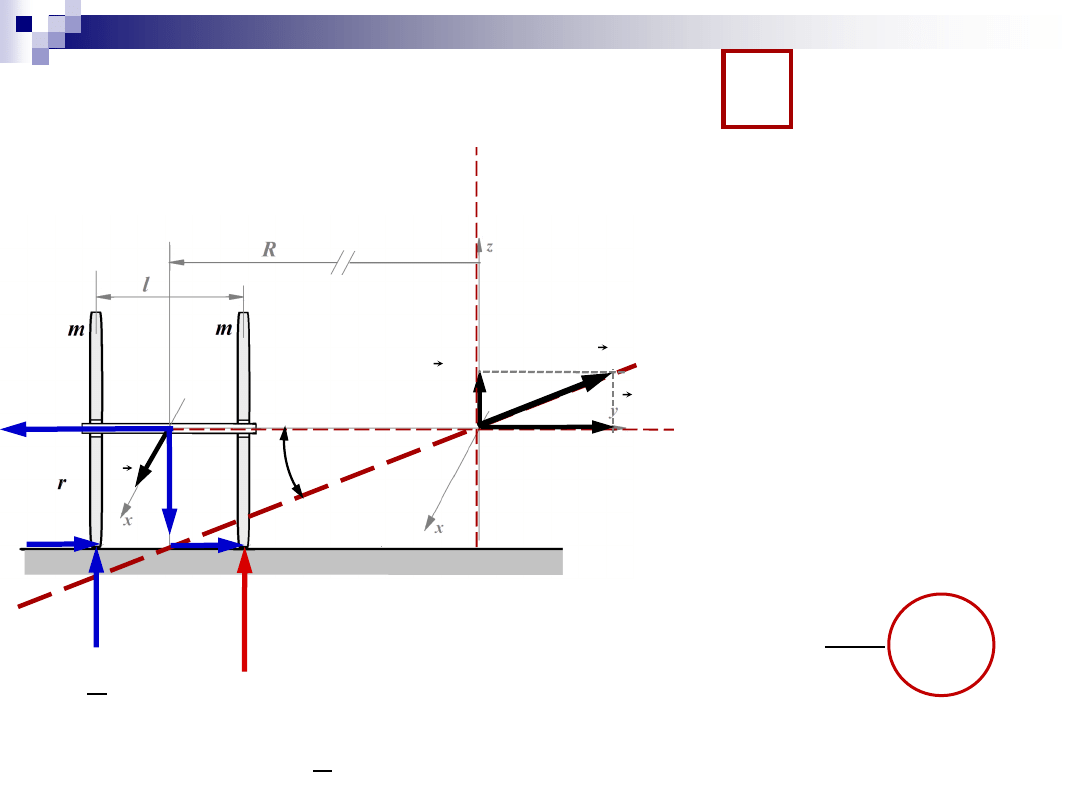
Zadanie 2

N

D

w

prec

u

1. z równoległoboku prędkości →

w

wł

oś

pre

cesji

oś obrotu

własnego

O

w

wł

w



2. obliczyć



)

(O

zew

M

(suma momentów sił zewn.
względem osi

x

)

2mg

N

A

R

A

R

D

B

r

B

l

mg

l

N

M

D

O

zew















2

2

)

(

3. Obliczenie

wł

I

3. obliczyć

wł

I

(moment bezwładności
względem osi obr. własnego y)

2

2

2

2

mr

mr

I

I

wł

y









r

wł

u

w



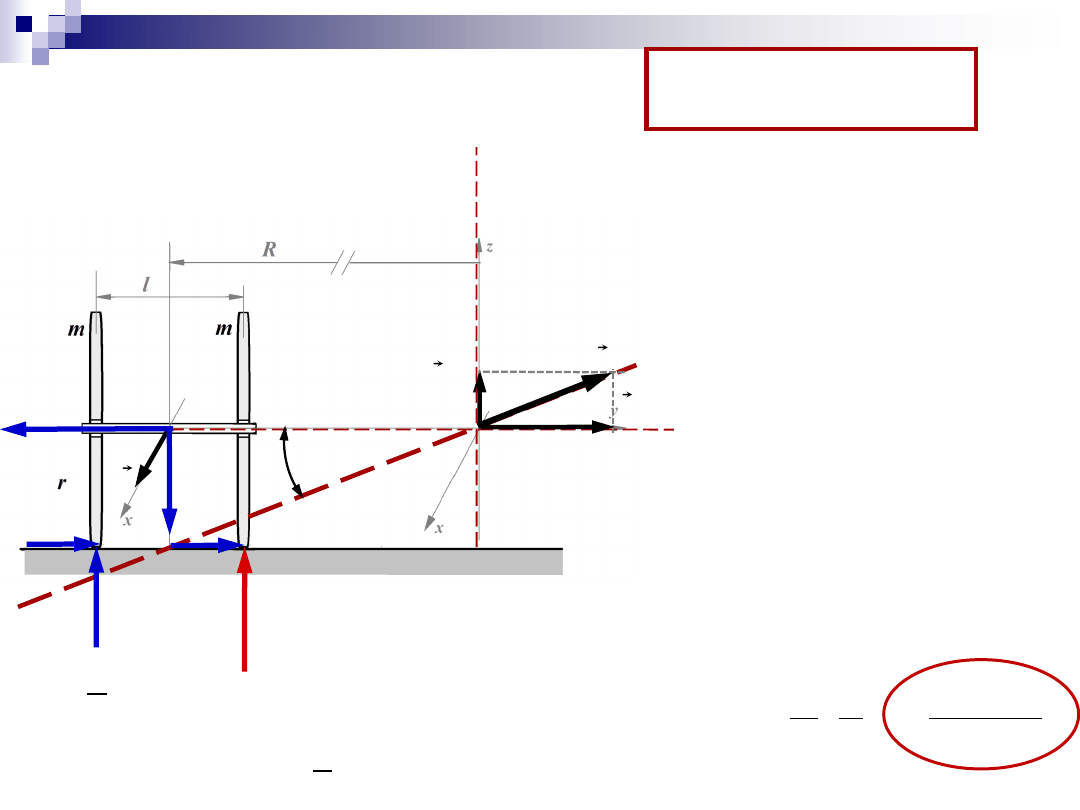
Zadanie 2

N

D

w

prec

u

1. z równoległoboku prędkości →

w

wł

oś

pre

cesji

oś obrotu

własnego

O

w

wł

w



2. obliczyć



)

(O

zew

M

(suma momentów sił zewn.
względem osi

x

)

2mg

N

A

R

A

R

D

B

3. obliczyć

wł

I

(moment bezwładności
względem osi obr. własnego y)

2

mr

I

I

wł

y





4. Obliczenie





wł

prec

wł

I

w

w









r

wł

u

w



r

B

l

mg

l

N

M

D

O

zew















2

2

)

(

4. obliczyć





wł

prec

wł

I

w

w



















wł

prec

wł

I

w

w



















90

sin

2

wł

prec

mr

w

w













 





r

R

mr

u

u

2

r

R

mr





2

2

u

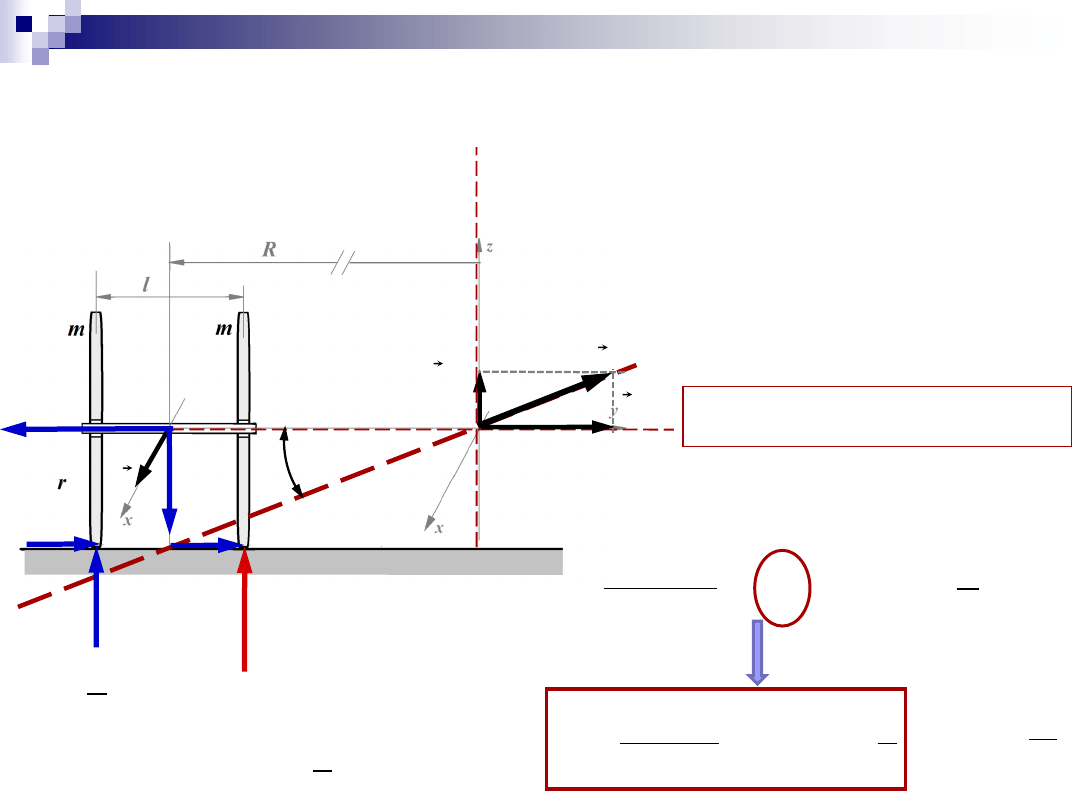
Zadanie 2

N

D

w

prec

u

1. z równoległoboku prędkości →

w

wł

oś

pre

cesji

oś obrotu

własnego

O

w

wł

w



2. obliczyć



)

(O

zew

M

(suma momentów sił zewn.
względem osi

x

)

2mg

N

A

R

A

R

D

B

3. obliczyć

wł

I

(moment bezwładności
względem osi obr. własnego y)

2

mr

I

I

wł

y





r

wł

u

w



r

B

l

mg

l

N

M

D

O

zew















2

2

)

(

4. obliczyć





wł

prec

wł

I

w

w









5. Obliczenie

N

D













)

(O

zew

wł

prec

wł

M

I

w

w





czyli:







r

R

mr

2

2

u

r

B

l

mg

l

N

D











2

2

l

r

B

mg

l

R

mr

N













2

u

gdzie:

r

m

B

2

2

u





20

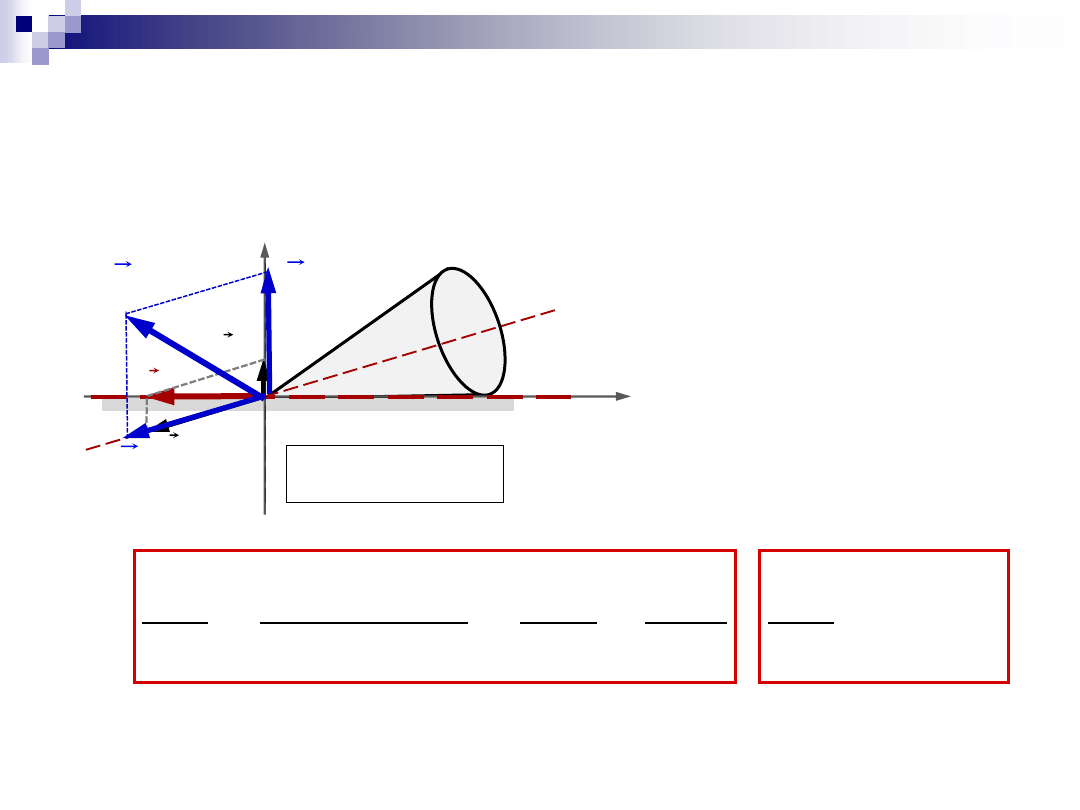
Wstęp

w

w

wł

w

prec

K

1

K

2

K

wł

prec

w

w

w











zatem:



K



prec

prec

I

w





wł

wł

I

w





2

1

K

K











Ruch kulisty – dynamika

przy czym:

zew

M

dt

K

d













dt

K

d

dt

K

d

dt

K

K

d

dt

K

d

2

1

2

1



















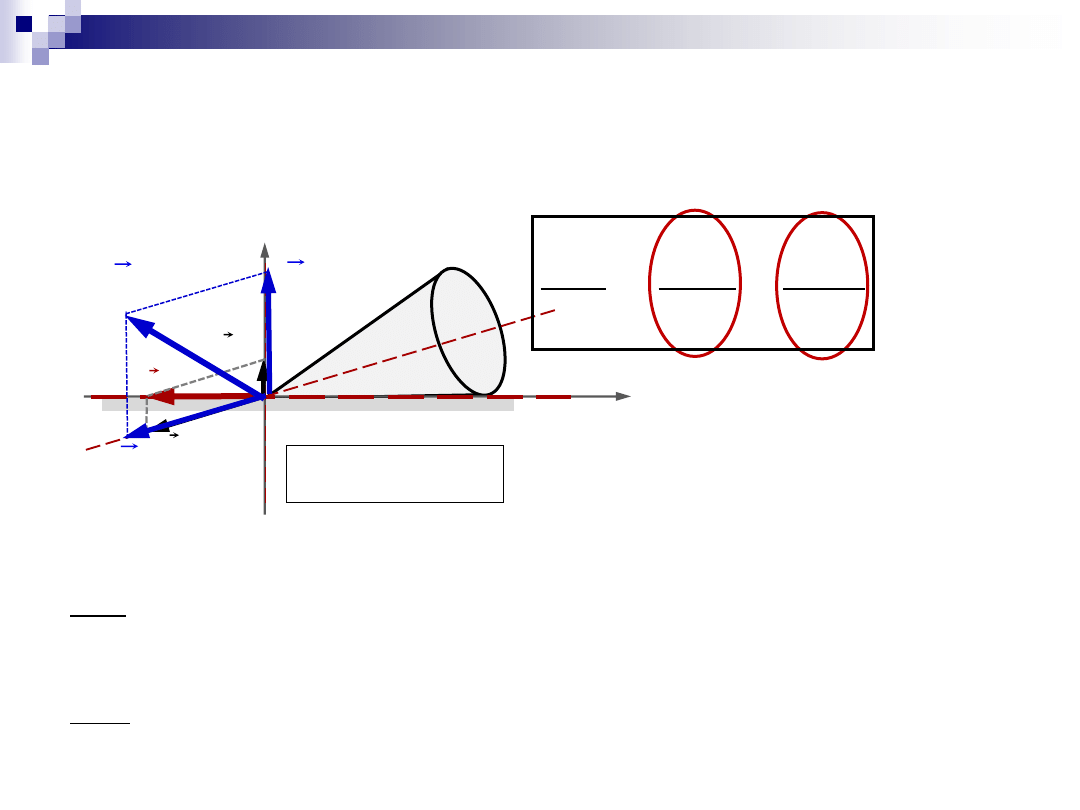
w

w

wł

w

prec

Ruch kulisty

pochodna wektora krętu

Wstęp

K

1

K

2

K

dt

K

d

dt

K

d

dt

K

d

2

1











wł

prec

w

w

w















1

1

1

1

0

K

K

K

K

wł

wł

prec

wł

prec







































w

w

w

w

w





0

2

2

2

2





















K

K

K

K

prec

wł

prec

wł

prec



















w

w

w

w

w

1

1

K

dt

K

d











w

2

2

K

dt

K

d











w

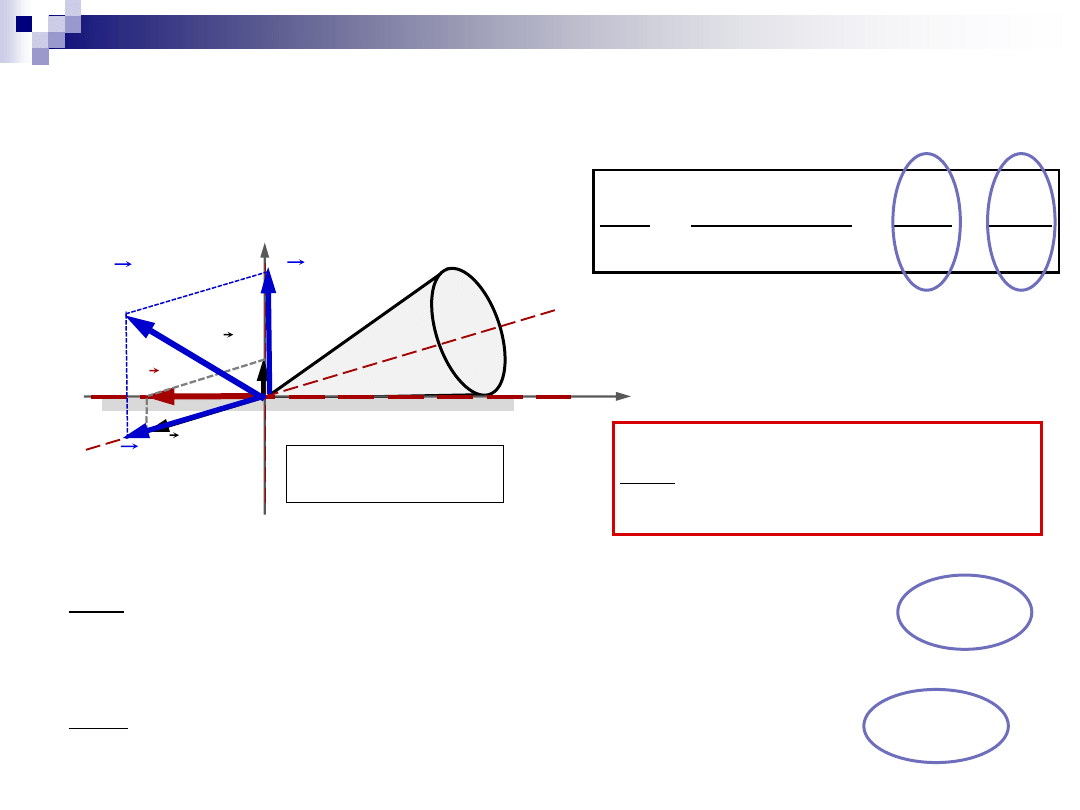
Wstęp

w

w

wł

w

prec

K

1

K

2

K

wł

prec

w

w

w















dt

K

d

dt

K

d

dt

K

K

d

dt

K

d

2

1

2

1



















Ruch kulisty – dynamika c.d.





1

1

1

1

1

1

0

K

K

K

K

K

dt

K

d

wł

wł

prec

wł

prec

















































w

w

w

w

w

w





0

2

2

2

2

2

2

























K

K

K

K

K

dt

K

d

prec

wł

prec

wł

prec

























w

w

w

w

w

w

2

1

K

K

dt

K

d

prec

wł



















w

w

zatem: