J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 12 • KMBiM WILiŚ PG
1
P
rzykłady analizy płyt – c.d.
Ćwiczenie 12
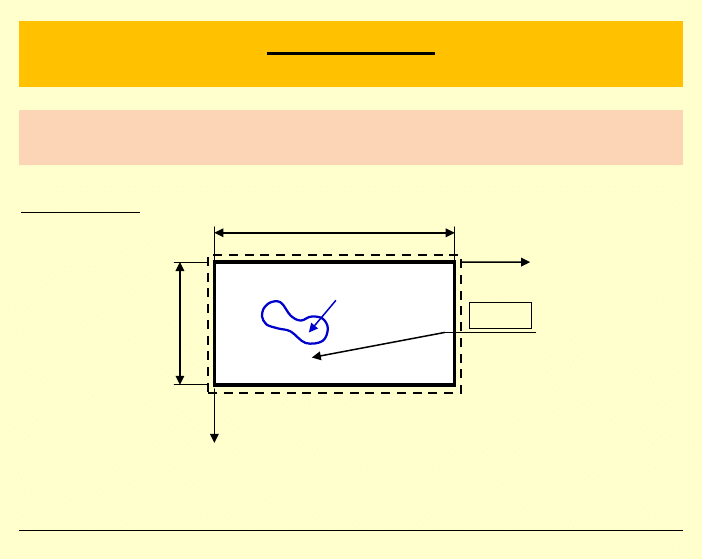
PŁYTA PROSTOKĄTNA, SWOBODNIE PODPARTA,
DOWOLNIE OBCIĄŻONA
Rzut z góry:
Przyjmujemy rozwiązanie powyższego zagadnienia za pomocą
szeregu Fouriera.
a
b
1
x
2
x
(
)
1
2
,
q x x
, ,
E
h
ν
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 12 • KMBiM WILiŚ PG
2
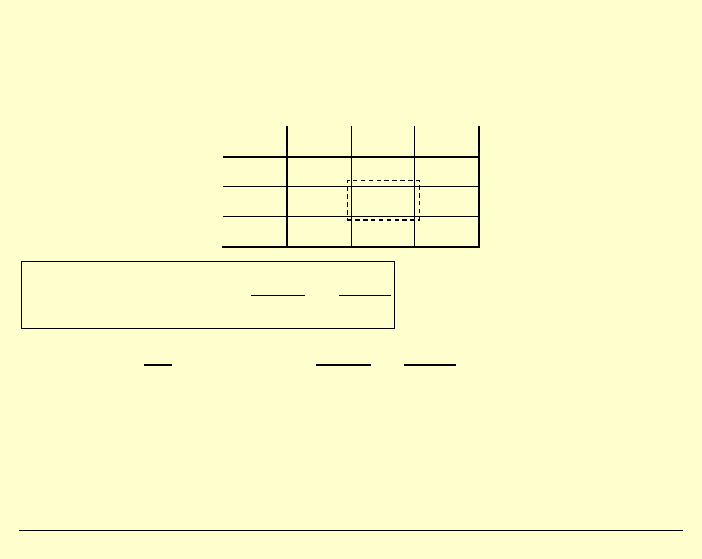
Założymy szereg sinusowy, gdyż możemy zawsze uważać
(
)
1
2
,
q x x
za funkcję nieparzystą dwóch zmiennych, zgodnie z wyobrażalnym
schematem:
a
a
a
b
+
−
+
b
−
+
−
b
+
−
+
(
)
1
2
1
2
1
1
,
sin
sin
mn
m
n
m x
n x
q x x
a
a
b
π
π
∞
∞
=
=
=
∑∑
,
gdzie:
(
)
1
2
1
2
1
2
0 0
4
,
sin
sin
a b
mn
m x
n x
a
q x x
dx dx
ab
a
b
π
π
=
∫∫
,
przy czym:
,
m n
–
liczby całkowite:
1, 2,3...
Powyższy wzór wynika z ortogonalności funkcji
( )
sin
i dowodzi
się go analogicznie jak w przypadku szeregów pojedynczych!
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 12 • KMBiM WILiŚ PG
3
(
)
1
2
0
,
q x x
q
const
=
=
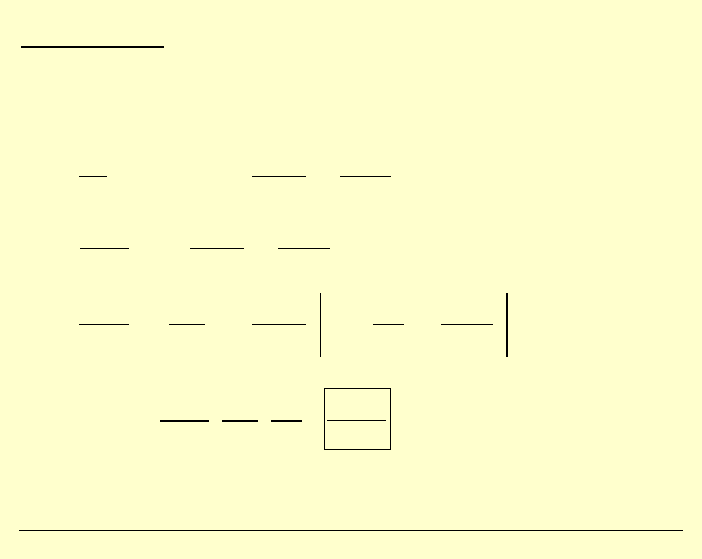
Przykładowo:
Niech:
Wówczas:
(
)
1
2
1
2
1
2
0 0
4
,
sin
sin
a b
mn
m x
n x
a
q x x
dx dx
ab
a
b
π
π
=
∫∫
0
1
2
1
2
0 0
4
sin
sin
a b
mn
q
m x
n x
a
dx dx
ab
a
b
π
π
⋅
=
∫∫
0
1
2
0
0
4
cos
cos
a
b
mn
q
m x
n x
a
b
a
ab
m
a
n
b
π
π
π
π
⋅
=
⋅ −
⋅
⋅ −
Zatem:
0
4
2
2
mn
q
a
b
a
ab
m
n
π π
⋅
=
⋅
⋅
=
0
2
16 q
mn
π
⋅
, jeżeli
m
i
n
są nieparzyste,
lub:
0
mn
a
=
, gdy
m
lub
n
jest parzyste!
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 12 • KMBiM WILiŚ PG
4
W
ogólnym przypadku obciążenia zakładamy rozwiązanie:
(
)
1
2
1
2
1
1
,
sin
sin
mn
m
n
m x
n x
w x x
w
a
b
π
π
∞
∞
=
=
=
∑∑
Funkcja ta spełnia warunki brzegowe swobodnego podparcia!
Podstawienie do równania:
(
)
(
)
0
1
2
4
1
2
,
,
q
x x
w x x
D
∇
=
daje związek:
2
2
2
mn
mn
m
n
D
w
a
a
b
π
π
⋅
+
⋅
=
czyli:
(
)
1
2
1
2
2
4
2
2
1
1
1
,
sin
sin
mn
m
n
a
m x
n x
w x x
D
a
b
m
n
a
b
π
π
π
∞
∞
=
=
=
⋅
+
∑∑
przy czym:
,
m n
–
liczby całkowite:
1, 2,3...
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 12 • KMBiM WILiŚ PG
5
Przypadek szczególny:
(
)
1
2
0
,
q x x
q
const
=
=
(
)
0
1
2
1
2
2
6
2
2
1
1
16
,
sin
sin
mn
m
n
q
a
m x
n x
w x x
D
a
b
m
n
mn
a
b
π
π
π
∞
∞
=
=
⋅
=
⋅
⋅
+
∑∑
,
gdzie:
,
m n
–
liczby całkowite nieparzyste:
1,3,5...
Maks.
ugięcie:
( )
1
2
1
0
2
6
2
2
1
1
2
1
16
2
max
2
m n
m
n
a
x
q
w
b
D
x
m
n
mn
a
b
π
+
−
∞
∞
=
=
=
−
⋅
=
⋅
=
⋅
+
∑∑
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 12 • KMBiM WILiŚ PG
6
Szereg ten jest szybkozbieżny, często wystarczy tylko pierwszy jego
wyraz (tj. dla
1
m
= ,
1
n
=
), przykładowo:
1)
Jeżeli a b
= oraz
1
m
n
= = :
4
4
0
0
6
4
max
0,00416
q a
q a
w
D
D
π
⋅ ⋅
⋅
=
=
⋅
po uwzględnieniu większej liczby wyrazów →
4
0
max
0,00406
q a
w
D
⋅
=
⋅
(wynik ścisły)
2)
Jeżeli
3
b
a
=
, to:
4
0
max
0,0122
q a
w
D
⋅
=
⋅
(wynik ścisły)
3)
Jeżeli b → ∞ (pasmo), to:
4
0
max
0,0130
q a
w
D
⋅
=
⋅
(wynik ścisły)
Wniosek: dla
3
b
a
>
obliczenia praktyczne
płyty można zastąpić
obliczeniem
pasma płytowego (dla obciążeń zbliżonych do
równomiernie rozłożonych)!
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 12 • KMBiM WILiŚ PG
7
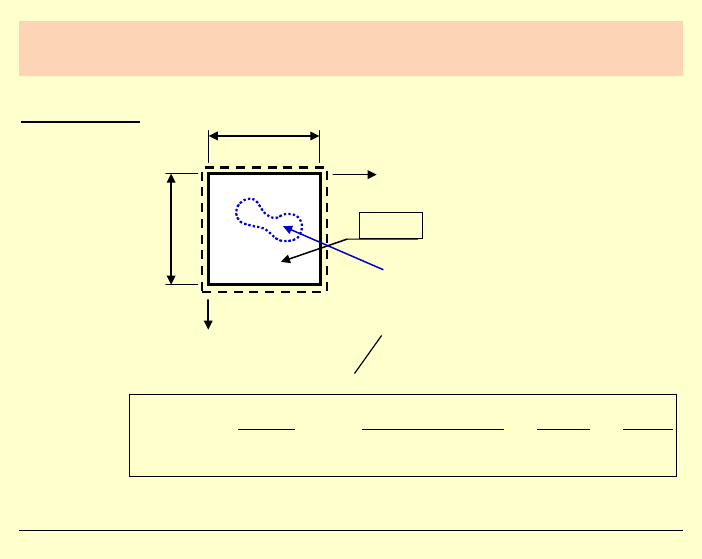
PŁYTA KWADRATOWA
– WYZNACZANIE MOMENTÓW
W PŁYCIE
1
5
ν
≈
Rzut z góry:
Przyjęto dla płyty żelbetowej:
Dla a
b
= :
(
)
(
)
4
0
1
2
1
2
2
6
2
2
1
1
16
,
sin
sin
m
n
q
m x
n x
a
w x x
D
a
a
mn m
n
π
π
π
∞
∞
=
=
⋅
=
⋅
⋅
+
∑∑
Dodatkowo, z symetrii:
(
)
(
)
11
1
2
22
1
2
,
,
M
x x
M
x x
=
;
,11
,22
w
w
=
1
x
2
x
a
a
, ,
E
h
ν
(
)
1
2
,
q x x
q
const
= =
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 12 • KMBiM WILiŚ PG
8
Moment zginający:
(
)
(
)
11
,11
,22
,11
1
M
D
w
w
D w
ν
ν
= − ⋅
+ ⋅
= − ⋅
⋅ +
(
)
2
0
1
2
,11
2
4
2
2
1
1
16
sin
sin
m
n
q a
m x
n x
m
w
D
a
a
n
m
n
π
π
π
∞
∞
=
=
⋅
= −
⋅
⋅
+
∑∑
→ dla
1
m
= ,
1
n
= i dla
1
2
x
a
=
,
2
2
x
a
=
mamy:
(
)
2
2
0
11
0
4
4
1
0,048
q a
M
q a
ν
π
⋅ ⋅
=
⋅ +
≈
⋅ ⋅
Moment
skręcający:
(
)
12
,12
1
M
D
w
ν
= − ⋅ − ⋅
(
)
2
0
1
2
,12
2
4
2
2
1
1
16
1
cos
cos
m
n
q a
m x
n x
w
D
a
a
m
n
π
π
π
∞
∞
=
=
⋅
=
⋅
+
∑∑
→ dla
1
m
= ,
1
n
= i dla
1
0
x
=
,
2
0
x
=
mamy:
(
)
2
2
0
12
0
4
4
1
0,032
q a
M
q a
ν
π
⋅ ⋅
= −
⋅ −
≈ −
⋅ ⋅
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 12 • KMBiM WILiŚ PG
9
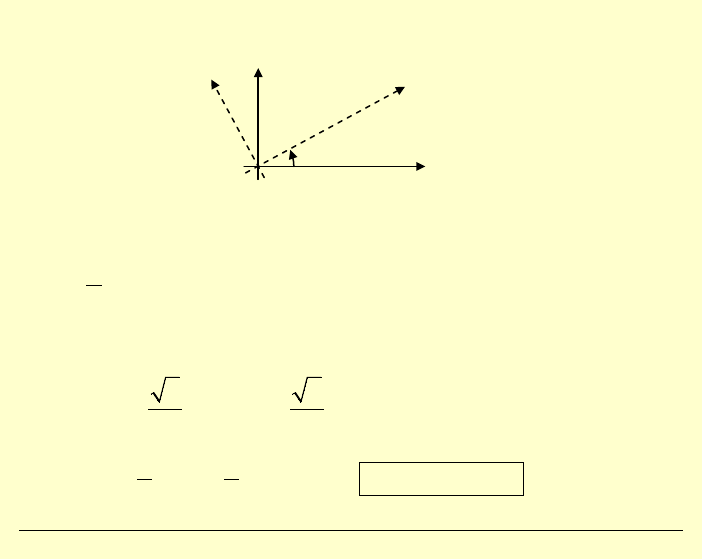
Obliczymy
moment zginający w przypadku osi obróconych o kąt
45
ϕ
=
°.
Ze wzorów transformacyjnych dla
naprężeń, wynika iż:
2
2
11
22
12
cos
sin
sin 2
nn
M
M
M
M
ϕ
ϕ
ϕ
=
⋅
+
⋅
+
⋅
(
)
22
11
12
1
sin 2
cos 2
2
ns
M
M
M
M
ϕ
ϕ
= ⋅
−
⋅
+
⋅
Zatem, dla
45
ϕ
=
°:
2
2
11
22
12
2
2
1
2
2
nn
M
M
M
M
=
⋅
+
⋅
+
⋅
11
11
12
1
1
1
2
2
nn
M
M
M
M
=
⋅ +
⋅ +
⋅
→
11
12
nn
M
M
M
=
+
1
x
2
x
s
n
ϕ
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 12 • KMBiM WILiŚ PG
10
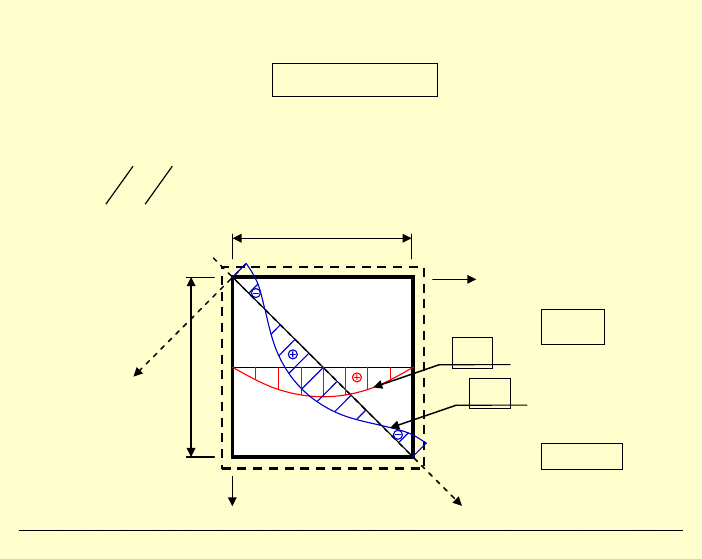
Wykresy momentów w płycie:
Jeżeli dla
45
ϕ
=
° mamy:
11
12
nn
M
M
M
=
+
to w szczególności:
→
( )
2
0
0;0
0,032
nn
M
q a
= −
⋅
→
(
)
2
0
;
0,048
2
2
nn
a
a
M
q a
=
⋅
s
n
1
x
2
x
a
a
0, 032
0, 032
0, 048
0, 048
11
M
2
0
q a
×
nn
M
0, 20
ν
=
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 12 • KMBiM WILiŚ PG
11
Dyskusja!
1)
W płycie swobodnie podpartej (obciążonej równomiernie)
występują ujemne momenty zginające w narożach!
Dlatego też w żelbecie zbroi się takie płyty w narożach również
górą
5
a
na odległościach
!
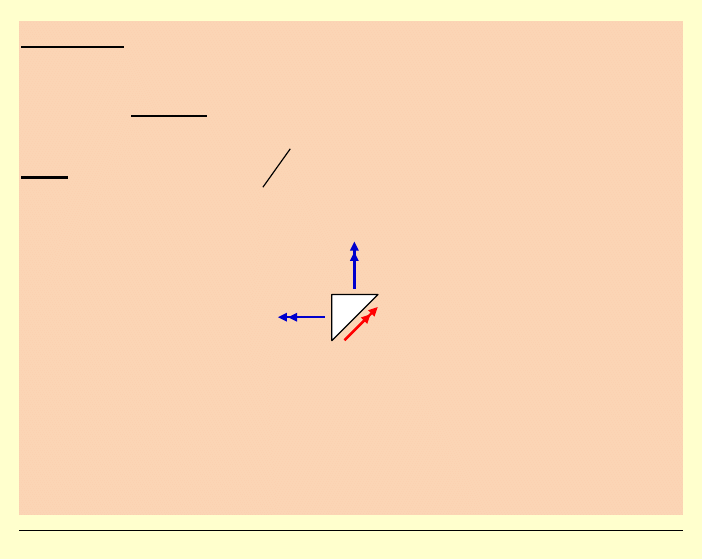
2) Sprawdzenie warunków równowagi w narożu
Jak wyjaśnić ten paradoks?
Odpowiedź: Momenty oznaczone wektorami osiowymi
są momentami skupionymi (kNm), a momenty
2
0
0,032 q a
⋅
są momentami rozłożonymi (kNm/m).
Po pomnożeniu przez długości boków trójkąta „paradoks” ten znika.
(
)
0,032 zginaj
ący
(
)
0,032 skr
ęcający
(
)
0,032 skr
ęcający
Document Outline
Wyszukiwarka
Podobne podstrony:
34) TSiP 2010 11 ćw13
25) TSiP 2010 11 ćw07
30) TSiP 2010 11 ćw09
35) TSiP 2010 11 ćw11
24) TSiP 2010 11 ćw06
31) TSiP 2010 11 ćw10
29) TSiP 2010 11 ćw08
37) TSiP 2010 11 ćw14
34) TSiP 2010 11 ćw13
25) TSiP 2010 11 ćw07
30) TSiP 2010 11 ćw09
więcej podobnych podstron